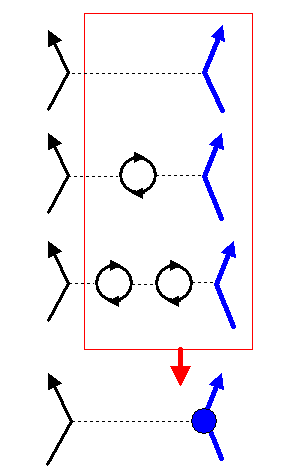
Zusammenfassung des Buchkapitels:
In der QED werden Feynmangraphen umso unwichtiger, je mehr Vertices sie enthalten, denn jeder Vertex führt zu einem Faktor \[ \sqrt{\frac{1}{137}} \approx 0,085 \] In der starken Wechselwirkung (QCD) sind die Verhältnisse leider nicht so günstig, denn die Farbladung der starken Wechselwirkung wächst bei etwas größeren Abständen auf über \(1\) an (angegeben in natürlichen Einheiten), so dass Feynmangraphen dann keinen Sinn mehr machen. Hier sind die Details dazu:
Der Grund für die Abstandsabhängigkeit einer Ladung (elektrische Ladung oder starke Farbladung) sind die virtuellen Teilchen, die sich um die Ladung herum versammeln und diese nach außen hin abschirmen oder verstärken können. In der Sprache der Feynmangraphen sieht das für die elektrische Ladung so aus:

Für relativ kleine durch das Photon übertragene Energien und
Impulse (was großen Abständen entspricht)
nimmt die elektrische Ladung einen konstanten Wert an, nämlich
\( \sqrt{1/137} \) in natürlichen
Einheiten. Man befindet sich außerhalb der abschirmenden Polarisationswolke.
Für große übertragene Impulse (was kleinen Abständen entspricht) werden dagegen die virtuellen Teilchen-Antiteilchen- Paare immer wichtiger, und die Ladung des untersuchten Objektes weicht zunehmend vom oben angegebenen Wert ab. Bei der elektromagnetischen Wechselwirkung wächst die Ladung dabei an, d.h. man taucht zunehmend in die abschirmende Polarisationswolke aus virtuellen Teilchen ein. Man spricht von der Polarisation des Vakuums – wir hatten sie bereits in Kapitel 5.1 kurz kennengelernt.
Analog ist es in der QCD, wenn ein Gluon an ein Quark ankoppelt, nur dass hier die starke Farbladung abnimmt, wenn das Gluon große Impulse überträgt. Bei geringen Gluonenergien (z.B. im Schwerpunktsystem zweier Quarks) kann man dies in eine Abstandsabhängigkeit der starken Farbladung übersetzen: Bei kleinen Abständen nimmt die starke Farbladung ab, bei großen dagegen immer weiter zu.
Dadurch nehmen die Kräfte zwischen starken Ladungen mit zunehmendem Abstand nicht ab. Die Polarisationswolke einer starken Ladung frisst sich deshalb immer weiter nach außen, was wiederum die starke Ladung verstärkt, und so fort. Letztlich würde das ganze Universum von der wuchernden Polarisationswolke erfasst. Das lässt sich nur dann vermeiden, wenn sich in der Nähe eines jeden Quarks ein oder mehrere weitere Quarks befinden, deren starke Farbladungen sich gegenseitig neutralisieren. Dies ist genau die Forderung, die wir unter dem Stichwort Confinement bereits erhoben hatten.
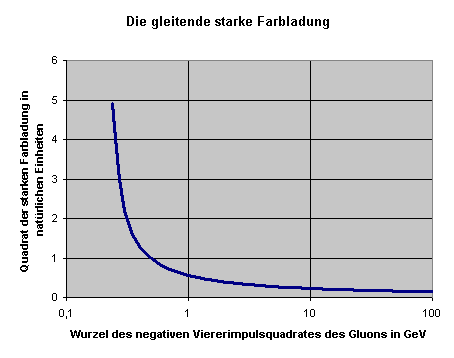
Die gleitende starke Farbladung nimmt für große negative
Viererimpulsquadrate des ankoppeden Gluons (entspricht großen Gluonimpulsen) immer weiter ab.
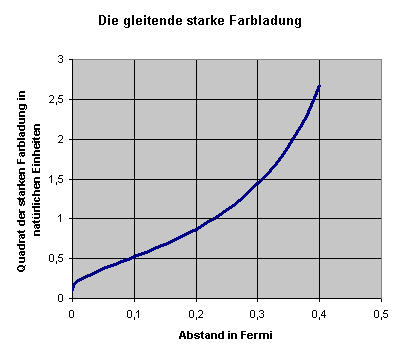
Die gleitende starke Farbladung kann
auch abhängig vom Abstand
zwischen den Quarks betrachtet werden. Sie nimmt für große Abstände
immer weiter zu.
Bei Gluonimpulsen von mehr als etwa 1 GeV ist
die starke Farbladung klein genug, so dass sich Feynmangraphen anwenden lassen.
Man sagt, die Quarks sind bei solchen Prozessen asymptotisch frei.
Das entspricht Quarkabständen unterhalb von 0,1 Fermi, also etwa einem
Zehntel des Protondurchmessers. Typische Quarkabstände in Hadronen liegen darüber, d.h.
für die Beschreibung der Quarkbindung in Hadronen eignen sich Feynmangraphen nicht oder nur eingeschränkt.
a) Formeln zur gleitenden Kopplungskonstante (Ladung) und ihrer Renormierung
(für Leser mit mathematisch-physikalischem Hintergrundwissen)
Die expliziten Formeln für die gleitenden Kopplungskonstanten (Ladungen) in der QED und QCD sind recht einfach, so dass ich sie hier kurz darstellen möchte. Nebenbei sehen wir hier ein schönes Beispiel für das Renormierungsverfahren, mit dem die Loop-Integral-Divergenzen eliminiert werden, so dass schließlich physikalisch sinnvolle Größen berechnet werden können. Letztlich hat mich u.a. dieses Beispiel dazu animiert, das Buchkapitel 6.3 über Renormierung zu schreiben.
Beginnen wir mit der QED und der gleitenden elektrischen Kopplungskonstanten (Ladung). Im Buchkapitel (und der obigen Zusammenfassung) hatten wir gesehen, dass eine Photonlinie beliebig viele Elektron-Positron-Loops enthalten kann, bevor dieses Photon an ein geladenes Teilchen ankoppelt. Das entspricht der Wolke virtueller Teilchen, die das geladene Teilchen umgibt. Natürlich sind auch noch komplexere Feynmangrafen möglich, die wir aber vernachlässigen.
Die Elektron-Positron-Loops verändern die Ladung des geladenes Teilchens (so wie dies anschaulich die Polarisationswolke tut), und zwar in Abhängigkeit vom Viererimpulsquadrat \[ q^{2} := (E/c)^{2} - \boldsymbol{p}^{2} \] des Photons. Die Rechnung (siehe z.B. Halzen, Martin: Quarks & Leptons, Kap. 7) ergibt den folgenden Zusammenhang zwischen der nackten Ladung \(e_{0}\) und der vom Photon bei dessen Viererimpulsquadrat gesehenen Ladung \( e(q^{2}) \): \[ e^{2}(q^{2}) = \] \[ = e_{0}^{2} \, \left(1 - I(q^{2}) + I^{2}(q^{2}) - \, ... \right) = \] \[ = \frac{e_{0}^{2}}{1 + I(q^{2})} \] wobei wir im letzten Schritt die geometrische Reihe in der Klammer nach der bekannten Formel zusammengefasst haben. Der Term \( - I(q^{2}) \) entspricht dabei dem Beitrag eines Elektron-Positron-Loops, der einmal, zweimal, dreimal etc. auftreten kann, was die Terme der geometrischen Reihe ergibt. Dabei ist \(I(q^{2})\) zunächst unendlich groß, da beliebig große Elektron-Positron-Impulse im Loop auftreten können, was zu einem divergenten Impulsintegral für den Loop führt.
Diese Unendlichkeit müssen wir mit Hilfe der Renormierung beseitigen (siehe auch Kapitel 6.3). Dazu lassen wir zunächst im divergenten Loop-Impulsintegral alle Impulse oberhalb eines sehr großen Viererimpulsquadrates \(M^{2}\) einfach weg (Impuls-Cut-Off), so dass sich ein endliches Integral ergibt. Später müssen wir dann den Grenzfall unendlich großer \(M^{2}\) untersuchen. Für große \(|q^{2}|\) (im Vergleich zum Quadrat der Elektron-Positron-Masse im Loop) ergibt die Rechnung in guter Näherung dann den Ausdruck \[ I(q^{2}) = \frac{\alpha_{0}}{3 \pi} \, \ln{ \frac{ M^{2} }{ |q^{2}| }} = \] \[ = - \frac{\alpha_{0}}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ M^{2} }} \] wobei wir wie üblich die Abkürzung \[ \alpha_{0} = k \frac{e_{0}^{2}}{\hbar c} \] für das (nackte) Ladungsquadrat in natürlichen Einheiten verwendet haben. Wie wir sehen, ist die Divergenz von \( I(q^{2}) \) bei wachsendem Impuls-Cut-Off \( M^{2} \) nur logarithmisch, also ziemlich mild.
Die Betragsstriche bei \( |q^{2}| \) sind deshalb notwendig, da beim Austausch virtueller Photonen zwischen Ladungen das Photon-Viererimpulsquadrat negativ ist. So überträgt im Schwerpunktsystem der Ladungen das Photon überhaupt keine Energie, so dass dort sogar \( q^{2} = - \boldsymbol{p}^{2} \) ist. Mit der Abkürzung \[ \alpha = k \frac{e^{2}}{\hbar c} \] erhalten wir damit \[ \alpha(q^{2}) = \frac{ \alpha_{0} }{ 1 + I(q^{2}) } = \] \[ = \frac{ \alpha_{0} }{ 1 - \frac{\alpha_{0}}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ M^{2} } } } = \] \[ = \frac{ 1 }{ \frac{1}{\alpha_{0}} - \frac{1}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ M^{2} } } } \] In dieser Formel treten noch das nackte Ladungsquadrat \(\alpha_{0}\) sowie der Impuls-Cut-Off \( M^{2} \) auf. Beides sind keine physikalisch sinnvollen Größen. Wir können jedoch im Sinne der Renormierung diese beiden unphysikalischen Größen eliminieren, indem wir für ein beliebiges Referenz-Viererimpulsquadrat \( \mu^{2} \) den Wert von \( \alpha(\mu^{2}) \) vorgeben (d.h. die entsprechende elektrische Ladung bei diesem Photon-Viererimpulsquadrat messen). Die entsprechende Formel \[ \alpha(\mu^{2}) = \frac{ 1 }{ \frac{1}{\alpha_{0}} - \frac{1}{3 \pi} \, \ln{ \frac{ |\mu^{2}| }{ M^{2} } } } \] stellen wir nun nach \(\alpha_{0}\) frei, was nach kurzer Rechnung die Gleichung \[ \alpha_{0} = \frac{ 1 }{ \frac{1}{\alpha(\mu^{2})} + \frac{1}{3 \pi} \, \ln{ \frac{ |\mu^{2}| }{ M^{2} } } } \] ergibt. Dies setzen wir oben in die Gleichung \[ \alpha(q^{2}) = \frac{ 1 }{ \frac{1}{\alpha_{0}} - \frac{1}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ M^{2} } } } \] ein: \[ \alpha(q^{2}) = \] \[ = \frac{ 1 }{ \frac{1}{\alpha(\mu^{2})} + \frac{1}{3 \pi} \, \ln{ \frac{ |\mu^{2}| }{ M^{2} } } - \frac{1}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ M^{2} } } } = \] \[ = \frac{ \alpha(\mu^{2}) }{ 1 + \frac{ \alpha(\mu^{2}) }{3 \pi} \, \left( \ln{ \frac{ |\mu^{2}| }{ M^{2} } } - \ln{ \frac{ |q^{2}| }{ M^{2} } } \right) } = \] \[ = \frac{\alpha(\mu^{2}) }{ 1 - \frac{\alpha(\mu^{2})}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } } \] Das ist genau die Formel für die gleitende Kopplungskonstante (elektrische Ladung) in der QED. Halten wir fest:
| gleitende elektrische Ladung (elektrische Kopplungskonstante) in der QED: \[ \alpha(q^{2}) = \frac{\alpha(\mu^{2}) }{ 1 - \frac{\alpha(\mu^{2})}{3 \pi} \, \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } } \] |
Diese Formel gilt für nicht zu kleine \(|q^{2}|\) (größer als die Elektronmasse)
und für nicht zu große \(|q^{2}|\) (denn wir haben nur eine Teilchensorte im Loop
berücksichtigt, nämlich Elektronen bzw. Positronen).
Sie enthält nur noch physikalisch sinnvolle Größen – sowohl Cut-Off als auch nackte Ladung
sind entfallen.
Dafür muss die Ladung aber bei einem beliebigen Photon-Viererimpulsquadrat \( \mu^{2} \)
einmal experimentell bestimmt werden. Sie dient dann als Aufhängepunkt (Renormierungspunkt) für die
elektrische Ladung bei anderen Photon-Viererimpulsquadraten. Die Formel bewirkt ein sehr langsames Anwachsen
der elektrischen Ladung bei höheren Photonimpulsen (kürzeren Abständen).
In der QCD (der Quantenfeldtheorie der starken Wechselwirkung)
tritt das Gluon an die Stelle des Photons, und die starke Farbladung tritt an die Stelle der
elektrischen Ladung.
Auch ein Gluon kann zwischenzeitlich ein virtuelles Teilchen-Antiteilchen-Paar hervorbringen, nämlich ein Quark-Antiquark-Paar. Im Unterschied zum Photon kann es aber auch ein weiteres Gluon außenden und wieder absorbieren. Neben Quark-Loops können also auch Gluon-Loops in einer Gluon-Linie auftreten. Diese bewirken, dass sich der Vorfaktor im Loop-Term \( I(q^{2}) \) ändert. Es ergibt sich so für die starke Kopplungskonstante die Formel
| gleitende Farbladung (starke Kopplungskonstante) in der QCD: \[ \alpha_{s}(q^{2}) = \frac{ \alpha_{s}(\mu^{2}) }{ 1 + \frac{ \alpha_{s}(\mu^{2}) }{12 \pi} \, (33 - 2 n) \, \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } } \] |
Dabei ist \( n \) die Anzahl Quark-Sorten (Flavor), die wir im Quark-Antiquark-Loop berücksichtigen.
Die Zahl \(33\) in der obigen Formel hat ihren Ursprung in den Gluon-Loops.
Da \(n\) maximal \(6\) ist, bleibt der Vorfaktor des \( \ln{} \)-Terms positiv,
im Gegensatz zur QED, wo er negativ ist.
Das führt dazu, dass die starke Kopplungskonstante für
größere Gluon-Impulsquadrate (kleinere Abstände) kleiner wird,
während es bei der elektromagnetischen Kopplungskonstante genau umgekehrt ist.
Ursache dafür sind die Gluon-Loops.
Es ist üblich, die obige Formel noch etwas umzuschreiben: \[ \alpha_{s}(q^{2}) = \frac{ \alpha_{s}(\mu^{2}) }{ 1 + \frac{ \alpha_{s}(\mu^{2}) }{12 \pi} \, (33 - 2 n) \, \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } } = \] ... wir erweitern mit \( 12 \pi / \alpha_{s}(\mu^{2}) \) \[ = \frac{ 12 \pi }{ \frac{12 \pi}{\alpha_{s}(\mu^{2})} + (33 - 2 n) \, \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } } = \] ... wir klammern im Nenner \( (33 - 2 n) \) aus \[ = \frac{ 12 \pi }{ { (33 - 2 n) \left[ \frac{12 \pi}{(33 - 2 n) \, \alpha_{s}(\mu^{2}) } + \ln{ \frac{ |q^{2}| }{ |\mu^{2}| } } \right] } } = \] ... wir fassen im Nenner alles in einem Logarithmus zusammen \[ = \frac{ 12 \pi } { { (33 - 2 n) \, \ln{ \left( e^{ \frac{12 \pi}{(33 - 2 n) \, \alpha_{s}(\mu^{2}) } } \cdot \frac{ |q^{2}| }{ |\mu^{2}| } \right) } } } = \] ... wir definieren ein passendes \(\Lambda^{2}\) \[ = \frac{ 12 \pi }{ (33 - 2 n) \, \ln{ \frac{|q^{2}|}{\Lambda^{2}} } } \] mit der Abkürzung \[ \Lambda^{2} := |\mu^{2}| \cdot e^{ - \frac{ 12 \pi }{ (33 - 2 n) \, \alpha_{s}(\mu^{2}) } } \] Wir haben also:
| gleitende Farbladung (starke Kopplungskonstante) in der QCD: \[ \alpha_{s}(q^{2}) = \frac{ 12 \pi }{ (33 - 2 n) \, \ln{ \frac{|q^{2}|}{\Lambda^{2}} } } \] |
Der Parameter \(\Lambda\) hängt ausschließlich von dem zur Renormierung
gewählten Gluon-Viererimpulsquadrat \(\mu^{2}\)
und der dort gemessenen starken Kopplung \(\alpha_{s}(\mu^{2})\) ab,
d.h. \(\Lambda\) muss experimentell bestimmt werden, wobei die Wahl des Renormierungspunktes \(\mu^{2}\)
beliebig ist. Allerdings muss
\[
|\mu^{2}| \gt \Lambda^{2}
\]
sein, denn
in der Definition von \(\Lambda^{2}\) ist der Faktor
\[
e^{ - \frac{ 12 \pi }{ (33 - 2 n) \, \alpha_{s}(\mu^{2}) } }
\]
garantiert kleiner als 1, wenn wir von maximal 6 Quarksorten ausgehen und
\[
\alpha_{s}(\mu^{2}) \lt 1
\]
voraussetzen, wie es in der Störungstheorie der Fall sein muss,
um die obige Formel überhaupt damit herleiten zu können.
Da \(\Lambda\) die physikalische Dimension eines Impulses hat und da man mit Hilfe der Lichtgeschwindigkeit \(c\) daraus eine Energie oder Masse machen kann, ist durch die Renormierung letztlich eine Energie- oder Massenskala in die QCD hineingekommen, die es in der nicht-quantisierten Theorie so nicht gibt. Renormierung führt also zur Einführung einer Massenskala in die entsprechende Quantenfeldtheorie.
Es hat sich etabliert, zur Bestimmung von \(\Lambda\) als Renormierungspunkt die Masse des Z-Bosons zu wählen: \[ \mu^{2} = m_{Z}^{2} = (91,2 \, \mathrm{GeV})^{2} \] (wir drücken alle Größen in Energieeinheiten aus und lassen entsprechend \(c\) weg). Experimentell findet man dann \[ \alpha_{s}(m_{Z}^{2}) = 0,118 \] und damit ungefähr \[ \Lambda \approx 200 \, \mathrm{MeV} \] Die obige Formel ergibt nur für Gluon-Viererimpulsquadrate oberhalb von \( \Lambda^{2} = (200 \, \mathrm{MeV})^{2} \) Sinn. Nur deutlich oberhalb dieser Skala ergeben sich Werte für \( \alpha_{s}(q^{2}) \) unterhalb von 1, d.h. nur dort können QCD-Feynmangrafen angewendet werden und nur dort ist die Formel überhaupt zuverlässig, denn sie basiert ja auf solchen Feynmangrafen. Umgekehrt kennzeichnet \(\Lambda\) die Energie-/Impuls-Skala, bei der die QCD-Störungstheorie zusammenbricht, was sich in der Formel dadurch zeigt, dass die Kopplungskonstante dort formal unendlich wird.
Die Formel basiert außerdem auf der Voraussetzung, dass das Gluon-Viererinpulsquadrat \(|q^{2}|\) deutlich größer ist als das Massenquadrat der Quarks in den Loops, denn nur dann gilt die verwendete Näherungsformel für den Loop-Term \( I(q^{2}) \). Da sowieso \[ |q^{2}| \gt \Lambda^{2} \approx (200 \, \mathrm{MeV})^{2} \] sein muss, wird man sicher die leichten 3 Quarks in den Loops berücksichtigen müssen, bei höheren Impulsen dann auch c- und b-Quarks und erst bei sehr hohen Impulsen dann das top-Quark. Für die Grafik von \( \alpha_{s}(q^{2}) \) im Buchkapitel habe ich statt dessen einfach die Formel \[ \alpha_{s}(q^{2}) = \frac{ A }{ \ln{ \frac{|q^{2}|}{\Lambda^{2}} }} \] mit \( \Lambda = 200 \, \mathrm{MeV} \)verwendet und den Vorfaktor \(A\) so angepasst, dass der Messwert \( \alpha_{s}(m_{Z}^{2}) = 0,118 \) reproduziert wird, was für \( A = 1,437 \) gut hinkommt.
Um die Impulsabhängigkeit der gleitenden Kopplungskonstanten im statischen Grenzfall in eine Abstandsabhängigkeit umzurechnen, muss man streng genommen die Fouriertransformation des Ausdrucks \[ \frac{ \alpha_{s}(\boldsymbol{p}^{2}) }{ \boldsymbol{p}^{2} } \] berechnen, die man dann in der Form \[ \frac{\alpha_{s}(r)}{r} \] schreiben kann (Coulomb-Potential mit abstandsabhängiger Ladung, siehe auch den Zusammenhang zwischen Propagator und Yukawa-Potential in den Zusatzinfos zu Kapitel 5.2). Auf diese Weise ist die Grafik für \(\alpha_{s}(r)\) oben entstanden.
Für eine grobe Abschätzung genügt es sogar, einfach den Impuls \( \boldsymbol{p} \) analog zur Wellenlängen-Formel (de Broglie) in einen entsprechenden Abstand \[ r \approx \frac{ h}{ |\boldsymbol{p}| } = \frac{ 2 \pi \hbar c }{ |\boldsymbol{p}| c } \] umzurechnen, so dass Impuls und Abstand antiproportional zueinander sind und 1 GeV ungefähr einem Abstand von 1 fm entspricht. Die Abstandsskala in der Buchgrafik wurde nach diesem Verfahren festgelegt.
Übrigens: Natürlich kann man auch die QED-Formel für die gleitende elektrische Kopplungskonstante ähnlich wie die QCD-Formel mit einem Parameter \(\Lambda\) umschreiben. Bei diesem extrem hohen Impuls \(\Lambda\) wird die elektrische Kopplungskonstante formal unendlich – man spricht vom Landau-Pol.
Letztlich bedeutet dieser Landau-Pol analog zur QCD, dass in diesem Bereich die Störungstheorie für die QED nicht mehr gilt. Allerdings dürfte in diesem hohen Energiebereich die QED sowieso längst in eine umfassendere Theorie übergehen, so dass der Landau-Pol in der Realität wohl keine Rolle spielt.
In der Fachliteratur wird die gleitende Kopplungskonstante auch oft mit Hilfe der sogenannten Betafunktion \( \beta(\alpha) \) dargestellt. Diese Funktion legt über die folgende Differentialgleichung das Verhalten der gleitenden Kopplungskonstante bei wachsendem Viererimpulsquadrat \( \lambda := |q^{2}| \) fest:
| Betafunktion und gleitende Kopplungskonstante: \[ \beta(\alpha) = \lambda \, \frac{\partial \alpha}{\partial \lambda} \] mit \[ \lambda := |q^{2}| \] |
(siehe z.B.
Wikipedia: Beta function (physics)).
Hier findet man auch oft abweichende Konventionen – so kann man statt \(\alpha\) auch dessen Wurzel,
also die Kopplungskonstante \(g\) bzw. \(e\) verwenden, oder aber statt
\(\lambda\) dessen Wurzel als Variable verwenden,
was in beiden Fällen zu einer etwas anderen Betafunktion führt; die
Differentialgleichung bleibt in beiden Fällen aber dieselbe.
Gelegentlich wird die obige Differentialgleichung auch in der Form \[ \frac{ \partial \ln{\alpha} }{ \partial \ln{ \lambda } } = \frac{ \beta(\alpha) }{ \alpha } \] geschrieben (siehe z.B. Wikipedia: Renormalization group ). Mit \[ \partial \ln{\alpha} = \frac{ \partial \alpha }{ \alpha } \] \[ \partial \ln{\lambda} = \frac{ \partial \lambda }{ \lambda } \] folgt daraus \[ \frac{\lambda}{\alpha} \, \frac{\partial \alpha}{\partial \lambda} = \frac{\beta(\alpha)}{\alpha} \] und somit unsere obige Gleichung \[ \lambda \, \frac{\partial \alpha}{\partial \lambda} = \beta(\alpha) \]
Die Differentialgleichung lässt sich leicht integrieren. Dazu schreiben wir sie in der Form \[ \frac{\partial \alpha}{\beta(\alpha)} = \frac{\partial \lambda}{\lambda} \] und integrieren von \( \lambda = |\mu^{2}| \) bis \( \lambda = |q^{2}| \), also \[ \int_{\alpha(\mu^{2})}^{ \alpha(q^{2})} \frac{d\alpha}{\beta(\alpha)} = \int_{|\mu|^{2}}^{ |q^{2}|} \frac{d\lambda}{\lambda} \] In der QED bzw. QCD hat die Betafunktion in der von uns gewählten Konvention die folgende Form:
| Betafunktion in der QED und QCD: \[ \beta(\alpha) = B \, \alpha^{2} \] |
mit einer jeweils passenden Konstante \(B\), die wir gleich noch angeben werden.
Die Stammfunktion von \[ \frac{ 1 }{ \beta(\alpha) } = \frac{1}{B} \, \alpha^{- 2} \] lautet \[ - \frac{1}{B} \, \alpha^{- 1} \] Damit können wir die obigen Integrale links und rechts ausrechnen und die Gleichung schrittweise nach \( \alpha(q^{2}) \) freistellen: \[ \frac{1}{B} \, \frac{1}{\alpha(\mu^{2})} - \frac{1}{B} \, \frac{1}{\alpha(q^{2})} = \ln{ \frac{|q^{2}|}{|\mu^{2}|} } \] ... wir multiplizieren mit \(B\) und fassen die Brüche links zusammen (gleichnamig machen) \[ \frac{ \alpha(q^{2}) - \alpha(\mu^{2}) }{ \alpha(q^{2}) \cdot \alpha(\mu^{2}) } = B \, \ln{ \frac{|q^{2}|}{|\mu^{2}|} } \] ... wir multiplizieren mit dem Nenner \[ \alpha(q^{2}) - \alpha(\mu^{2}) = \alpha(q^{2}) \, \alpha(\mu^{2}) \, B \, \ln{ \frac{|q^{2}|}{|\mu^{2}|} } \] ... Terme mit \(\alpha(q^{2})\) nach links, Rest nach rechts und dann links \(\alpha(q^{2})\) ausklammern \[ \alpha(q^{2}) \, \left( 1 - \alpha(\mu^{2}) \, B \, \ln{ \frac{|q^{2}|}{|\mu^{2}|} } \right) = \alpha(\mu^{2}) \] ... nach \(\alpha(q^{2})\) freistellen \[ \alpha(q^{2}) = \frac{ \alpha(\mu^{2}) }{ 1 - \alpha(\mu^{2}) \, B \, \ln{ \frac{|q^{2}|}{|\mu^{2}|} } } \] Die letzte Formel entspricht genau unseren obigen Formeln für die gleitende Kopplungskonstante in der QED und QCD, wobei unsere Konstante \(B\) so aussieht:
| QED: \[ B = \frac{ 1 }{3 \pi} \] QCD: \[ B = - \frac{33 - 2 n}{12 \pi} \] |
Wenn die Betafunktion \( \beta(\alpha) \) positiv ist,
so ist nach der Differentialgleichung
\[
\beta(\alpha) = \lambda \, \frac{\partial \alpha}{\partial \lambda}
\]
auch
\[
\frac{\partial \alpha}{\partial \lambda}
\]
positiv, d.h. die Kopplungskonstante \(\alpha\) wird zu hohen Impulsen \(\lambda := |q^{2}|\)
(also kleinen Abständen)
hin größer.
Das ist in der QED der Fall. In der QCD ist dagegen \(B\) und damit auch \( \beta(\alpha) \)
negativ, so dass die Kopplungskonstante \(\alpha\) zu hohen Impulsen
(kleinen Abständen) hin schwächer wird
(Stichwort asymptotische Freiheit).
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 31 January 2024