Zusammenfassung des Buchkapitels:
Bis heute wurden in den Experimenten an den großen Beschleunigern mehrere Dutzend verschiedene Teilchen entdeckt, von denen die meisten sehr kurzlebig sind und schnell in andere Teilchen zerfallen. Die Vorstellung, dass sie alle elementare Objekte sein sollen, erscheint ziemlich absurd.
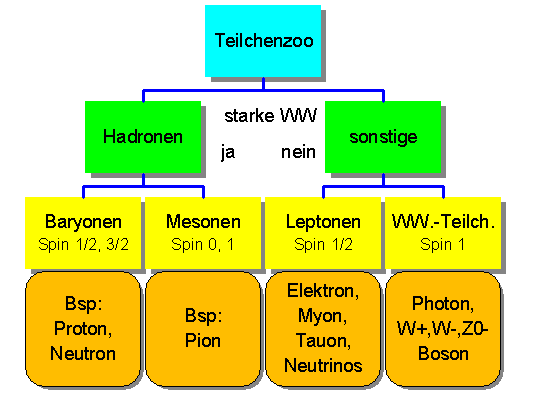
Man kann diese Teilchen in ein Ordnungsschema bringen, wobei man zur Unterscheidung die folgende Größern verwenden kann:
Nimmt man die beiden letzten Kriterien, so ergibt sich folgendes Schema:

Leptonen:
Elektron-Neutrinos können sich über die schwache Wechselwirkung nur in Elektronen verwandeln und umgekehrt,
niemals aber beispielsweise in Myonen – analog bei den anderen Neutrinos.
Entsprechend fasst man die 6 Leptonen in drei sogenannten Lepton-
Familien zusammen:
\[
\begin{pmatrix}
\nu_e \\
e
\end{pmatrix}
\;
\begin{pmatrix}
\nu_\mu \\
\mu
\end{pmatrix}
\;
\begin{pmatrix}
\nu_\tau \\
\tau
\end{pmatrix}
\]
Mehr zu Neutrinos (Massen, Neutrino-Oszillationen etc.) finden Sie in den Zusatzinfos unten.
Mehr zur Symmetrie und zu den Unterschieden
zwischen Teilchen und Antiteilchen können Sie ebenfalls in den Zusatzinfos unten finden
(CP-Verletzung, CPT-Symmetrie).
Hadronen:
Diese Teilchen spüren die starke Wechselwirkung (starke Kernkraft). Es gibt sehr viele Hadronen, wobei alle ganzzahligen Ladungswerte zwischen -2 und +2 Elementarladungen sowie alle halb- und ganzzahligen Spinwerte von 0 bis 3/2 auftreten. Hadronen mit ganzzahligem Spin (0 oder 1) nennen wir Mesonen, solche mit halbzahligem Spin (1/2 oder 3/2) Baryonen, zu denen auch Protonen und Neutronen gehören.
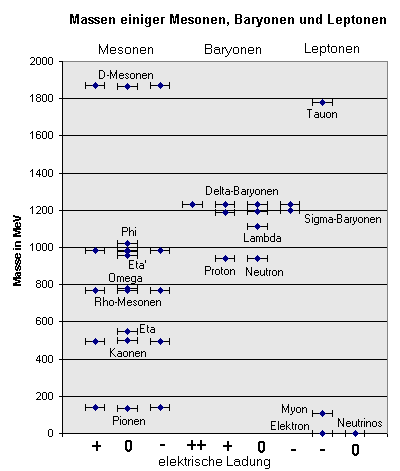
Massen einiger Mesonen, Baryonen und Leptonen
Listen wir die Fakten auf, die auf eine
innere Struktur der Hadronen hindeuten:
Es gibt sehr viele verschiedene Hadronen.
Für einige Hadronen wie das Proton, das Neutron oder das geladene Pion ist bekannt, dass sie eine Ausdehnung im Bereich von etwa einem halben bis einem Fermi besitzen.
Es fällt auf, dass Hadronen immer wieder in Gruppen mit ähnlicher Masse auftreten.
Aufgrund dieser und weiterer Fakten stellten Gell-Mann, Zweig und andere im Jahre 1964 die Hypothese auf, dass alle Hadronen aus nur wenigen Bausteinen aufgebaut seien, den sogenannten Quarks. Das Proton besteht dann aus zwei sogenannten up-Quarks (Ladung +2/3) und einem down-Quark (Ladung -1/3).

Quelle:
Wikimedia Commons File:Murray-gell-mann.jpg,
Autor Lumidek (Lubos Motl),
demnach gemeinfrei.
Bis auf den heutigen Tag ist es nicht gelungen, auch nur ein
einziges Quark als freies Teilchen in einem Detektor nachzuweisen,
und man glaubt heute, dass dies nicht möglich ist (Confinement).
Dennoch lassen sich Quarks im Inneren der Hadronen konkret nachweisen,
beispielsweise durch Beschuss mit hochenergetischen Elektronen
(ähnlich dem Rutherfordschen Streuversuch, mit die Existenz von Atomkernen im Inneren der Atome
nachgewiesen wurde, siehe Kapitel 1.3).
Wie viele verschiedene Quarks werden als Bausteine gebraucht? Zunächst nur zwei: das up- und das down-Quark (meist kurz mit den Buchstaben u und d bezeichnet). Mit ihnen lassen sich Protonen (uud) und Neutronen (udd) aufbauen. Im Lauf der Zeit wurden allerdings vier weitere Quarks entdeckt, die man strange-, charm-, bottom- und top-Quark nannte (abgekürzt: s, c, b, t). Das schwerste unter ihnen, das top- Quark, wurde erst 1995 nachgewiesen. Es ist bemerkenswert, dass sich die sechs Quarks analog zu den Leptonen in einem einfachen Schema anordnen lassen: \[ \begin{pmatrix} u \\ d \end{pmatrix} \; \begin{pmatrix} c \\ s \end{pmatrix} \; \begin{pmatrix} t \\ b \end{pmatrix} \] Man bezeichnet up, down usw. als den Flavor des Quarks. Die jeweils oben eingetragenen Quarks tragen die Ladung +2/3 (bzw. -2/3 für die entsprechenden Antiquarks), die unteren die Ladung -1/3 (bzw. +1/3 bei den Antiquarks).
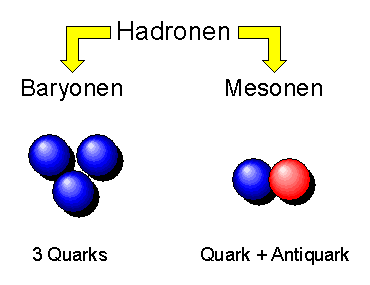
Obwohl die Ladung der Quarks drittelzahlig ist, tragen alle heute bekannten Hadronen ganzzahlige Ladungen. Wie sich herausstellt, bestehen alle Baryonen aus drei Quarks oder drei Antiquarks, alle Mesonen dagegen aus einem Quark und einem Antiquark. Dadurch ist die Ganzzahligkeit der Hadronenladung gesichert.
Um die Masse eines Quarks zu ermitteln, müsste man es ein kleines Stück frei fliegen lassen.
Es gibt aber keine freien Quarks (Confinement).
Es gibt zwei Möglichkeiten, trotzdem
dem Massenbegriff für Quarks einen gewissen Sinn zu geben.
Die erste Möglichkeit besteht darin, ganz naiv die Bindungsenergie der Quarks zu vernachlässigen und zu versuchen, die Massen der Quarks eines Hadrons gerade zu dessen Gesamtmasse aufzusummieren. Wenn man beispielsweise für die Masse der up- und down-Quarks etwa 320 MeV ansetzt, so kann man damit gut die Masse des Protons (Quarkombination u u d) und Neutrons (Quarkkombination u d d) reproduzieren. Die so gefundenen Massenwerte nennen wir Konstituenten-Quarkmassen. Das Ergebnis sieht ungefähr so aus:
| Quark | Masse in MeV |
| u,d | 320 |
| s | 500 |
| c | 1 600 |
| b | 4 800 |
| t | 170 000 |
Man kann versuchen, die Kraft zwischen den Quarks in einfachen Modellen (nichtrelativistisches Quarkmodell) zusätzlich grob abzuschätzen. Es kommt dabei heraus, dass diese Kraft im Wesentlichen konstant und damit unabhängig vom Abstand ist, auch für beliebig große Abstände. Die Quarks können sich daher niemals aus ihrer gegenseitigen Anziehung befreien, was das Confinement erklären würde.
Nun zur zweiten Möglichkeit, den Quarks eine Masse zuzuordnen:
Die starke Wechselwirkung, die die Quarks zu den Hadronen zusammenschweißt,
besitzt eine Eigenschaft, die
asymptotische Freiheit genannt wird:
Bei kleinen Abständen nimmt die sogenannte
effektive Farbladung der Quarks ab (mehr dazu im Kapitel über die gleitende Ladung).
Dann ist es möglich, das Herausschießen eines Quarks durch auftreffende Elektronen mit Hilfe der
Quantenfeldtheorie zumindest in der Anfangsphase näherungsweise zu berechnen und so
eine ungefähre Quarkmasse zu bestimmen, die
Stromquarkmasse genannt wird.
Es ergeben sich ungefähr die folgenden Werte:
| Quark | Stromquarkmasse (MeV) |
| u | 1,5 - 3,3 |
| d | 2,5 - 5 |
| s | 70 - 130 |
| c | 1 150 - 1 350 |
| b | 4 100 - 4 400 |
| t | 170 000 - 173 000 |
Das top-Quark hat dabei eine gewisse Sonderstellung, da es aufgrund seiner großen Masse fast unmittelbar nach seiner Erzeugung bereits wieder zerfällt, noch bevor es irgendein Hadron bilden kann.
Die Stromquarkmassen sind generell kleiner als die Konstituentenquarkmassen, wobei für die drei leichtesten Quarks up, down und strange dieser Unterschied ungefähr 300 MeV beträgt. Man kann sich vorstellen, dass Konstituentenquarks so etwas wie Stromquarks mit einer etwa 300 MeV bis 500 MeV schweren Hülle sind. Woraus diese Hüllen besteht, werden wir später kennenlernen.
Auf die Wechselwirkungs-Teilchen (Spin 1) gehen wir in späteren Kapiteln ein.
a) Teilchenmassen
b) Neutrino-Oszillationen
c) CP-Verletzung
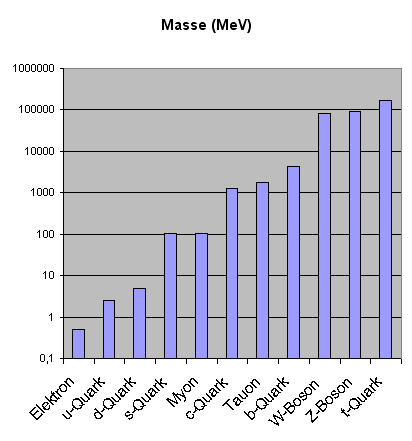
Die Massen der Quarks, Leptonen, W- und Z-Bosonen im MeV in logarithmischer Darstellung.
Man erkennt, dass sich die Teilchenmassen in allen hier dargestellten Massen-Größenordnungen
relativ gleichmäßig, aber auch fast wie zufällig verteilen.
Warum die Massen diese Werte haben, weiß heute noch niemand.
Die winzigen Neutrinomassen sind hier nicht dargestellt (da man sie nicht genau kennt und da sie
unter 2 eV liegen müssen).
Neutrino-Oszillationen werden auch in Buchkapitel 6.1 genauer besprochen. Hier sind weitere Informationen dazu:
Man kann Neutrino-Oszillationen gut mithilfe der wenigen Grundregeln zur Quantenmechanik verstehen, die in Buchkapitel 5.2 dargestellt sind. Dabei sind Neutrino-Oszillationen zugleich ein wunderbares Beispiel dafür, dass sich Quantenmechanik selbst über viele Tausend Kilometer hinweg auf physikalische Größen auswirken kann.
Bei Neutrinos gibt es (neben dem Spin) zwei verschiedene quantenmechanische Messgrößen:
Nun sind wir normalerweise gewohnt, dass die Masse bei einem Teilchen eindeutig festgelegt ist. Sie ist eine Eigenschaft, die die Teilchensorte mit bestimmt. Ein Neutron ist nun einmal schwerer als ein Proton.
Das liegt daran, dass die Teilchemasse normalerweise immer Spuren in der makroskopischen Umwelt hinterlässt, so dass sie gleichsam automatisch durch die Umwelt gemessen wird. Es gibt noch eine andere physikalische Größe, für die das zutrifft: die elektrische Ladung. Da sich diese Größen also normalerweise immer offenbaren, kann es keine quantenmechanischen Überlagerungen dieser Größen geben, denn Wahrscheinlichkeitspfeile werden nur dann addiert (überlagert, zur Interferenz gebracht), wenn die zugehörigen Messgrößen (Möglichkeiten) im betrachteten Prozess prinzipiell ununterscheidbar sind. Teilchenmasse und elektrische Ladung sind aber normalerweise immer prinzipiell unterscheidbar. Man spricht hier auch von Superauswahlregeln.
Bei den Neutrinomassen ist das anders. Neutrinos sind elektrisch neutral, hinterlassen also keine Teilchenspuren in einem Detektor. Außerdem wechselwirken sie kaum mit Materie, so dass sie nur sehr schwer nachweisbar sind. Es ist daher bis heute nicht gelungen, die Masse von Neutrinos direkt zu messen, zumal diese Masse winzig klein sein muss. Das zeigt, dass Neutrinomassen keineswegs durch die Umwelt automatisch gemessen werden, denn ein Neutrino bemerkt von dieser Umwelt meist gar nichts. Daher ist es möglich, dass quantenmechanische Überlagerungen verschiedener Neutrinomassen existieren. Es kann Wellenfunktionstabellen für Neutrinos geben, in denen Wahrscheinlichkeitspfeile für verschiedene Massen zugleich eingetragen sind.
Ähnlich ist es mit dem Neutrinoflavor: Dieser ist in dem Moment bekannt, in dem ein Neutrino zusammen mit einem geladenen Antilepton entsteht, da dieses geladene Antilepton eindeutig identifizierbar ist. Man kann Elektron, Myon und Tauon aufgrund ihrer sehr unterschiedlichen Massen leicht unterscheiden. Umgekehrt kann der Neutrinoflavor bestimmt werden, sobald das Neutrino mit Materie wechselwirkt und sich in ein geladenes Lepton umwandelt. In der Zeit zwischen der Entstehung eines Neutrinos und seiner Wechselwirkung mit Materie hinterlässt der Neutrinoflavor jedoch keine Spuren in der Umwelt. In dieser Zeit kann es also ebenfalls zu einer quantenmechanischen Überlagerungen verschiedener Neutrinoflavor kommen.
Nun wissen wir, dass zwei verschiedene quantenmechanische Messgrößen nicht unbedingt gleichzeitig messbar sein müssen. So zerstört die Impulsmessung die Kenntnis über den Teilchenort und umgekehrt. Es zeigt sich, dass auch Masse und Flavor bei Neutrinos solche komplementären Messgrößen sind, d.h. wenn man den Flavor eindeutig kennt, so hat man eine quantenmechanische Überlagerung verschiedener Massen vor sich und umgekehrt. In diesem Sinne hat ein Neutrino nicht unbedingt eine feste Masse oder einen festen Flavor. Wenn man von einem Elektron-Neutrino spricht, so meint man eine quantenmechanische Neutrinowelle im Moment ihrer Entstehung, wobei zugleich ein Anti-Elektron (Positron) entstanden sein muss.
Angenommen, unser Neutrino besitzt bei deiner Entstehung den Flavor \(\alpha\), wobei \(\alpha\) für e (Elektron), μ (Myon) oder τ (Tauon) stehen kann. Das Neutrino ist also zusammen mit einem Anti-Elektron, -Myon oder -Tauon entstanden. Dann soll \( V_{i\alpha} \) die Wahrscheinlichkeitsamplitude (der Pfeil) dafür sein, direkt nach der Entstehung die Masse \( m_{i} \) bei diesem Neutrino zu messen (auch wenn das experimentell bisher nicht möglich ist):
| \( V_{i\alpha} := \) Wahrscheinlichkeitsamplitude, bei einem Neutrino mit bekanntem Neutrinoflavor \( \alpha \) die Masse \( m_{i} \)zu messen. |
Die Wellenfunktionstabelle für ein Neutrino mit festem Flavor \(\alpha\) besteht also aus zwei
Spalten, wobei in der ersten Spalte die Massen \( m_{i} \)
und in der zweiten Spalte die Amplituden (Pfeile) \( V_{i\alpha} \)
für \(i = 1, 2, 3, \, ... \) eingetragen sind.
Oder anders ausgedrückt: \( V_{i\alpha} \) ist die Wahrscheinlichkeitsamplitude dafür, dass ein positiv geladenes W-Boson in ein geladenes Antilepton mit Flavor \(\alpha\) zerfallen ist und man bei dem dabei mit entstandenen Neutrino unmittelbar danach die Masse \(m_{i}\) misst.
Die Wahrscheinlichkeitsamplituden \( V_{i\alpha} \) sind von der Natur fest vorgegeben und hängen nur vom Flavor \(\alpha\) und der Masse \(m_{i}\) ab. Man muss ihre Werte experimentell bestimmen.
Man kann nun umgekehrt Wahrscheinlichkeitsamplituden \( U_{\alpha i} \) definieren, deren Längenquadrat die Wahrscheinlichkeit dafür angibt, bei bekannter (also gerade gemessener) Neutrinomasse \( m_{i} \) den Neutrinoflavor \(\alpha\) vorzufinden, beispielsweise durch Umwandlung des Neutrinos in ein dazu passendes geladenes Lepton. Dabei soll uns egal sein, wie wir die Messung der Neutrinomasse praktisch anstellen wollen (was schwierig sein dürfte).
| \( U_{\alpha i} := \) Wahrscheinlichkeitsamplitude, bei einem Neutrino mit bekannter Neutrinomasse \( m_{i} \) den Flavor \( \alpha \) zu messen. |
Zwischen den beiden Amplituden \( V_{i\alpha} \) und \( U_{\alpha i} \)
besteht der folgende Zusammenhang:
\[
V_{i\alpha} = U_{\alpha i}^{*}
\]
Dabei bedeutet der hochgestellte * das komplexe Konjugieren (Spiegelung des Pfeils an der x-Achse).
Die Herleitung dazu folgt etwas weiter unten.
Anmerkung:
Man kann die Amplituden \( U_{\alpha i} \) auch als die Elemente einer Matrix \(U\) auffassen, die man als Lepton-Mischungsmatrix oder auch als Pontecorvo-Maki-Nakagawa-Sakata Matrix (PMNS-Matrix) bezeichnet. Diese Matrix ist unitär und beschreibt den Basiswechsel zwischen Massen- und Flavor-Neutrinozuständen. In der gebräuchlichen Dirac-Bra-Ket-Schreibweise (siehe Die Symmetrie der Naturgesetze, Kapitel 4.5: Das mathematische Gerüst der Quantentheorie ) ist \[ U_{\alpha i} = \langle \nu_{\alpha} | \nu_{i} \rangle \] \[ V_{i \alpha} = \langle \nu_{i} | \nu_{\alpha} \rangle \] wobei \( | \nu_{i} \rangle \) ein Neutrino-Quantenzustand mit bekannter Masse \(m_i\) und \( | \nu_{\alpha} \rangle \) ein Neutrino-Quantenzustand mit bekanntem Flavor \( \alpha \) ist. Die PMNS-Matrix ist das leptonische Gegenstück zur Quark-Mischungsmatrix (Cabibbo-Kobayashi-Maskawa (CKM) -Matrix), die in Buchkapitel 6.1 angesprochen wird.
Wir wollen nun den Fall betrachten, dass ein Neutrino mit Flavor \( \alpha \) entsteht und dass wir einige Zeit später in der Entfernung \(L\), die das Neutrino bis dahin zurückgelegt hat, den (evtl. anderen) Neutrinoflavor \( \beta \) bei ihm messen. Genau das wäre dann eine Neutrino-Oszillation. Die entsprechende Wahrscheinlichkeitsamplitude nennen wir \[ A_{\beta\alpha}(L) \] Um diese Amplitude zu berechnen, zerlegen wir den Vorgang in einzelne ununterscheidbare Möglichkeiten (pro Neutrinomasse eine), die jeweils aus den folgenden drei Teilschritten bestehen:
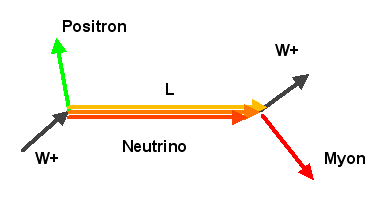
Aus Kapitel 5.2 wissen wir, dass wie pro Neutrinomasse
die Wahrscheinlichkeitsamplitude für alle Schritte zusammen
erhalten, indem wir die Amplituden der Teilschritte miteinander multiplizieren:
\[
U_{\beta i} \, e^{- i \varphi_{i}} \, V_{i\alpha}
\]
Da wir die Neutrinomasse \( m_{i} \) in diesem Beispiel nicht messen können,
da sie in diesem Setup keine im Prinzip messbaren Spuren in der physikalischen Welt hinterlassen
(weil das Neutrino hier nicht mit Materie wechselwirkt), entsprechen die verschiedenen
Neutrinomassen ununterscheidbaren Möglichkeiten, genauso wie im Doppelspaltversuch
der Durchgang durch den linken oder rechten Spalt zwei ununterscheidbare Möglichkeiten
darstellen. Wir müssen also die Wahrscheinlichkeitsamplituden dieser Massen-Möglichkeiten addieren,
um die Gesamtamplitude zu ermitteln
(mehr dazu siehe auch in Die Symmetrie der Naturgesetze,
Kapitel 4.5: Das mathematische Gerüst der Quantentheorie ):
| Wahrscheinlichkeitsamplitude dafür, dass ein Neutrino mit Flavor \(\alpha\) entstanden ist und dass wir einige Zeit später in der Entfernung \(L\) bei diesem Neutrino den Neutrinoflavor \(\beta\) messen: \[ A_{\beta\alpha}(L) = \sum_{i} U_{\beta i} \, e^{- i \varphi_{i}} \, V_{i\alpha} \] |
Bevor wir uns näher mit Schritt 2 (also dem Term \( e^{- i \varphi_{i}} \))
befassen, wollen wir uns noch kurz den Fall ansehen, bei dem
Schritt 2 einfach wegfällt.
Wir betrachten also die Wahrscheinlichkeitsamplitude \[ A_{\beta \alpha}(L=0) \] dafür, bei einem neu entstandenen Neutrino mit bekanntem Neutrinoflavor \( \alpha \) unmittelbar nach seiner Entstehung am Entstehungsort den Neutrinoflavor \( \beta \) zu messen. Die entsprechende Wahrscheinlichkeit muss gleich Eins sein, wenn \( \alpha = \beta \) ist, und Null sonst, denn wir kennen ja den Neutrinoflavor bereits. Wir wollen den willkürlichen Drehwinkel (die Phase) der entsprechenden Wahrscheinlichkeitsamplitude so wählen, dass der Pfeil nach rechts zeigt, die Amplitude also reell ist. Die Amplitude ist also \[ A_{\beta \alpha}(L=0) = \delta_{\beta \alpha} \] wobei rechts das Kroneckersymbol steht, also \( \delta_{\beta \alpha} = 1 \) für \( \alpha = \beta \) und Null sonst. Damit haben wir die Gleichung \[ A_{\beta \alpha}(L=0) = \] \[ = \sum_{i} U_{\beta i} \, V_{i\alpha} = \delta_{\beta\alpha} \] Andererseits muss die Summe der Wahrscheinlichkeiten für die einzelnen Massenwerte in Schritt 1 gleich Eins sein, denn irgendeinen Massenwert findet man garantiert. Die entsprechende Wahrscheinlichkeit für die Masse \( m_{i} \) ist durch das Längenquadrat der Amplitude \( V_{i\alpha} \) gegeben, d.h. es muss gelten: \[ \sum_{i} |V_{i\alpha}|^{2} = 1 = \sum_{i} V_{i\alpha}^{*} \, V_{i\alpha} \] wobei wir rechts \( |V_{i\alpha}|^{2} = V_{i\alpha}^{*} \, V_{i\alpha} \) verwendet haben; dabei bedeutet der hochgestellte * das komplexe Konjugieren (Spiegelung des Pfeils an der x-Achse).
Wenn wir in der Beziehung \[ \sum_{i} U_{\beta i} \, V_{i \alpha} = \delta_{\beta\alpha} \] die Flavor gleich wählen, so ergibt sich \[ \sum_{i} U_{\alpha i} \, V_{i\alpha} = 1 \] was zusammen mit der Formel \( 1 = \sum_{i} V_{i\alpha}^{*} \, V_{i\alpha} \) von oben dann \[ \sum_{i} V_{i \alpha}^{*} \, V_{i \alpha} = \sum_{i} U_{\alpha i} \, V_{i \alpha} \] ergibt. Analog kann man auch die Beziehung \[ \sum_{\alpha} U_{\alpha i}^{*} \, U_{\alpha i} = \sum_{\alpha} V_{i\alpha} \, U_{\alpha i} \] herleiten, bei der die verschiedenen Neutrinoflavor die ununterscheidbaren Möglichkeiten bilden. Man kann sich überlegen, dass aus diesen Formeln die bereits oben erwähnte Beziehung
| \[ V_{i\alpha} = U_{\alpha i}^{*} \] |
folgt.
Zurück zu unserem Fall inklusive Schritt 2, bei dem das Neutrino die Strecke \(L\) zurücklegt. Wir stellen uns dazu vor, dass wir die Fortbewegung des Neutrinos durch ein Wellenpaket beschreiben können, das in der Zeit \(t\) die Strecke \(L\) zurücklegt, wobei das Wellenpaket viel kleiner als \(L\) und viel größer als die Wellenlänge der Neutrinos sein soll. Daher umfasst das Wellenpaket immer noch viele Wellenberge und wir können es näherungsweise innerhalb seiner Ausdehnung durch eine ebene Welle beschreiben.
Das bedeutet, dass die jeweilige Wahrscheinlichkeitsamplitude zur Masse \( m_{i} \) zur Zeit \(t\) am Ort \(L\) um den Faktor \[ e^{- i \varphi_{i}} = e^{- \frac{i}{\hbar} \, (E_{i} \, t - p_{i} \, L)} \] gegenüber der Amplitude am Entstehungsort zur Zeit Null gedreht wird. Der Drehwinkel beträgt also \[ \varphi_{i} = \frac{i}{\hbar} \, (E_{i} \, t - p_{i} \, L) \] im Uhrzeigersinn. Dabei ist \[ E_{i} = \sqrt{ (m_{i} \, c^{2})^{2} + (p_{i} \, c)^{2}} \] die Energie und \( p_{i} \) der Impulsbetrag des Neutrinos. Allgemein können \(E_{i}\) und \(p_{i}\) für die verschiedenen Massenanteile des Neutrinos unterschiedlich sein, da sie die Energie-Impulserhaltung bei der Entstehung des Neutrinos (z.B. aus einem Pion) erfüllen müssen und zudem noch über die Masse \(m_{i}\) zusammenhängen.
Das Betragsquadrat der Amplitude \( A_{\beta\alpha}(L) \) hängt nur von den Differenzen der einzelnen Drehwinkel \( \varphi_{i} \) relativ zueinander ab. Das sieht man, wenn man für ein beliebiges festes \(j\) den Faktor \( e^{- i \varphi_{j}} \) aus der Summe herauszieht (wobei wir ab sofort \( V_{i\alpha} = U_{\alpha i}^{*} \) einsetzen): \[ A_{\beta \alpha}(L) = \] \[ = \sum_{i} U_{\beta i} \, e^{- i \varphi_{i}} \, V_{i\alpha} = \] \[ = \sum_{i} U_{\beta i} \, e^{- i \varphi_{i}} \, U_{\alpha i}^{*} = \] \[ = e^{- i \varphi_{j}} \, \sum_{i} \, U_{\beta i} \, e^{- i (\varphi_{i} - \varphi_{j})} \, U_{\alpha i}^{*} \] Betrachtet man die Wahrscheinlichkeit (bildet also das Betragsquadrat dieser Amplitude), so fällt der Vorfaktor \( e^{- i \varphi_{j}} \) einfach weg. Da er für den betrachteten Prozess auch sonst keine Rolle spielt, lassen wir ihn ab sofort generell weg und schreiben \[ A_{\beta\alpha}(L) = \sum_{i} U_{\beta i} \, e^{- i (\varphi_{i} - \varphi_{j})} \, U_{\alpha i}^{*} \] Berechnen wir nun konkret die Differenz der beiden Drehwinkel: \[ \varphi_{i} - \varphi_{j} = \] \[ \frac{1}{\hbar} \, (E_{i} \, t - p_{i} \, L) - \frac{1}{\hbar} \, (E_{j} \, t - p_{j} \, L) = \] \[ = \frac{1}{\hbar} \, \left[ (E_{i} - E_{j}) t - (p_{i} - p_{j}) L \right] = \] Für die Geschwindigkeit \(v\) eines Teilchens mit Impuls \(p\) und Energie \(E\) gilt nun die relativistische Formel \[ v = c^{2} \frac{p}{E} \] (folgt direkt aus \( p = m \gamma v \) und \( E = m \gamma c^{2} \), was \( p = E v / c^{2} \) ergibt, siehe Kapitel 3.2).
Für die Geschwindigkeit des Wellenpaketes setzen wir in dieser Formel statt \(p\) den Mittelwert \( (p_{i} + p_{j})/2 \) und statt \(E\) den Mittelwert \( (E_{i} + E_{j})/2 \) ein, was vollkommen ausreicht, da sich aufgrund der geringen Neutrinomasse die einzelnen Impuls- und Energiewerte nur minimal unterscheiden. Wir verwenden also \[ v = c^{2} \frac{p_{i} + p_{j}}{E_{i} + E_{j}} \] In der Formel für \( \varphi_{i} - \varphi_{j} \) ersetzen wir damit \(t\) durch \[ t = \frac{L}{v} = \frac{L}{c^{2}} \, \frac{E_{i} + E_{j}}{p_{i} + p_{j}} \] Damit erhalten wir für die Differenz der Drehwinkel: \[ \varphi_{i} - \varphi_{j} = \] \[ = \frac{1}{\hbar} \, \left[ (E_{i} - E_{j}) t - (p_{i} - p_{j}) L \right] = \] \[ = \frac{1}{\hbar} \, \left[ (E_{i} - E_{j}) \frac{L}{c^{2}} \, \frac{E_{i} + E_{j}}{p_{i} + p_{j}} - (p_{i} - p_{j}) L \right] = \] \[ = \frac{L}{\hbar c^{2}} \, \frac{1}{p_{i} + p_{j}} \, \cdot\] \[ \cdot \, \left[ (E_{i} - E_{j}) \, (E_{i} + E_{j}) - (p_{i} - p_{j}) \, (p_{i} + p_{j}) \, c^{2} \right] = \] \[ = \frac{L}{\hbar c^{2}} \, \frac{1}{p_{i} + p_{j}} \, \cdot\] \[ \cdot \, \left[ (E_{i}^{2} - E_{j}^{2}) - (p_{i}^{2} - p_{j}^{2}) c^{2} \right] = \] \[ = \frac{L}{\hbar c^{2}} \, \frac{1}{p_{i} + p_{j}} \, \cdot\] \[ \cdot \, \left[ \left( E_{i}^{2} - (p_{i} \, c)^{2} \right) - \left( E_{j}^{2} - (p_{j} \, c)^{2} \right) \right] = \] \[ = \frac{L}{\hbar c^{2}} \, \frac{1}{p_{i} + p_{j}} \, \left[ (m_{i} \, c^{2})^{2} - (m_{j} \, c^{2})^{2} \right] \] Für die Impulse \(p_{i}\) und \(p_{j}\) reicht es in diesem Ausdruck vollkommen aus, sie gleich der mittleren Neutrinoenergie \(E\) (durch \(c\)) zu setzen, da die winzige Neutrinomasse dabei wörtlich nicht ins Gewicht fällt: \[ \varphi_{i} - \varphi_{j} = \] \[ = \frac{L}{\hbar c^{2}} \, \frac{c}{2E} \, \left[ (m_{i} \, c^{2})^{2} - (m_{j} \, c^{2})^{2} \right] = \] \[ = \frac{c^{3}}{\hbar} \, L \, \frac{m_{i}^{2} - m_{j}^{2}}{2E} \] Damit ergibt sich unter Weglassen der irrelevanten Phase \( e^{- i \varphi_{j}} \):
| \[ A_{\beta\alpha}(L) = \sum_{i} U_{\beta i} \, e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{i}^{2} - m_{j}^{2}}{2E} } \, U_{\alpha i}^{*} \] |
Wie man sieht, geht hier die Differenz \( m_{i}^{2} - m_{j}^{2} \) der Neutrino-Massenquadrate ein. Genau diese Größe lässt sich aus Neutrinooszillationen also bestimmen, nicht jedoch die Neutrinomassen selbst.
Wie viele verschiedene Massen \( m_{i} \) können nun auftreten?
Gäbe es bei drei Neutrinoflavor vier verschiedene Massen (d.h. \(i\) könnte die Werte 1 bis 4 annehmen), so hätte eine Wellenfunktionstabelle mit den Massen als Messwerte vier Amplituden, eine Wellenfunktionstabelle mit den Flavorwerten als Messwerte dagegen nur drei Amplituden.
Wenn wir davon ausgehen, dass die vier Massen-Amplituden das Neutrino quantenmechanisch (bis auf Impuls und Spin) vollständig beschreiben, dann kann die alternative Beschreibung durch nur drei Flavor-Amplituden nicht vollständig sein. Für eine vollständige Beschreibung wäre ein vierter Neutrinoflavor notwendig.
Man hat am LEP-Beschleuniger aber nur drei Neutrinoflavor gefunden (siehe Kapitel 6.2), d.h. dieser vierte Flavor müsste entweder zu einem noch unbekannten geladenen Lepton passen, oder aber ein solcher Neutrinoflavor dürfte nicht durch W- und Z-Bosonen (also durch die bekannte schwache Wechselwirkung) erzeugbar sein. Man spricht auch von einem sterilen Neutrino. Wir wollen diese denkbare Möglichkeit hier außer Acht lassen und von drei verschiedenen Massen ausgehen. Nur so ist gewährleistet, dass sowohl die 3 Flavor als auch die 3 Massen zwei gleichwertige Möglichkeiten darstellen, ein Neutrino quantenmechanisch zu beschreiben (so wie wir auch Ort und Impuls als zwei gleichwertige Alternativen für eine Wellenfunktion nutzen können).
zwei Neutrinoflavor:
Betrachten wir ein einfaches Beispiel, bei dem wir uns auf nur zwei Neutrinoflavor (nehmen wir konkret e und μ) und zwei Massen \(m_{1}\) und \(m_{2}\) beschränken (es könnten aber genausogut zwei andere Massen oder Flavor sein). Wo diese Einschränkung auf zwei Massen und zwei Flavor sinnvoll ist, werden wir weiter unten noch sehen. Ein Beispiel sind Myon- und Tau-Neutrinos bei relativ kurzen Strecken \(L\) im Bereich bis zu einigen tausend Kilometern (z.B. in der Erdatmosphäre oder zwischen einem Beschleuniger und einem Detektor).
Wir können die Werte für die Wahrscheinlichkeitsamplituden \( U_{\alpha i} \) in eine 2-mal-2-Tabelle eintragen. Man kann sich überlegen, dass man bei zwei Massen und zwei Flavorn die Einträge reell wählen kann, so dass \( U_{\alpha i}^{*} = U_{\alpha i} \) ist. Außerdem muss dann \[ A_{\beta \alpha}(L=0) = \] \[ = \sum_{i} U_{\beta i} \, U_{\alpha i} = \delta_{\beta\alpha} \] gelten (siehe oben), d.h. die durch die beiden Zeilen (Index \(i\)) definierten Spaltenvektoren müssen den Betrag Eins haben und sie müssen senkrecht aufeinander stehen, so dass sie insgesamt durch eine Drehung aus den Einheitsvektoren entstanden sein müssen. Also kann man sie durch einen Drehwinkel \(\theta\) parametrisieren (analog zum Cabibbo-Winkel für Quarks). Die Tabelle und damit die Matrix \(U = (U_{\alpha i}) \) sieht dann so aus:
| \(m_{1}\) | \(m_{2}\) | |
| e | \(\cos{ \theta }\) | \(\sin{ \theta }\) |
| μ | \(- \sin{ \theta }\) | \(\cos{ \theta }\) |
Damit können wir nun \( A_{\beta\alpha}(L) \) für zwei Flavor und zwei Massen ausrechnen,
wobei wir \(j=1\) wählen:
\[
A_{\beta\alpha}(L) =
\]
\[
= \sum_{i}
U_{\beta i} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{i}^{2} - m_{j}^{2}}{2E} }
\, U_{\alpha i}^*
=
\]
\[
=
U_{\beta 1} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{1}^{2} - m_{1}^{2}}{2E} }
\, U_{\alpha 1} \, +
\]
\[
+ \,
U_{\beta 2} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\, U_{\alpha 2}
=
\]
\[
=
U_{\beta 1} \, U_{\alpha1}
+
U_{\beta 2} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\, U_{\alpha 2}
\]
Konkret haben wir also:
\[
A_{ee}(L)
=
(\cos{\theta})^{2} +
\]
\[
+
(\sin{\theta})^{2} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\]
\[
A_{\mu \mu}(L)
=
(\sin{ \theta })^{2} +
\]
\[
+
(\cos{ \theta })^{2} \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\]
\[
A_{\mu e}(L)
=
- \sin{ \theta } \, \cos{ \theta } +
\]
\[
+
\sin{ \theta } \, \cos{ \theta } \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\]
\[
A_{e \mu}(L)
=
- \sin{ \theta } \, \cos{ \theta } +
\]
\[
+
\sin{ \theta } \, \cos{ \theta } \,
e^{- i \, \frac{c^{3}}{\hbar} \, L \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} }
\]
Wie wir sehen, ist
\[
A_{\mu e}(L) = A_{e \mu}(L)
\]
Die Formeln für das Betragsquadrat ersparen wir uns hier.
Es ergibt sich dabei, dass
\[
|A_{ee}(L)|^{2} = |A_{\mu\mu}(L)|^{2}
\]
ist.
Immer wenn der Drehwinkel in der Exponentialfunktion gleich
Null ist, so dass die Exponentialfunktion gleich 1 wird,
so ergibt sich
\[
A_{ee}(L) = A_{\mu\mu}(L) = 1
\]
\[
A_{e\mu}(L) = A_{\mu e}(L) = 0
\]
Das sind genau die Abstände, bei denen der ursprüngliche Neutrinoflavor komplett wiederhergestellt ist.
Ist dagegen der Drehwinkel in der Exponentialfunktion gleich 180 Grad,
so dass die Exponentialfunktion gleich
\( - 1 \) wird,
so haben wir
\[
A_{ee}(L) = - A_{\mu\mu}(L) =
\]
\[
= (\cos{ \theta })^{2} - (\sin{ \theta })^{2} = \cos{(2 \theta)}
\]
\[
A_{\mu e}(L) = A_{e\mu}(L) =
\]
\[
= - 2 \, \sin{ \theta } \, \cos{ \theta } = - \sin{(2 \theta)}
\]
Das sind genau die Stellen, bei denen der jeweils andere Neutrinoflavor mit maximaler Wahrscheinlichkeit vorkommt,
wobei diese Wahrscheinlichkeit gleich \( (\sin{(2 \theta)})^{2} \) ist, so dass sich der
Mischungswinkel \(\theta\) daraus ermitteln lässt. Die Wahrscheinlichkeit für das Auftreten des anderen
Neutrinoflavors oszilliert also zwischen Null und \( (\sin{(2 \theta)})^{2} \)
hin und her, je nach Abstand \(L\) vom Entstehungsort des Neutrinos.
Das sieht dann folgendermaßen aus:
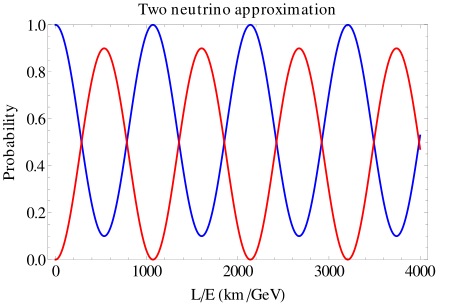
Auf der x-Achse ist das Verhältnis \(L/E\) in km/GeV angegeben.
Quelle:
Wikimedia Commons File:Oscillations two neutrino.svg, dort Public Domain.
Die Oszillation ist dann am ausgeprägtesten, wenn
\( (\sin{(2 \theta)})^{2} = 1 \)
ist,
also wenn der Mischungswinkel \(\theta\) genau 45 Grad beträgt.
Das entspricht der maximal möglichen Mischung, d.h. jede Masse trägt dann 50 % zu jedem Flavor bei.
Die Wellenlänge \(L = \lambda\) der 2-Massen-Flavoroszillation ist durch die Bedingung \[ \frac{c^{3}}{\hbar} \, \lambda \, \frac{m_{2}^{2} - m_{1}^{2}}{2E} = 2 \pi \] gegeben, d.h. \[ \lambda = \frac{2 \pi \hbar}{c^{3}} \, \frac{2E}{m_{2}^{2} - m_{1}^{2}} = \] \[ = \frac{h}{c^{3}} \, \frac{2E}{m_{2}^{2} - m_{1}^{2}} \] Die Oszillations-Wellenlänge wird also umso größer, je größer die Neutrinoenergie und je kleiner die Differenz der Massenquadrate ist. Anders ausgedrückt: Die Oszillation erfolgt umso schneller, je kleiner die Neutrinoenergie und je größer die Differenz der Massenquadrate ist. Nahe beieinander liegende Neutrinomassen ergeben eine langsame Oszillation, deutlich unterschiedliche Neutrinomassen ergeben eine schnellere Oszillation.
Eine nützliche physikalische Analogie dazu sind zwei Pendel, die durch eine Feder miteinander gekoppelt sind (gekoppelte Pendel, siehe Wikipedia: Gekoppelte Pendel), wobei die Schwingungsenergie jedes Pendels für die Wahrscheinlichkeit eines Neutrinoflavors steht.
Erzeugt man zu Beginn einen bestimmten Neutrinoflavor, so entspricht das dem Anstoßen eines der Pendel. Am Anfang schwingt dann nur dieses Pendel (man misst also nur diesen Neutrinoflavor), aber nach und nach geht die Schwingung auf das andere Pendel über, wobei dieser Übergang nur dann vollständig erfolgt, falls die beiden Pendel gleich lang sind (d.h. falls die Mischung zwischen Flavorn und Massen maximal ist, was einem Mischungswinkel \(\theta\) von 45 Grad entspricht). Man spricht auch von einer Schwebung. Je stärker die Feder zwischen den Pendeln ist, umso schneller erfolgt der Übergang.
Die Stärke der Feder entspricht also der Differenz der Massenquadrate, während jede Neutrinomasse selbst der Frequenz einer sogenannten Normalschwingung entspricht. Bei zwei Pendeln gibt es zwei solche Normalschwingungen: die entgegengesetzte Schwingung und die parallele Schwingung der beiden Pendel.
Bei der parallelen Schwingung spielt die Feder zwischen den Pendeln keine Rolle, bei der entgegengesetzten Schwingung dagegen schon. Daher ist die Frequenzen der entgegengesetzten Schwingung größer als die der parallelen Schwingung, und zwar umso mehr, je stärker die Feder ist. Hier einige Grafiken dazu (Quelle: Wikipedia: Gekoppelte Pendel, Wikimedia Commons File:Gleichsinnig.svg, File:Gegensinnig.svg, File:Schwebungsfall.svg, Urheber: Daniel Schaal Farbing, Bilder dort gemeinfrei):



Bei unterschiedlich langen Pendeln ist die Auslenkung des langen Pendels bei der parallelen Schwingung größer, bei der entgegengesetzten Schwingung dagegen kleiner als die des kürzeren Pendels. Stößt man nur eines der Pendel an (erzeugt also einen Neutrinoflavor), so regt man damit eine Überlagerung der beiden Normalschwingungen an, was einer Überlagerung von zwei Neutrinomassen entspricht. Mehr zu diesem Vergleich siehe unter Wikipedia: Neutrino oscillation sowie unter CERN Courier: Neutrinos with a swing (May 28, 1999).
drei Neutrinoflavor:
Kommen wir nun zu dem realen Fall mit drei Neutrinoflavorn und drei Neutrinomassen. Die entsprechenden Formeln nach geeigneter Parametrisierung der Mischungsamplituden \( U_{\alpha i} \) durch Drehwinkel und Phasen sind komplexer und wir wollen hier nicht im Detail auf sie eingehen. Aber auch ohne diese Formeln kann man anhand der Pendelanalogie gut verstehen, was vor sich geht, wenn man ungefähr weiß, wie groß die Differenzen der Massenquadrate sind. Die experimentellen Werte dazu lauten: \[ m_{2}^{2} - m_{1}^{2} = 7,42 \cdot 10^{- 5} \, \mathrm{eV}^{2} \] \[ m_{3}^{2} - \frac{m_1^2 + m_2^2}{2} = \pm 2,5 \cdot 10^{- 3} \, \mathrm{eV}^{2} \] Die Massenunterschiede sind also winzig (und die Massen selbst wohl auch), wobei zwei der Massen (\(m_1\) und \(m_2\)) deutlich dichter zusammenliegen als beide zur Masse \(m_3\) liegen. Meist geht man oben vom positiven Vorzeichen aus, vermutet also, dass \(m_3\) die deutlich größre Masse ist.
Die Mischung zwischen Flavorn und Massen sieht qualitativ so aus, dass das Elektron-Neutrino einen großen \(m_{1}\)-Anteil (mehr als 50 %), einen geringeren \(m_{2}\)-Anteil (ca. 25 %) und kaum oder gar keinen \(m_{3}\)-Anteil besitzt. Myon- und Tauon-Neutrino teilen die restlichen Anteile etwa gleich untereinander auf, was einer nahezu maximalen Mischung zwischen Myon- und Tauon-Neutrino entspricht.
Diese starke Mischung steht im Gegensatz zu der nur relativ schwachen Mischung bei den Quarks, bei denen die stärkste Mischung (d und s-Quark) nur bei etwa 23 Prozent liegt, entsprechend einem Cabibbo-Winkel von ungefähr 13 Grad (Stichwort CKM-Matrix, siehe Buchkapitel 6.1). Die folgende Grafik stellt diese Zusammenhänge anschaulich dar:
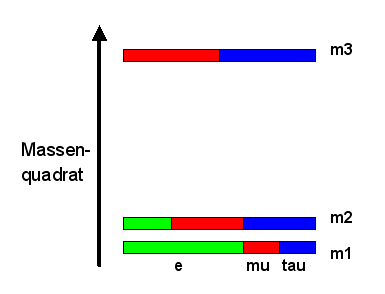
Wie sehen die einzelnen Oszillationen konkret aus?
Hier einige Grafiken aus Wikipedia:
Neutrino oscillation dazu:
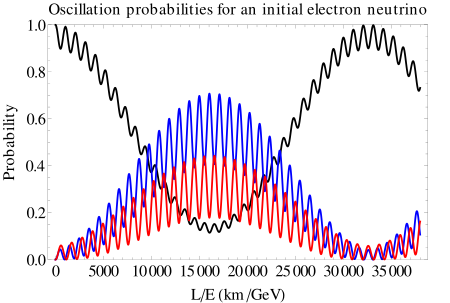
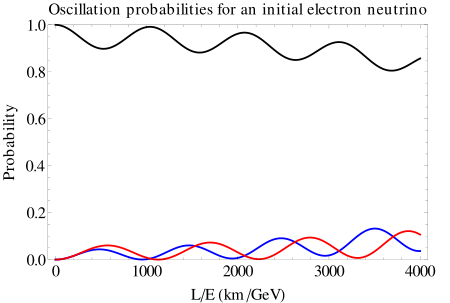
Oszillation der Neutrinoflavor bei einem neu entstandenen Elektron-Neutrino (schwarz).
Erst über lange Strecken wächst die Wahrscheinlichkeit deutlich an, ein Myon-Neutrino (blau)
oder ein Tau-Neutrino (rot) zu messen (erstes Bild).
Bei kurzen Strecken (bis einige 100 km) spielen sie dagegen kaum eine Rolle (zweites Bild).
Quelle: Wikipedia
File:Oscillations electron long.svg,
File:Oscillations electron short.svg.
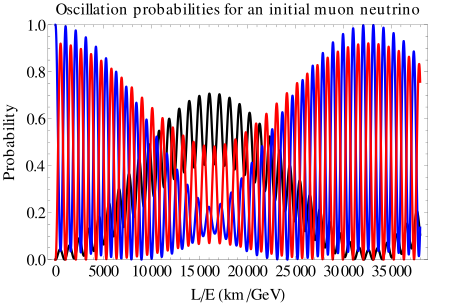
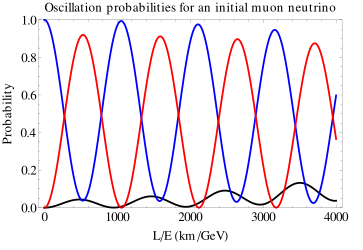
Oszillation der Neutrinoflavor bei einem neu entstandenen Myon-Neutrino (blau).
Erst über lange Strecken wächst die Wahrscheinlichkeit für Elektron-Neutrinos (schwarz)
deutlich an (erstes Bild).
Bei kurzen Strecken (bis einige 100 km) spielen sie dagegen kaum eine
Rolle und es kommt zu einer heftigen Oszillation
zwischen Myon- und Tau-Neutrinos (rot) (zweites Bild).
Das Bild für intiale Tau-Neutrinos sieht ganz ähnlich aus.
Quelle: Wikipedia
File:Oscillations muon long.svg,
File:Oscillations muon short.svg.
Man kann sich diese Oszillationen recht gut
mithilfe gekoppelter Pendel veranschaulichen.
Dabei haben wir drei Pendel (für jeden Flavor eines).
Myon- und Tauon-Neutrinopendel sind ungefähr gleich lang,
was der starken Mischung zwischen den beiden Flavorn und den
Massen \(m_{2}\) und \(m_{3}\) entspricht. Das Elektron-Neutrinopendel ist dagegen länger.
Da Myon- und Tauon-Neutrino in sehr ähnlicher Weise zu den drei Massen gemischt sind, macht es Sinn, auch den Pendelaufbau symmetrisch zu wählen. Wir bringen daher die drei Pendel in einer Linie in gleichem Abstand zueinander an, wobei sich das Elektron-Neutrinopendel in der Mitte befinden soll. Zwischen Myon- und Tauon-Neutrinopendel spannen wir eine relativ starke Feder, während wir das Elektron-Neutrinopendel mit zwei schwachen Federn zwischen diese beiden äußeren Pendel einspannen. Dabei soll die Feder zwischen Myon- und Tauon-Neutrinoopendel etwa 30 mal stärker sein als die Federn zwischen Elektron- und Myon- bzw. Tauon-Neutrinopendel.
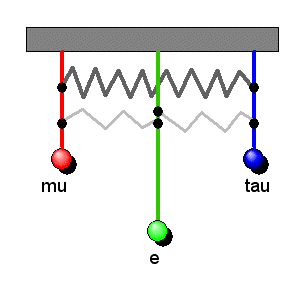
Wenn wir nun das mittlere Elektron-Neutrinopendel anstoßen,
so schwingt zunächst nur dieses Pendel stark, während
sich die beiden anderen Pendel anfangs kaum bewegen. Im Laufe der
Zeit überträgt die schwache Feder die Schwingungsenergie
fast vollständig auf das Myon- und Tauon-Neutrinopendel, die nun stark schwingen.
Später wird diese Schwingungsenergie dann wieder auf das
Elektron-Neutrinopendel zurückübertragen usw..
Aus Sicht des Elektron-Neutrinopendels verhalten sich bei längeren Zeiten die beiden anderen Pendel bezüglich der Schwingungsenergie fast wie ein einziges Pendel, da sie mit einer starken Feder eng gekoppelt sind. Daher kann man in relativ guter Näherung bei der Betrachtung solarer Elektron-Neutrinos und weiter Strecken die beiden anderen Neutrinoflavor zu einem einzigen Flavor zusammenfassen und die einfacheren Oszillationsformeln für zwei Flavor und zwei Massen verwenden. Aus der Zeitdauer, die für die Übertragung der Schwingungsenergie zwischen Elektron-Neutrinopendel und dem anderen Pendelpaar notwendig ist, lässt sich die Stärke der schwächeren Federn ermitteln, also die Massendifferenz \( m_{2}^{2} - m_{1}^{2} \).
Wenn wir dagegen das Myon-Neutrinopendel anstoßen, so wirkt sich die starke Feder zum Tauon-Neutrinopendel unmittelbar aus und die Schwingungsenergie wird relativ schnell fast komplett auf das Tauon-Neutrinopendel und wieder zurück auf das Myon-Neutrinopendel übertragen, während das Elektron-Neutrinopendel aufgrund seiner nur schwachen Federkopplung zunächst kaum eine Rolle spielt. Bei Myon-Neutrinos kann man also für kurze Entfernungen wieder gut die einfacheren Oszillationsformeln für zwei Flavor und zwei Massen verwenden, indem man das Elektron-Neutrino ignoriert. Das funktioniert beispielsweise für die in der oberen Atmosphäre erzeugten Myon-Neutrinos. Entsprechend kann man bei diesen Neutrinos die Kraft der stärkeren Feder ermitteln, also die Massendifferenz \( m_{3}^{2} - m_{1}^{2} \), die ungefähr genauso groß wie \( m_{3}^{2} - m_{2}^{2} \) ist.
Man kann die Analogie mithilfe der Normalschwingungen sogar noch etwas weiter treiben, wobei wir analog zu oben die Normalschwingungen direkt mit den Neutrinomassen identifizieren können (je größer die Neutrinomasse ist, umso höher ist die Frequenz der Normalschwingung).
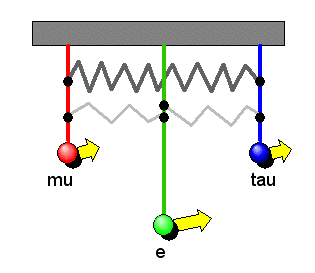
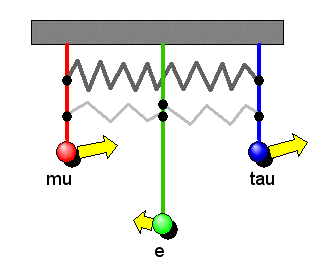
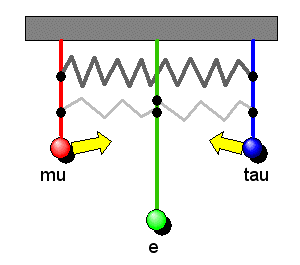
Dieses Bild gibt sogar korrekt wieder, dass das Elektron-Neutrino
überhaupt nicht mit der Masse \(m_{3}\) gemischt ist,
denn bei der \(m_{3}\)-Normalschwingung schwingt das Elektron-Neutrinopendel gar nicht.
Bei der synchronen \(m_{1}\)-Schwingung schlägt das längere
Elektron-Neutrinopendel dagegen stärker
aus als die beiden anderen Pendel, was zu dem großen Anteil des Elektron-Neutrinos zur Masse \(m_{1}\) passt.
Bei der \(m_{2}\)-Schwingung schlagen ungekehrt die beiden kürzeren Pendel (Myon- und Tauon-Neutrinos)
stärker aus, was sich ebenfalls in deren Beiträgen zeigt.
Das Bild der gekoppelten Pendel liefert also eine sehr weitgehende und nützliche Analogie, die erst an ihre
Grenzen stößt, wenn komplexe Phasen in der Mischungsmatrix \(U\) wichtig werden.
Neutrino-Experimente:
Zum Abschluss ist hier noch eine kurze Übersicht über einige aktuelle und vergangene Neutrino-Experimente:

Quelle:
Wikimedia Commons File:OPERA-Experiment-Nov2005.jpg,
Credit: Mhier, CC BY-SA 3.0 DEED

Quelle:
Wikimedia Commons File:MINOS complete.jpg,
dort Public Domain.

Quelle:
Wikimedia Commons File:IceCube drill camp 2009.jpg,
Urheber: Amble, CC BY-SA 3.0 DEED
In Buchkapitel 6.1 wird im Rahmen der schwachen Wechselwirkung neben der Paritätsverletzung auch die CP-Verletzung angesprochen. Da die Zusatzinformationen dort bereits recht umfangreich sind, habe ich weitere Informationen dazu an dieser Stelle bereitgestellt.
Die schwache Wechselwirkung verletzt die Paritätssymmetrie (P-Symmetrie), d.h. ein physikalisches Experiment und sein Spiegelbild liefern unterschiedliche Ergebnisse. Die schwache Wechselwirkung bevorzugt Quarks und Leptonen mit negativer Helizität, also mit einem Spin, der entgegen der Flugrichtung orientiert ist. Klassisch dreht sich ein solches Teilchen in Flugrichtung gesehen links herum. Diese Bevorzugung ist umso stärker, je schneller das Teilchen ist. Bei den nahezu masselosen Neutrinos wurden bisher nur negative Helizitäten beobachtet – man spricht von linkshändigen Neutrinos.
Bei Antiteilchen ist die Situation genau umgekehrt – so findet man nur rechtshändige Antineutrinos. Wenn man nun ein Experiment durch sein Spiegelbild ersetzt (also alle Helizitäten umdreht) und zusätzlich alle Teilchen durch die entsprechenden Antiteilchen ersetzt, so liegt die Vermutung nahe, dass dieses neue Experiment dieselben Wahrscheinlichkeiten (Zerfallsraten etc.) ergibt wie das ursprüngliche Experiment. Diese Vermutung bezeichnet man als CP-Symmetrie, wobei C für Charge Conjugation (Ladungsumkehr) und P für Parität (Spiegelung) steht. Die CP-Symmetrie sagt aus, dass sich Materie und Antimaterie identisch verhalten, wenn man zusätzlich alle nicht-spiegelsymmetrischen Größen (Spins, Drehimpulse etc.) umdreht.
In der Natur findet man, dass die CP-Symmetrie zwar relativ gut, aber nicht immer exakt gilt. Es gibt bei bestimmten seltenen Prozessen kleine Unterschiede zwischen Materie und Antimaterie, und die braucht man auch, da man ansonsten nicht verstehen kann, warum im heutigen Universum nur Materie und keine Antimaterie existiert. Hier ein Beispiel (siehe z.B. Particle Data Group: C.Amsler et. al: CP violation in meson decays (Januar 2010), http://pdg.lbl.gov, S. 1):
Übrigens kann man ein \(K_{L}\)-Meson nicht unmittelbar erzeugen, sondern es wird zunächst beispielsweise über die starke Wechselwirkungs-Reaktion \[ \pi^{-} + p \; \rightarrow \; K^{0} + \Lambda \] ein \(K^{0}\)-Meson oder über die Reaktion \[ \pi^{+} + p \; \rightarrow \; K^{+} + \bar{K}^{0} + p \] ein \( \bar{K}^{0} \)-Meson erzeugt.
Beide Mesonen sind elektrisch neutral, unterscheiden sich aber durch ihre Quark-Zusammensetzung, so dass sie sich bezüglich der starken Wechselwirkung unterschiedlich verhalten. Dabei ist \( K^{0} = (d \bar{s}) \) das Antiteilchen von \( \bar{K}^{0} = (\bar{d} s) \).
Letztlich ist es vollkommen analog zu den Neutrinos oben: Ein Elektron-Neutrino erkennt man am gleichzeitig erzeugten Positron, und ein \(K^{0}\)-Meson beispielsweise am gleichzeitig erzeugten \(\Lambda\). Und wie bei den Neutrinos sind auch die erzeugten \(K^{0}\) und \(\bar{K}^{0}\)-Mesonen keine Zustände mit eindeutig festgelegter Masse, sondern aufgrund der schwachen Wechselwirkung quantenmechanische Überlagerungen von zwei Zuständen, die definierte Massen und Zerfallszeiten besitzen.
Dabei wird die Masse zwar weitgehend durch die starke Wechselwirkung erzeugt, aber die schwache Wechselwirkung sorgt für winzige Massenunterschiede (etwa \( 3,5 \cdot 10^{-6} \) eV), die allerdings bei K-Mesonmassen von etwa 500 MeV kaum eine Rolle spielen.
Wichtiger ist die schwache Wechselwirkung für die Zerfallszeiten, da das \(K^{0}\) und \(\bar{K}^{0}\)-Meson aufgrund des enthaltenen \(s\)- bzw. \(\bar{s}\)-Quarks nicht über die starke Wechselwirkung zerfallen können (denn diese kann das \(s\)- und \(\bar{s}\)-Quark nicht in andere leichtere Quarks umwandeln).
Dabei nennt man den langlebigeren Zustand \(K_{L}\) (mittlere Lebesdauer \(5,1 \cdot 10^{-8}\) s) und den kurzlebigeren Zustand \(K_{S}\) (mittlere Lebesdauer \(9 \cdot 10^{-11}\) s, also fast 600 mal kleiner), wobei \(K_{L}\) die etwas größere Masse besitzt.
Ein \(K^{0}\)-Meson besteht jeweils etwa zur Hälfte aus diesen beiden Zuständen, ebenso das \(\bar{K}^{0}\)-Meson. Wenn man nun einen Strahl aus \(K^{0}\) oder \(\bar{K}^{0}\)-Mesonen erzeugt und ihn eine genügend lange Strecke fliegen lässt, so zerfällt der kurzlebige \(K_{S}\)-Anteil recht schnell und es bleibt praktisch nur noch der langlebige \(K_{L}\)-Anteil übrig.
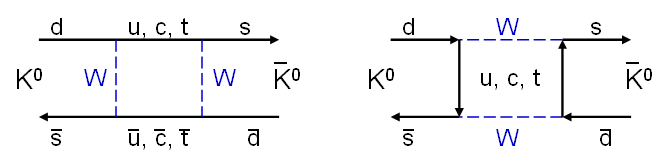
Ein \(K^{0}\)-Meson (jeweils links) kann sich über die schwache Wechselwirkung
in ein \(\bar{K}^{0}\)-Meson (jeweils rechts) umwandeln und umgekehrt.
Zu der entsprechende Wahrscheinlichkeitsamplitude tragen die oben
dargestellten Feynmangraphen bei, die man auch Box-Diagramme nennt (sie sind hier von links nach rechts zu lesen,
d.h. links steht der Anfangszustand und rechts der Endzustand).
Hier die Details:
Die obigen Feynmandiagramme zeigen: Ein \(K^{0}\)-Meson kann sich über die schwache Wechselwirkung in ein \(\bar{K}^{0}\)-Meson umwandeln und umgekehrt.
Das führt beispielsweise dazu, dass in einem anfänglich reinen \(K^{0}\)-Mesonstrahl im Laufe der Zeit die Amplituden, ein \(K^{0}\) oder ein \(\bar{K}^{0}\)-Meson darin zu finden, periodisch oszillieren, analog zu den Neutrino-Oszillationen oben, wobei die Oszillation allerdings aufgrund des schnellen Zerfalls der \(K_{S}\)-Komponente rasch abnimmt und schließlich nur noch die \(K_{L}\)-Kombination übrig bleibt.
Die Zustände \(K^{0}\) und \(\bar{K}^{0}\) entsprechen dabei den Neutrino-Flavorzuständen, und \(K_{S}\) und \(K_{L}\) entsprechen den Neutrino-Massenzuständen (allerdings mit zusätzlicher unterschiedlicher Zerfallswahrscheinlichkeit neben der Masse).
Im Doppelpendel-Bild (siehe Neutrino-Oszillationen oben) entsprechen \(K^{0}\) und \(\bar{K}^{0}\) den beiden Pendeln, \(K_{L}\) entspricht der entgegengesetzten und \(K_{S}\) der parallelen Normalschwingung. Die Feder zwischen den Pendeln muss hier sehr schwach sein (geringer Massenunterschied) und die beiden Normalschwingungen müssten durch Reibung unterschiedlich gedämpft sein, wobei die parallele Normalschwingung sehr viel stärker gedämpft sein muss als die entgegengesetzte Normalschwingung, so dass nach kurzer Zeit nur noch diese Normalschwingung übrig bleibt und dann langsam abklingt.
Bei \(B^{0}\) und \(\bar{B}^{0}\)-Mesonen ( \( (d \bar{b}) \) bzw. \( (\bar{d} b) \), siehe unten) wäre die Feder dagegen stärker und die Dämpfung fast gleich, da die entsprechenden Massenzustände \(B_{H}\) (B-heavy) und \(B_{L}\) (B-light) einen Massenunterschied von immerhin \(3,3 \cdot 10^{-4}\) eV besitzen (bei etwa 5280 MeV Mesonmasse) sowie etwa gleiche Zerfallsraten.
Es gibt nun eine Symmetrie zwischen Materie und Antimaterie, die
im Rahmen relativistischer Quantenfeldtheorien streng erfüllt sein muss:
die CPT-Symmetrie. Man muss dabei nicht nur alle Teilchen durch Antiteilchen
ersetzen und alle Helizitäten (Spins) umdrehen, sondern auch den zeitgespiegelten Vorgang
(T = time reversal) betrachten, also Anfangs- und Endzustände vertauschen.
Die quantenmechanischen Amplituden für diesen CPT-gespiegelten Prozess
sollten dann dasselbe Längenquadrat besitzen wie der ursprüngliche Prozess.
Das hängt damit zusammen, dass man Antiteilchen als Teilchen interpretieren kann, deren Wellen sich formal rückwärts in der Zeit bewegen (Feynman-Stückelberg-Interpretation, siehe Zusatzinfos zu Kapitel 5.1). Bisher sprechen alle Messergebnisse für die Gültigkeit der CPT-Symmetrie. Das bedeutet, dass es aufgrund der CP-Verletzung auch eine T-Verletzung geben muss. Experimentell hat man sie in den Zerfällen neutraler K-Mesonen nachgewiesen. In diesem Sinn sind also die grundlegenden Gesetze der Natur nicht streng zeitsymmetrisch. Ob dies jedoch ausreicht, der Zeit immer eine Richtung zu geben und Zukunft sowie Vergangenheit klar zu unterscheiden, ist nicht ganz klar, da die T-Verletzung nur ein sehr kleiner Effekt ist. Insofern bietet immer noch die Entropie die einzige klare Möglichkeit, der Zeit eine Richtung zu geben (siehe Buchkapitel 7.2).
Im Rahmen des Standardmodells kann man die CP-Verletzung bei Quarks durch eine komplexe Phase in der CKM-Matrix der schwachen Wechselwirkung parametrisieren, die die Amplituden beschreibt, mit der die einzelnen Quarks über einen W-Boson-Vertex ineinander übergehen (Gravitation sowie starke und elektromagnetische Wechselwirkung sind dagegen C-, P- und damit CP-symmetrisch). Die CKM-Matrix entspricht genau der leptonischen Mischungsmatrix weiter oben, die zu Neutrinooszillationen führt – insofern kann es auch bei Neutrinos im Prinzip zur CP-Verletzung kommen. Gäbe es nur zwei Quarkfamilien, so könnte man die CKM-Matrix durch einen einzigen Drehwinkel (den Cabibbo-Winkel) parametrisieren, d.h. es gäbe keine komplexe Phase und somit keine CP-Verletzung. Im Standardmodell braucht man also für CP-Verletzung mindestens drei Quarkfamilien (und analog drei Leptonfamilien).
Die CP-Transformation (also der Übergang zu Antiteilchen mit anschließender Raumspiegelung) bewirkt mathematisch die komplexen Konjugation der W-Boson-Vertex-Amplituden inclusive der komplexen Phase der CKM-Matrix. Damit diese komplexe Phase zu einer CP-Verletzung in Zerfällen führen kann, müssen zwei Möglichkeiten zu einem Zerfallsprozess ungefähr gleichwertig beitragen, so dass die entsprechenden Wahrscheinlichkeitsamplituden (Pfeile) addiert werden müssen und ihre relative Phase zueinander dadurch wichtig wird (Interferenz).
Ein Beispiel dafür ist der Zerfall des neutralen \(\bar{B}^{0}\)-Mesons \( (\bar{d} b) \) in ein positives Pion \(\pi^{+} \; (\bar{d} u) \) und ein negatives Kaon \(K^{-} \; (\bar{u} s) \), also \[ \bar{B}^{0} \; \rightarrow \; \pi^{+} + K^{-} \] Die erste Möglichkeit für diesen Prozess besteht darin, dass das b-Quark sich unter Aussendung eines W-Bosons in ein u-Quark umwandelt und das W-Boson dann das komplette \(K^{-} \; (\bar{u} s) \) erzeugt.
Die zweite Möglichkeit besteht darin, dass das b-Quark zwar das W-Boson aussendet und sich in ein u-, c-, oder t-Quark umwandelt, aber dieses W-Boson wieder verschluckt und dabei in ein s-Quark übergeht, wobei es zuvor noch ein Gluon aussendet, das ein u- und ein \(\bar{u}\)-Quark erzeugt (man spricht hier von einem Pinguin-Diagramm). Tatsächlich findet man, dass die Zerfallsrate dieses Prozesses von derjenigen des CP-umgekehrten Prozesses \[ B^{0} \; \rightarrow \; \pi^{-} + K^{+} \] um etwa ein Prozent abweicht.
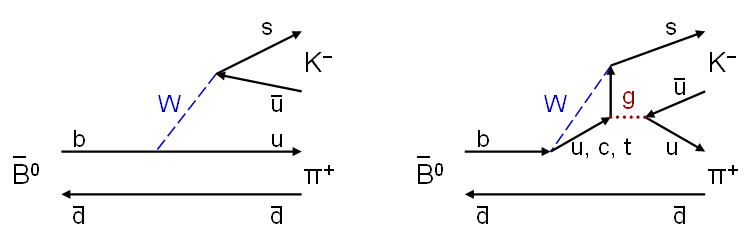
Zwei mögliche Feynmangraphen für den Zerfall
\( \bar{B}^{0} \; \rightarrow \; \pi^{+} + K^{-} \)
(hier wieder von links nach rechts zu lesen).
Bis zum Jahr 2010 konnte man alle bis dahin bekannten
CP-Verletzungen im Rahmen des Standardmodells erklären.
Dennoch vermutete man, dass es Abweichungen vom Standardmodell geben sollte.
So reicht die geringe CP-Verletzung des Standardmodells bei weitem nicht aus, um die
heute beobachtete Materiemenge im Universum erklären zu können,
denn dazu ist eine deutlich größere
CP-Verletzung notwendig. Außerdem liefert fast jede Erweiterung des Standardmodells zusätzliche
Quellen für CP-Verletzungen.
Im Mai 2010 gelang es der D0-Kollaboration (Tevatron, Fermilab) schließlich, erstmals eine CP-Verletzung zu finden, die deutlich größer ist als vom Standardmodell vorhergesagt (siehe Buchkapitel 6.1 und Buchkapitel 8.2). Dabei wurde der folgende seltene Prozess aus der Unmenge der möglichen Zerfallsprozesse herausselektiert:
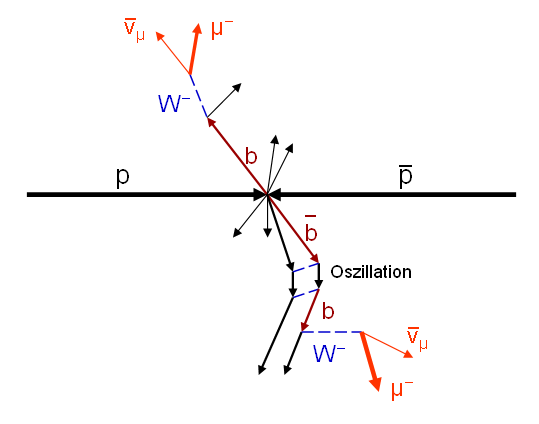
Es gibt dazu auch den CP-umgekehrten Prozess, bei dem das \(\bar{b}\)-Quark das erste Antimyon erzeugt und das b-Quark ein \(\bar{B}^{0}\)-Meson bildet, das in ein \(B^{0}\)-Meson übergeht und dann das zweite Antimyon erzeugt, so dass insgesamt zwei positiv geladene Antimyonen entstehen.
Beide Prozesse wurden aus der riesigen am Tevatron über mehrere Jahre erzeugten Datenmenge (etwa 6 fb-1 integrierte Luminosität) herausselektiert, von Untergrundprozessen befreit und miteinander verglichen. Dabei stellte man fest, dass Myonpaare um etwa 1 Prozent öfter auftreten als Anti-Myonpaare – eine klare Verletzung der CP-Symmetrie zwischen Materie und Antimaterie, zumal der Anfangszustand aus Proton und Antiproton vollkommen CP-symmetrisch ist.
Das Standardmodell sagt dagegen nur einen Überschuss von etwa 0,02 Prozent voraus – ein deutlicher Hinweis auf Physik jenseits des Standardmodells (siehe auch die Zusatzinfos zu Kapitel 8.2). Zu weiteren Details siehe die Original-Veröffentlichung: The D0 Collaboration: Evidence for an anomalous like-sign dimuon charge asymmetry, http://arxiv.org/abs/1005.2757
Die CP-Verletzung bietet also ein vielversprechendes Fenster in die Physik jenseits des Standardmodells. Es wird spannend sein, was die verschiedenen Experimente dazu noch alles herausfinden werden, insbesondere am LHCb-Detektor am LHC (CERN), aber auch aan den sogenannten B-Meson-Fabriken (z.B. das BaBar-Experiment am SLAC, Stanford, USA oder das Belle-Experiment am KEK, Tsukuba, Japan) sowie in den vielen Experimenten zu Neutrino-Oszillationen (siehe oben).
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 11 January 2024