
Sir Isaac Newton (1642 - 1727), gemalt von Godfrey Kneller im Jahr 1689.
Quelle: Wikimedia Commons File:GodfreyKneller-IsaacNewton-1689.jpg, dort public domain.
Zusammenfassung des Buchkapitels:
Wenn wir Materie verstehen wollen, so müssen wir uns sowohl mit den elementaren Teilchen als auch auch mit den Wechselwirkungen zwischen ihnen befassen. Newton formulierte dazu seine zwei berühmten Bewegungsgesetze (eigentlich waren es historisch drei Bewegungsgesetze – mehr dazu siehe unten in den Zusatzinfos):

Sir Isaac Newton (1642 - 1727),
gemalt von Godfrey Kneller im Jahr 1689.
Quelle:
Wikimedia Commons File:GodfreyKneller-IsaacNewton-1689.jpg, dort public domain.
Man kennt heute vier grundlegende Wechselwirkungen (Kräfte) zwischen den Bausteinen der Materie:
Gravitation (Schwerkraft):
Die anziehende Schwerkraft \(F\) zwischen zwei kleinen Körpern der Masse \(m_{1}\) und \(m_{2}\) im Abstand \(r\) voneinander wird recht genau durch Newtons Gravitationsgesetz beschrieben: \[ F = G \, \frac{m_{1} \, m_{2}}{r^{2}} \] Die Gravitationskonstante \[ G = 6,674 \cdot 10^{-11} \, \frac{\mathrm{m}^{3}}{\mathrm{kg} \cdot \mathrm{s}^{2}} \] braucht man, da man schwere und träge Masse gleichsetzt (mehr dazu im Buch).
elektromagnetische Wechselwirkung:
Sie beschreibt die elektrischen und magnetischen Kräfte zwischen elektrischen Ladungen. Das Kraftgesetz zwischen zwei ruhenden elektrischen Ladungen \(q_{1}\) und \(q_{2}\) sieht vollkommen analog zu Newtons Gravitationsgesetz aus: \[ F = k \, \frac{q_{1} \, q_{2}}{r^{2}} \] mit dem Proportionalitätsfaktor \[ k = 9 \cdot 10^{9} \, \frac{\mathrm{N} \cdot \mathrm{m}^{2}}{\mathrm{C}^{2}} \] den man im SI-Einheitensystem aufgrund der Ladungsdefinition über die Stromstärke braucht (Details im Buch). Oft schreibt man auch \[ k = \frac{1}{4 \pi \epsilon_{0}} \] mit der elektrischen Feldkonstanten \[ \epsilon_{0} = 0,854 \cdot 10^{-11} \, \frac{\mathrm{C}^{2}}{\mathrm{N} \, \mathrm{m}^{2}} \] (das große C steht für die SI-Ladungseinheit Coulomb) mit der Lichtgeschwindigkeit \[ c = 299 \,792 \,458 \, \frac{\mathrm{m}}{\mathrm{s}} \] Es gilt die exakte Definition: \[ k = 10^{-7} \, c^2 \, \frac{\mathrm{N} \cdot \mathrm{m}^{2}}{\mathrm{C}^{2}} \, \left( \frac{\mathrm{s}}{\mathrm{m}} \right)^2 \] Mehr dazu in den Zusatzinfos unten.
Im Unterschied zur Gravitation, die immer anziehend zwischen zwei Körpern wirkt, gibt es sowohl anziehende als auch abstoßende elektrische Kräfte und entsprechend positive und negative elektrische Ladungen. Die elektrische Kraft zwischen geladenen Teilchen ist dabei sehr viel stärker als die Schwerkraft zwischen ihnen.
Bei bewegten elektrischen Ladungen kommen Magnetfelder hinzu. Die genauen Zusammenhänge werden durch die Maxwellgleichungen beschrieben. Letztlich haben Magnetfelder ihre Ursache in der speziellen Relativitätstheorie Einsteins, aus der sich auch die obige Formel zwischen \(k\) und der Lichtgeschwindigkeit \(c\) ergibt (siehe Zusatzinfos unten). Der Zusammenhang zwischen elektrischen und magnetischen Kräften führt also auf eine universelle Naturkonstante: die Lichtgeschwindigkeit \(c\).

Quelle:
Wikimedia Commons File:James Clerk Maxwell big.jpg, dort gemeinfrei
In Kurzform lauten die Maxwellgleichungen (zur Veranschaulichung siehe unten die Zusatzinfos):
Elektrische und magnetische Felder lassen sich überlagern, ohne sich zu stören (Superpositionsprinzip):
Erst bei der Betrachtung der
Atomkerne und ihrer Zerfälle werden wir später auf die
schwache und die starke Wechselwirkung stoßen.
As for the forces, electromagnetism and gravity we experience in everyday life. But the weak and strong forces are beyond our ordinary experience. So in physics, lots of the basic building blocks take 20th- or perhaps 21st-century equipment to explore.
Zitat von Edward Witten, siehe Internet
From a long view of the history of mankind – seen from, say, ten thousand years from now – there can be little doubt that the most significant event of the 19th century will be judged as Maxwell's discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade.
Richard Feynman in The Feynman Lectures on Physics, Volume II, 1-6 end
a) Newtons Grundgesetze der Mechanik
b) Der Zusammenhang zwischen k und c
c) Die Maxwellgleichungen
d) Der relativistische Ursprung des Magnetfeldes
e) relativistische Formulierung der Maxwellgleichungen
Historisch hat Newton nicht zwei, sondern drei Bewegungsgesetze formuliert, siehe z.B. Wikipedia: Newtonsche Gesetze. Das erste Bewegungsgesetz (das Trägheitsprinzip) ist jedoch ein Spezialfall seines zweiten Bewegungsgesetzes (Kraft = Masse × Beschleunigung), so dass ich es im Buchtext der ersten Auflage nicht separat aufgeführt habe (in der zweiten Auflage dagegen schon).
Wie kommt man auf Newtons Bewegungsgesetze, und was bedeuten sie physikalisch? Mehr dazu finden Sie in Die Symmetrie der Naturgesetze, Kapitel 2.1: Einige Gedanken zu den Begriffen Bahnkurve, Kraft und Masse. Auch einiges zum Impuls-Begriff steht dort und im Folgekapitel 2.2.
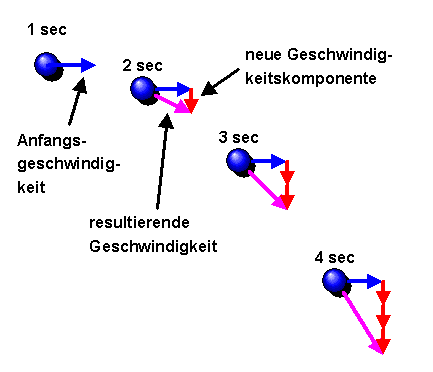
Häufig formuliert man das Bewegungsgesetz \[ \boldsymbol{F} = m \; \boldsymbol{a} \] auch in der allgemeineren Form \[ \boldsymbol{F} = \frac{d\boldsymbol{p}}{dt} \] d.h. die Kraft \(\boldsymbol{F}\) ist gleich der zeitlichen Änderung des Impulses \(\boldsymbol{p}\) des Objektes, auf das die Kraft wirkt. Anschaulich ist der Impuls daher ein gespeicherter Kraftstoß, also gleichsam der Schwung eines Objektes. Ohne eine wirkende Kraft ist der Impuls zeitlich konstant.
Bei kleinen Geschwindigkeiten (relativ zur Lichtgeschwindigkeit \(c\)) ist der Impuls eines Objektes der Masse \(m\) und Geschwindigkeit \(\boldsymbol{v}\) gegeben durch \[ \boldsymbol{p} = m \, \boldsymbol{v} \] was dann von \( \boldsymbol{F} = \frac{d\boldsymbol{p}}{dt} \) zu \[ \boldsymbol{F} = m \, \boldsymbol{a} \] führt.
Die allgemeine Formel \[ \boldsymbol{F} = \frac{d\boldsymbol{p}}{dt} \] ist aber auch für schnelle Teilchen korrekt, wobei dann der relativistische Teilchenimpuls \[ \boldsymbol{p} = m \gamma \boldsymbol{v} \] verwendet werden muss mit \[ \gamma = \frac{1}{\sqrt{1 - (v/c)^{2}}} \] (mehr dazu siehe Kapitel 3.2).
Eine physikalische Bedeutung erhält dieses Bewegungsgesetz erst, wenn man noch irgendeine Zusatzinformation über die Kraft hat, aus der man diese berechnen kann, beispielsweise über Newtons Gravitationsgesetz.
Wenn man \( \boldsymbol{F} = m \, \boldsymbol{a} \) nur als Definition der Kraft versteht, gewinnt man nicht viel, denn dann hat man nur einen neuen Begriff für das Produkt aus Masse mal Beschleunigung eingeführt. Man muss weitere Informationen unabhängig von diesem Gesetz über die wirkende Kraft besitzen, und diese Informationen müssen in gewissem Sinn einfach sein. Ein Beispiel für diese Einfachheit wäre die Beobachtung, dass Kräfte einen materiellen Ursprung haben. Wenn weit und breit kein anderer Körper vorhanden ist, so sollte auch keine Kraft wirken.
Richard Feynman hat in seinen Feynman Vorlesungen über Physik, Band 1: Mechanik, Strahlung, Wärme (Kapitel 12-1) zur Verdeutlichung dieses Gedankens scherzhaft den Begriff Schmaft (englisch: gorce) eingeführt:
Auch das ist eine Definition, ähnlich der Definition der Kraft (ein Objekt beschleunigt nur, wenn eine Kraft auf es einwirkt – ansonsten bewegt es sich mit konstanter Geschwindigkeit). Aber anders als die Kraft wäre diese Schmaft nicht einfach. So beobachten wir im leeren Weltall fernab von anderen Objekten, dass eine antriebslose Raumkapsel sich geradlinig-gleichförmig bewegt, ohne zum Stillstand zu kommen.
Natürlich könnten wir sagen, dass dann eine Schmaft auf das Raumschiff wirken muss, aber diese Aussage wäre vollkommen bedeutungslos und würde uns bei der Beschreibung der Welt nicht weiterhelfen. Das ist vollkommen anders, wenn wir \( \boldsymbol{F} = m \, \boldsymbol{a} \) haben und beispielsweise die Gravitationskraft über Newtons Gravitationsgesetz berechnen – schon können wir die Planetenbahnen im Schwerefeld der Sonne berechnen und uns ansehen, ob sich die Planeten tatsächlich so bewegen. Und im leeren Weltall fernab von anderen Objekten wirkt dann eben keine relevante Kraft, so dass sich die Raumkapsel auch geradlinig-gleichförmig bewegt. Eine Schmaft brauchen wir dann nicht mehr, um das zu erklären.
Actio gleich Reactio:
Das Gesetz Actio gleich Reactio besagt, dass in einem abgeschlossenen System aus mehreren Objekten, auf das keine äußere Kraft wirkt, die Summe aller inneren Kräfte gleich Null ist. Die inneren Kräfte können also zwar zu inneren Impulsflüssen zwischen den Objekten führen, nicht aber den Gesamtimpuls des Systems ändern. Das ist der Impulserhaltungssatz. Übrigens ist es manchmal nützlich, sich auch bei einem statischen System die insgesamt ausgeglichenen inneren Kräfte (Spannungen) als Impulsflüsse vorzustellen, die sich gegenseitig neutralisieren. Diese Impulsflüsse werden spätestens dann wichtig, wenn man zur Relativitätstheorie übergeht.
Wenn man ganz genau hinschaut, so scheint das Gesetz Actio gleich Reactio und damit die Impulserhaltung manchmal für kurze Zeiten verletzt zu sein, denn nach der speziellen Relativitätstheorie dauert es immer eine kurze Zeit, bis ein Objekt auf ein anderes Objekt eine Kraft ausüben kann (denn nichts kann sich schneller als das Licht bewegen, auch keine Kraftwirkung). Der zwischen den Objekten übertragene Impuls scheint für kurze Zeit verborgen zu sein. Im Fall elektromagnetischer Kräfte steckt dieser Impuls im elektromagnetischen Feld, das die Kräfte überträgt, d.h. auch elektromagnetische Felder haben Impuls (und Energie). Sobald wir später elektromagnetische Felder durch Photonen beschreiben, werden wir sagen können: auch Photonen besitzen Impuls! Sobald wir diese Impulse mit berücksichtigen, ist mit der Impulserhaltung wieder alles in Ordnung.
Der oben und im Buchkapitel dargestellte Zusammenhang zwischen der Proportionalitätskonstante k und der Lichtgeschwindigkeit c ergibt sich so:
Die Stromeinheit Ampere ist im SI-Einheitensystem über die Anziehungskraft zwischen zwei parallelen stromführenden Drähten definiert (siehe Wikipedia: Ampere sowie weiter unten unter dem Punkt Ampèresches Gesetz). Diese Anziehungskraft entsteht durch das Magnetfeld, das durch die Ströme erzeugt wird. Die Definition des Amperes kann man daher in eine Definition der magnetischen Feldkonstanten \(\mu_{0}\) übersetzen, d.h. es gilt exakt \[ \mu_{0} = 4\pi \cdot 10^{- 7} \frac{N}{A^{2}} \] (seit 1919 ist allerdings das SI-System geändert worden, sodass \(\mu_{0}\) seitdem zu einer Messgröße geworden ist, die Messunsicherheiten aufweist).
Aus den Maxwellgleichungen lässt sich nun eine Wellengleichung für elektromagnetische Wellen herleiten. Das geht so:
Nach dem Faradayschen Induktionsgesetz (siehe unten) erzeugt ein sich veränderndes Magnetfeld ein elektrisches Wirbelfeld: \[ \mathrm{rot} \, \boldsymbol{E} = - \frac{d\boldsymbol{B}}{dt} \] Nach dem Ampèreschen Gesetz (siehe unten) erzeugt im stromfreien Raum umgekehrt ein sich veränderndes elektrisches Feld ein magnetisches Wirbelfeld: \[ \mathrm{rot} \, \boldsymbol{B} = \mu_{0} \epsilon_{0} \, \frac{d\boldsymbol{E}}{dt} \] Wendet man auf die erste Gleichung erneut den Rotationsoperator an, so ergibt sich mithilfe der zweiten Gleichung \[ \mathrm{rot} \, (\mathrm{rot} \, \boldsymbol{E}) = \] \[ = - \frac{d}{dt} \, (\mathrm{rot} \, \boldsymbol{B}) = \] \[ = - \frac{d}{dt} \left( \mu_{0} \epsilon_{0} \frac{d\boldsymbol{E}}{dt} \right) = \] \[ = - \mu_{0} \epsilon_{0} \, \frac{d^2}{dt^2}\boldsymbol{E} \] Zugleich ist \[ \mathrm{rot} \, (\mathrm{rot} \, \boldsymbol{E}) = \] \[ = \mathrm{grad} \, (\mathrm{div} \, \boldsymbol{E}) - \frac{d^2}{d\boldsymbol{x}^2} \boldsymbol{E} \] und im ladungsfreien Raum gilt zusätzlich \( \mathrm{div} \, \boldsymbol{E} = 0 \), so dass nur der zweite Term stehen bleibt. Damit erhalten wir die Wellengleichung \[ \frac{d^2}{d\boldsymbol{x}^2} \boldsymbol{E} = \mu_{0} \epsilon_{0} \, \frac{d^2}{dt^2} \boldsymbol{E} \] Eine analoge Gleichung lässt sich für \(\boldsymbol{B}\) herleiten. Man kann sich nun überlegen, dass Wellen (z.B. Sinuswellen) mit einer Geschwindigkeit von \[ c = \frac{1}{\sqrt{\epsilon_{0} \mu_{0}}} \] diese Gleichung lösen. Wir wollen das am Beispiel einer in x-Richtung laufenden ebenen Sinuswelle überprüfen, für die wir den Ansatz \[ \boldsymbol{E} = \boldsymbol{E}_{0} \, \sin{ \left( \frac{2 \pi}{\lambda} \, x - 2 \pi f \, t \right) } \] machen, wobei wir das Argument des Sinus (die Phase \(\phi\)) im Bogenmaß angeben – daher der Faktor \(2\pi\).
Anschaulich ist damit \(\lambda\) die räumliche Wellenlänge und \(f\) die zeitliche Frequenz. Eine konstante Wellenhöhe (z.B. ein Wellenberg) entspricht nun einem konstanten Wert für die Phase \[ \phi = \frac{2 \pi}{\lambda} \, x - 2 \pi f \, t \] und die Stellen konstanter Phase \( \phi \) wandern mit der Zeit \(t\) nach der obigen Formel entlang der x-Achse. Aufgelöst nach \(x\) ergibt das die Gleichung \[ x = \lambda f t + \frac{\lambda}{2 \pi} \, \phi \] d.h. die Welle bewegt sich mit der Geschwindigkeit \[ c = \lambda f \] Wenn wir nun den obigen Ansatz in die Wellengleichung einsetzen, so ergibt das \[ \left( \frac{2 \pi}{\lambda} \right)^{2} = \mu_{0} \epsilon_{0} \, (2 \pi f)^{2} \] und somit \[ (\lambda f)^{2} = \frac{1}{\mu_{0} \epsilon_{0}} \] Da \( \lambda f \) gleich der Wellengeschwindigkeit \(c\) ist, haben wir damit unser Ergebnis \[ c^{2} = \frac{1}{\epsilon_{0} \mu_{0}} \] abgeleitet.
Alle elektromagnetischen Wellen (also auch Licht) haben nach der obigen Wellengleichung dieselbe Geschwindigkeit \(c\), die mit der elektrischen und magnetischen Feldkonstanten so zusammenhängt (siehe auch Wikipedia: Elektrische Feldkonstante):
| \[ c^{2} = \frac{1}{\epsilon_{0} \mu_{0}} \] |
Daraus ergibt sich für \(k\) der exakte Wert (sofern man \(\mu_{0}\) exakt vorgibt)
\[
k = \frac{1}{4 \pi \epsilon_{0}} =
\frac{\mu_{0} c^{2}}{4 \pi} =
\]
\[
= 10^{- 7} \, c^2 \, \frac{\mathrm{N}}{\mathrm{A}^{2}} =
\]
\[
= 10^{- 7} \, c^2 \, \frac{\mathrm{N} \, \mathrm{s}^{2}}{\mathrm{C}^{2}} =
\]
\[
= 10^{- 7} \, c^2 \, \frac{\mathrm{N} \, \mathrm{m}^{2}}{\mathrm{C}^{2}} \, \frac{\mathrm{s}^{2}}{\mathrm{m}^{2}}
\]
Zwei Ladungen von je einem Coulomb im Abstand von einem Meter üben also aufeinander
die Kraft von \( 10^{- 7} \cdot (299 \, 792 \, 458)^{2} \) Newton aus.
Das sind ziemlich genau 9 Milliarden Newton, also die Gewichtskraft von knapp 1 Millionen Tonnen.
Setzt man in guter Näherung die Lichtgeschwindigkeit gleich \( 3 \cdot 10^{8}\) m/s ,
so ergibt sich der oben genannte Wert von
\[
k = 9 \cdot 10^{9} \, \frac{\mathrm{N} \, \mathrm{m}^{2}}{\mathrm{C}^{2}}
\]
Die genaue mathematische Form der Maxwellgleichungen finden Sie auch am Anfang von Quantenfeldtheorie und Eichfelder, Kapitel 4: Die kanonische Quantisierung des freien elektromagnetischen Feldes,, wobei dort allerdings keine SI-Einheiten verwendet werden. Wir verwenden im folgenden analog zum Buch SI-Einheiten (mehr zu anderen Einheitensystemen siehe weiter unten):
Definition des elektrischen und des magnetischen Feldes:
Elektrisches und magnetisches Feld werden definiert, um den Begriff der Fernwirkung von räumlich entfernten Ladungen aufeinander zu umgehen und durch eine lokale Beschreibung zu ersetzen. Man beschreibt also nicht direkt die Kräfte, die Ladungen aufeinander ausüben, sondern Ladungen erzeugen zunächst elektromagnetische Felder im umgebenden Raum, und die lokale Stärke dieser Felder an einem Ort \(\boldsymbol{x}\) bestimmt anschließend, welche Kraft auf eine an diesem Ort befindliche Ladung wirkt. Damit lässt sich die endliche Ausbreitungsgeschwindigkeit elektromagnetischer Kräfte viel leichter beschreiben als ohne den Feldbegriff.
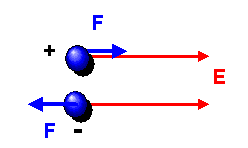
Ein elektrisches Feld \(\boldsymbol{E}\) erzeugt bei einer Ladung \(Q\) die Kraft \[ \boldsymbol{F} = Q \, \boldsymbol{E} \] Dabei kann \(Q\) positiv oder negativ sein:
Ein Magnetfeld \(\boldsymbol{B}\) erzeugt bei einer bewegten Ladung \(Q\) die Lorentzkraft
\[
\boldsymbol{F} = Q \, \boldsymbol{v} \times \boldsymbol{B}
\]
(wobei \(\times\) für das Kreuzprodukt von Vektoren steht,
siehe Wikipedia: Kreuzprodukt).
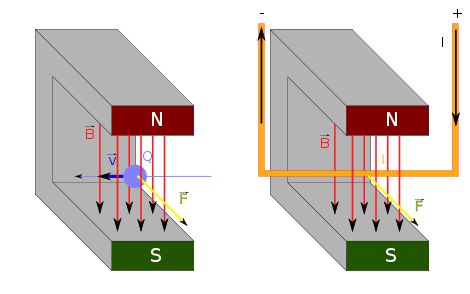
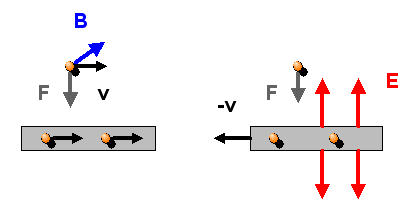
Die Kraft \(\boldsymbol{F}\) steht dabei senkrecht zur Geschwindigkeit \(\boldsymbol{v}\) und dem Magnetfeld \(\boldsymbol{B}\) (siehe unten das Bild links).
Bei stromführenden dünnen Leiter mit Stromstärke \(I\) ist \[ Q \, \boldsymbol{v} = I \, dt \, \frac{\boldsymbol{ds}}{dt} = I \, \boldsymbol{ds} \] Dabei ist \(Q\) die kleine Ladungsmenge, die der Strom während der Zeit \(dt\) durch ein kleines Leiterstück der Länge \( \boldsymbol{ds} \) transportiert. Auf das kleine Leiterstück wirkt also die Kraft \[ d\boldsymbol{F} = I \, \boldsymbol{ds} \times \boldsymbol{B} \] (siehe das rechte Bild unten). Nach diesem Prinzip funktionieren beispielsweise Elektromotoren.
Quelle:
Wikimedia Commons File:Lorentzkraft v2.svg,
Credit: Honina, Ladyt,
CC BY-SA 3.0 DEED
Zusammengefasst gilt:
| \[ \boldsymbol{F} = Q \, (\boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B}) \] |
Coulombsches Kraftgesetz:
Bei einer elektrischen Punktladung zeigt das elektrische Feld radial nach außen und nimmt bei wachsendem Abstand \(r\) zur Ladung mit \(1/r^{2}\) ab:
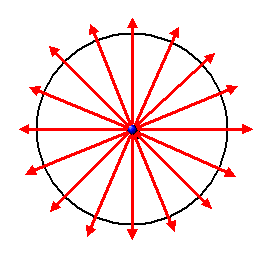
Man kann auch anschaulich sagen: Die elektrische Feldstärke entspricht der Dichte
der roten Feldlinien, die ebenfalls mit \(1/r^{2}\) abnimmt.
Legt man um die Ladung herum eine geschlossene Oberfläche (im Bild oben durch den schwarzen Kreis dargestellt),
so ist die Anzahl der elektrischen Feldlinien,
die die Fläche nach außen durchstoßen
(der sogenannte elektrische Fluss durch die Fläche) proportional zur darin
eingeschlossenen Ladung. Ladungen sind gleichsam Quellen für den elektrischen Fluss.
Die genaue Formel dafür lautet
| \[ \epsilon_{0} \, \int_{\delta V} \boldsymbol{E \, dA} = q \] |
mit der elektrischen Feldkonstanten \(\epsilon_{0}\), wobei \(q\) die im Volumen \(V\) enthaltene elektrische Ladungsmenge und \(\delta V\) der Rand (die Oberfläche) dieses Volumens ist, d.h. das Integral ergibt den elektrischen Fluss durch diese Oberfläche.
Diese Gleichung gilt auch für kompliziertere elektrische Felder und bewegte Ladungen, deren Feld nicht gleichförmig radial ist. In differentieller Form lautet diese Gleichung
| \[ \mathrm{div} \, \boldsymbol{E} = \frac{\rho}{\epsilon_{0}} \] |
mit der Ladungsdichte \(\rho\) (Ladung pro Volumen).
Bei einer ruhenden punktförmigen Ladung \(q\) im Mittelpunkt eines Kugelvolumens \(V\) mit Radius \(r\) ist \[ q = \epsilon_{0} \, \int_{\delta V} \boldsymbol{E \, dA} = \epsilon_{0} \, E \, 4\pi r^{2} \] mit \(E = |\boldsymbol{E}|\) und somit \[ E = \frac{1}{4 \pi \epsilon_{0}} \, \frac{q}{r^{2}} \] Die Kraft auf eine Probeladung \(Q\) im Abstand \(r\) von der Ladung \(q\) ist also gleich \[ F = Q \, E = \frac{1}{4 \pi \epsilon_{0}} \, \frac{Q \, q}{r^{2}} \] Das ist genau das bekannte Coulombsche Kraftgesetz zwischen zwei ruhenden elektrischen Ladungen.
Gauß'sches Gesetz des Magnetismus:
Magnetfelder haben keine Quellen, sondern bestehen aus Wirbeln (geschlossenen Feldlinien). Es gibt also keine magnetischen Ladungen, an denen magnetische Feldlinien starten oder enden:
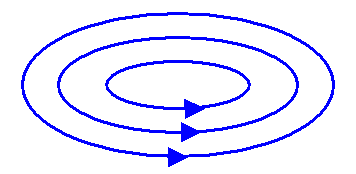
Magnetfelder haben keine Quellen, sondern bilden immer geschlossene Feldlinien (Wirbel)
Legt man eine geschlossene Oberfläche (z.B. eine Kugeloberfläche)
in ein Magnetfeld, so treten genauso viele
Magnetfeldlinien in das dadurch eingeschlossene Volumen hinein wie heraus, d.h. der magnetische
Fluss durch eine geschlossenen Oberfläche ist Null.
In Analogie zum elektrischen Fluss oben lautet die Formel dafür
| \[ \int_{\delta V} \boldsymbol{B \, dA} = 0 \] |
wobei wieder \( \delta V \) der Rand (die Oberfläche) des Volumens \(V\) ist, d.h. das Integral ergibt den magnetischen Fluss durch diese Oberfläche. In differentieller Form lautet diese Gleichung
| \[ \mathrm{div} \, \boldsymbol{B} = 0 \] |
Faradaysches Induktionsgesetz:
Ein sich veränderndes Magnetfeld erzeugt ein elektrisches Wirbelfeld. In einer geschlossene Leiterschleife entsteht aufgrund des elektrischen Wirbelfeldes eine elektrische Spannung, die proportional zur zeitlichen magnetischen Flussänderung durch die Leiterschleife ist. Dabei ist der magnetische Fluss anschaulich die Zahl der Magnetfeldlinien, die die Fläche durchstoßen, deren Rand die Leiterschleife bildet. Je mehr dieser Fluss zeitlich zu- oder abnimmt, umso stärker ist die induzierte elektrische Spannung. Nach diesem Prinzip funktionieren Dynamos und andere elektrische Generatoren.
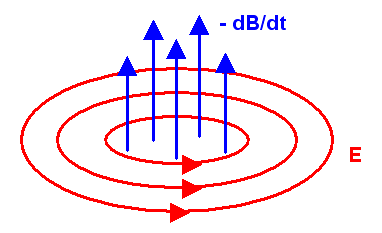
In Formeln ausgedrückt ist der magnetische Fluss durch die Fläche \(A\), deren Rand \(\delta A\)
die Leiterschleife bildet, gleich
\[
\int_{A} \boldsymbol{B \, dA}
\]
Die induzierte Spannung in der Leiterschleife ist wiederum gleich
\[
\int_{\delta A} \boldsymbol{E \, ds}
\]
und es gilt:
| \[ \int_{\delta A} \boldsymbol{E \, ds} = - \frac{d}{dt} \, \int_{A} \boldsymbol{B \, dA} \] |
In differentieller Form lautet diese Gleichung
| \[ \mathrm{rot} \, \boldsymbol{E} = - \frac{d\boldsymbol{B}}{dt} \] |
Ampèresches Gesetz:
Ein elektrischer Strom sowie ein sich veränderndes elektrisches Feld erzeugen ein magnetisches Wirbelfeld:
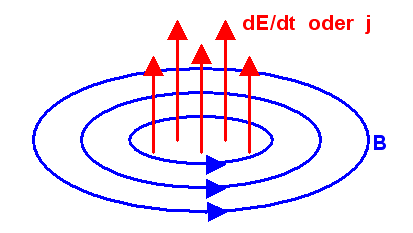
Legt man eine geschlossene Schleife \( \delta A \) in dieses Feld,
so kann man das Magnetfeld entlang dieser Schleife aufintegrieren (man könnte formal von einer
magnetischen Spannung sprechen).
Dieses Magnetfeld-Schleifenintegral
\[
\int_{\delta A} \boldsymbol{B \, ds}
\]
hängt mit dem Stromfluss
\[
I = \int_{A} \boldsymbol{j \, dA}
\]
und dem elektrischen Feldfluss
\[
\int_{A} \boldsymbol{E \, dA}
\]
durch die Schleifenfläche \(A\) zusammen
(dabei ist \(\boldsymbol{j}\) die Flächenstromdichte):
Je größer der Stromfluss ist oder je mehr der elektrische Fluss sich
zeitlich ändert, umso stärker ist
das Magnetfeld-Schleifenintegral:
| \[ \int_{\delta A} \boldsymbol{B \, ds} = \mu_{0} \, I + \mu_{0} \epsilon_{0} \, \frac{d}{dt} \, \int_{A} \boldsymbol{E \, dA} \] |
mit der magnetischen Feldkonstanten \(\mu_{0}\) und der elektrischen Feldkonstanten \(\epsilon_{0}\). In differentieller Form lautet diese Gleichung
| \[ \mathrm{rot} \, \boldsymbol{B} = \mu_{0} \, \boldsymbol{j} + \mu_{0} \epsilon_{0} \, \frac{d\boldsymbol{E}}{dt} \] |
Nach diesem Prinzip funktionieren beispielsweise Elektromagneten.
Die Einbeziehung des elektrischen Flusses bei der Magnetfelderzeugung ist ein wichtiger Punkt, den man schnell übersehen kann. Nur so erhält man ein konsistentes Bild, wenn man beispielsweise in ein stromführendes Kabel einen Kondensator einbaut – zwischen den beiden Kondensatorplatten fließt kein Strom, aber beim Aufladen verstärkt sich das elektrische Feld zwischen den Platten, so dass sowohl das Kabel als auch der Kondensator von einem ringförmigen Magnetfeld umschlunden werden.
Etwas abstrakter kann man sagen: Nur wenn man die Änderung des elektrischen Flusses bei der Erzeugung von Magnetfeldern mit einbezieht, gerät man nicht in Konflikt mit dem Erhaltungssatz für die elektrische Ladung – mehr dazu weiter unten (Kontinuitätsgleichung).
Man kann nun leicht die magnetische Anziehungskraft zwischen zwei parallelen Leitern im Abstand \(r\) voneinander angeben, durch die parallel je ein elektrischer Strom \(I\) fließt:
Dazu legen wir um einen der Leiter im Radius \(r\) eine Kreißchleife, so dass gilt: \[ \int_{\delta A} \boldsymbol{B \, ds} = B \, 2 \pi r = \mu_{0} \, I \] (mit \(B = |\boldsymbol{B}|\)) und somit \[ B = \mu_{0} \, \frac{I}{2 \pi r} \] wobei das Magnetfeld den Leiter ringförmig umläuft.
Auf den anderen Leiter wird pro Leiterstück \( \boldsymbol{ds} \) durch das Magnetfeld die Kraft \[ d\boldsymbol{F} = I \, \boldsymbol{ds} \times \boldsymbol{B} \] ausgeübt (siehe oben). Da Magnetfeld und Leiterstück senkrecht aufeinander stehen, gilt für die Beträge: \[ dF = I \, ds \, B = I \, ds \, \mu_{0} \, \frac{I}{2 \pi r} \] Im SI-Einheitensystem legte man früher die Stromstärke-Einheit Ampere (A) gerade so fest, dass \( \mu_{0} \) den festen Wert \[ \mu_{0} = 4\pi \cdot 10^{- 7} \frac{\mathrm{N}}{\mathrm{A}^{2}} \] erhält. Das Ampere war also gerade so definiert, dass zwei parallele stromführende Leiter mit je \( I = 1 \) Ampere Strom im Abstand \( r = 1\) Meter pro Leiterlänge \( ds = 1 \) Meter aufeinander eine Kraft von \[ dF = I \, ds \, \mu_{0} \, \frac{I}{2 \pi r} = \] \[ = 1 \mathrm{A} \cdot 1 \mathrm{m} \, \left( 4 \pi \cdot 10^{- 7} \frac{\mathrm{N}}{\mathrm{A}^{2}} \right) \, \frac{ 1 \mathrm{A} }{2 \pi \cdot 1 \mathrm{m}} = \] \[ = 2 \cdot 10^{- 7} \mathrm{N} \] ausüben. Das ist genau die auch im Buchkapitel angegebene (ehemalige) Definition der Stromstärke-Einheit Ampere.
Eine super-animierte Grafik des elektromagnetischen Feldes,
das eine Dipol-Antenne abstrahlt, findet man übrigens unter
Wikimedia Commons File:DipoleRadiation.gif.
So sieht es aus, wenn man den Maxwellgleichungen Leben einhaucht!
Sich ändernde elektrische und magnetische Felder können sich von ihrer Quelle ablösen und sich
aufgrund der Maxwellgleichungen oben gegenseitig am Leben erhalten. Das ist das Geheimnis der
elektromagnetischen Wellen.
zu den Maßeinheiten:
Bisher haben wir die Maxwellgleichungen im SI-Einheitensystem angegeben, bei der (früher) zunächst die magnetische Feldkonstante \(\mu_{0}\) festgelegt und damit die Stromeinheit Ampere über die magnetischen Kräfte definiert wird. Über die Stromeinheit ist dann automatisch eine Ladungseinheit definiert (nämlich die pro Zeit transportierte Ladung), in diesem Fall das Coulomb: 1 Coulomb = 1 Ampere × 1 Sekunde.
Die elektrische Feldkonstante \( \epsilon_{0} \) ist dann über die elektromagnetischen Wellen festgelegt, also \( c^{2} = 1 / (\epsilon_{0} \mu_{0}) \). Zusammengefasst beginnt man hier mit den magnetischen Kräften und der Stromeinheit, wodurch die elektrischen Kräfte und die Ladungseinheit festgelegt sind.
Man hätte übrigens auch auf die Stromeinheit Ampere verzichten können und der magnetischen Feldkonstanten \( \mu_{0} \) beispielsweise den Wert Eins zuordnen können. Die Stromeinheit wäre dann gemäß der Formel (siehe oben) \( dF = I^{2} \, ds / (2 \pi r) \) einfach gleich \( \sqrt{\mathrm{N}} \), die Ladungseinheit wäre gleich \( \mathrm{s} \cdot \sqrt{\mathrm{N}} \) und die elektrische Feldkonstante wäre \( \epsilon_{0} = 1/c^{2} \).
Eine andere Möglichkeit besteht darin, mit den elektrischen Kräften zu beginnen. So könnte man der elektrischen Feldkonstanten \( \epsilon_{0} \) den Wert Eins zuordnen und so die Ladungseinheit festlegen. Die Ladung würden dann in der Einheit \( \mathrm{m} \cdot \sqrt{\mathrm{N}} \) gemessen, die Stromstärke in der Einheit \( \mathrm{m} \cdot \sqrt{\mathrm{N}} / \mathrm{s} \) und die magnetische Feldkonstante wäre \( \mu_{0} = 1/c^{2} \). Diese Maßeinheiten haben wir in Quantenfeldtheorie und Eichfelder, Kapitel 4 verwendet, wobei dort das Magnetfeld noch einen Faktor \(c\) enthält (Heaviside-Maßeinheiten).
Die Kontinuitätsgleichung:
Elektrische Ladung kann weder erzeugt noch vernichtet werden. Für sie gilt daher die folgende Kontinuitätsgleichung:
| \[ \frac{d}{dt} \, \int_{V} \, \rho \, dV = - \int_{\delta V} \, \boldsymbol{j \, dA} \] |
Dabei ist \(V\) ein Raumvolumen, \(\delta V\) ist die Oberfläche des Volumens, \(\rho\) ist die Ladungsdichte und \(\boldsymbol{j}\) die Flächenstromdichte. Das Volumenintegral links ist also die im Volumen \(V\) enthaltene Gesamtladung, und das Flächenintegral rechts ist der elektrische Strom, der das Volumen \(V\) über seine Oberfläche verlässt. Die Gleichung sagt also, dass ein elektrischer Strom, der das Volumen \(V\) verlässt, zu einer zeitlichen Abnahme der Gesamtladung im Volumen \(V\) führt. Elektrische Ladung kann also immer nur über Ströme einen Raumbereich verlassen, aber nie einfach so spurlos verschwinden.
In differentieller Schweibweise lautet diese Gleichung:
| \[ \frac{d\rho}{dt} + \mathrm{div} \, \boldsymbol{j} = 0 \] |
Wenn also ein sehr kleiner Raumbereich eine Quelle für die Stromdichte darstellt (das ergibt den Term \( \mathrm{div} \, \boldsymbol{j} \)), so nimmt dort die elektrische Ladungsdichte \( \rho \) ab.
Schauen wir uns dazu noch einmal das Ampèresche Gesetz von oben an: \[ \mathrm{rot} \, \boldsymbol{B} = \mu_0 \, \boldsymbol{j} + \mu_0 \epsilon_0 \, \frac{d\boldsymbol{E}}{dt} \] Wie oben bereits erwähnt, kann man den zweiten Term rechts leicht übersehen und denkt nur daran, dass Ströme ein Magnetfeld erzeugen.
Angenommen, es gäbe den zweiten Term nicht und wir hätten nur die Gleichung \[ \mathrm{rot} \, \boldsymbol{B} = \mu_0 \, \boldsymbol{j} \] d.h. nur Ströme würden Magnetfelder erzeugen. Wenn wir nun die Divergenz links und rechts bilden, so ist links \[ \mathrm{div} \, (\mathrm{rot} \, \boldsymbol{B}) = 0 \] und wir erhalten rechts \[ \mathrm{div} \, \boldsymbol{j} = 0 \] Es gäbe dann keine Quellen für die Stromdichte und nach der Kontinuitätsgleichung müsste \[ \frac{d\rho}{dt} = 0 \] gelten. Die Ladungsdichte müsste zeitlich konstant bleiben – das ist genau der statische Fall, bei dem sich Ladungsdichten, Ströme und Felder zeitlich nicht ändern.
Im dynamischen Fall müssen wir jedoch den zweiten Term \(\mu_0 \epsilon_0 \, \frac{d\boldsymbol{E}}{dt}\) berücksichtigen, denn dann ergibt die Divergenz der Gleichung rechts den Zusatzterm \[ \mu_0 \epsilon_0 \, \mathrm{div} \, \frac{d\boldsymbol{E}}{dt} = \] \[ = \mu_0 \epsilon_0 \, \frac{d}{dt} \, \mathrm{div} \, \boldsymbol{E} = \] \[ = \mu_0 \epsilon_0 \, \frac{d}{dt} \, \frac{1}{\epsilon_0} \rho = \] \[ = \mu_0 \frac{d \rho}{dt} \] wobei wir die Maxwellgleichung \( \mathrm{div} \, \boldsymbol{E} = \rho/\epsilon_0 \) verwendet haben. Wir erhalten damit die Kontinuitätsgleichung \( d\rho/dt + \mathrm{div} \, \boldsymbol{j} = 0 \) als Folge der Maxwellgleichungen. Umgekehrt ist der zweite Term rechts im Ampèreschen Gesetz notwendig, um die Kontinuitätsgleichung sicherzustellen. Ein sich änderndes elektrisches Feld muss ein Magnetfeld erzeugen, damit die Ladungserhaltung gilt.
elektromagnetische Potentiale:
In der klassischen Physik sind elektrische und magnetische Felder die geeigneten Größen, um elektromagnetische Phänomene zu beschreiben, denn mit ihnen lässt sich die Kraft auf eine kleine Probeladung in Newtons Bewegungsgesetz direkt berechnen.
In der Quantentheorie wird die Beschreibung der Bewegung durch eine Bahnkurve durch eine Wellenbeschreibung ersetzt, so dass der Kraftbegriff seine Bedeutung verliert. An seine Stelle tritt eine Beschreibung, wie sich Frequenz und Wellenlänge im elektromagnetischen Feld verändern.
Nun hängt in der Quantentheorie die Frequenz mit der Teilchenenergie und die Wellenlänge mit dem Teilchenimpuls zusammen. Die elektrische Energie ist wiederum mit dem elektrischen Potential und der Impuls mit dem sogenannten Vektorpotential verknüpft. Daher beschreibt man elektromagnetische Phänomene in der Quantentheorie am Besten mithilfe der elektromagnetischen Potentiale an Stelle der Felder. Nur so kann man eine lokale Beschreibung beibehalten (Details dazu siehe Zusatzinfos zu Kapitel 5.3, speziell auch den Aharanov-Bohm-Effekt).
Vektorpotential:
Da es keine magnetischen Ladungen gibt, also \[ \mathrm{div} \, \boldsymbol{B} = 0 \] gilt, ist das Magnetfeld \( \boldsymbol{B} \) ein reines Wirbelfeld ohne Quellen. Ein solches Wirbelfeld kann man immer als Wirbelstärke eines Vektorpotentials \( \boldsymbol{A} \) schreiben:
| \[ \boldsymbol{B} = \mathrm{rot} \, \boldsymbol{A} \] |
denn umgekehrt ist dann die Divergenz eines solchen Rotationsfeldes immer automatisch Null: \[ \mathrm{div} \, \boldsymbol{B} = \mathrm{div} \, (\mathrm{rot} \, \boldsymbol{A}) = 0 \]
elektrisches Potential:
Wenn man in Faradays Induktionsgesetz \[ \mathrm{rot} \, \boldsymbol{E} = - \frac{d\boldsymbol{B}}{dt} \] das Magnetfeld als \( \boldsymbol{B} = \mathrm{rot} \, \boldsymbol{A} \) schreibt und alle Terme nach links bringt, so erhält man \[ \mathrm{rot} \left( \boldsymbol{E} + \frac{d\boldsymbol{A}}{dt} \right) = 0 \] d.h. der Term \( \boldsymbol{E} + \frac{d\boldsymbol{A}}{dt} \) in der Klammer ist ein wirbelfreies Feld und lässt sich demnach als Gradient (Steigung) eines skalaren (elektrischen) Potentials \( \Phi \) schreiben: \[ \boldsymbol{E} + \frac{d\boldsymbol{A}}{dt} = - \mathrm{grad} \, \Phi \] (das Minuszeichen ist reine Konventionssache). Meist stellt man diese Gleichung noch nach \(\boldsymbol{E}\) frei:
| \[ \boldsymbol{E} = - \mathrm{grad} \, \Phi - \frac{d\boldsymbol{A}}{dt} \] |
Eichtransformation der Potentiale:
Die beiden Potentiale sind nicht eindeutig. So kann man zum Vektorpotential \( \boldsymbol{A} \) ein beliebiges wirbelfreies Feld hinzuaddieren (oder subtrahieren), ohne die Wirbelstärke von \( \boldsymbol{A} \) und damit das Magnetfeld \( \boldsymbol{B} \) zu ändern. Ein solches wirbelfreies Zusatzfeld kann man immer als Gradient eines skalaren Feldes \(\chi\) schreiben. Das Vektorpotential \[ \boldsymbol{A}' := \boldsymbol{A} - \mathrm{grad} \, \chi \] ist also in Bezug auf das Magnetfeld gleichwertig zu \(\boldsymbol{A}\). So etwas nennt man eine Eichtransformation. Um durch die Eichtransformation auch das elektrische Feld nicht zu verändern, müssen wir das elektrische Potential ebenfalls transformieren, und zwar nach der Formel \[ \Phi' := \Phi + \frac{d\chi}{dt} \] mit demselben skalaren Feld \(\chi\), denn dann heben sich die beiden \(\chi\)-Terme in der Formel \( \boldsymbol{E} = - \mathrm{grad} \, \Phi - d\boldsymbol{A}/dt \) gegenseitig auf. Eichtransformationen spielen eine zentrale Rolle bei der Formulierung des Standardmodells. Mehr dazu siehe Kapitel 5.3.
Letztlich ist die Form der Maxwellgleichungen durch die spezielle Relativitätstheorie bestimmt (siehe Kapitel 3.2). Es kommt zu einem Wechselspiel von relativistischer Längenkontraktion, Zeitdilatation und der konsistenten Beschreibung einer physikalischen Situation durch unterschiedliche elektrische und magnetische Felder, je nach Bezugssystem. Feynman betrachtet dazu in seinen Feynman Vorlesungen über Physik, Band 2: Elektromagnetismus und Struktur der Materie, Kap. 13-6 folgendes Beispiel:
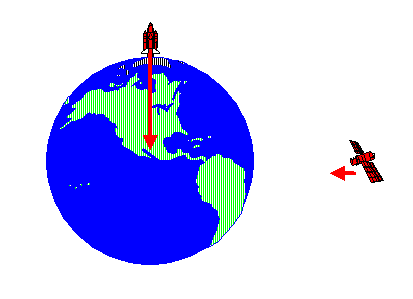
In einem ruhenden unendlich langen elektrisch neutralen Draht fließt ein elektrischer Strom, denn es bewegen sich alle Elektronen im Draht mit der Geschwindigkeit \(v\) nach rechts. Zugleich befindet sich außerhalb des Drahtes in gewissem Abstand ein einzelnes Elektron, das sich mit derselben Geschwindigkeit \(v\) ebenfalls nach rechts bewegt, parallel zum Draht. Der elektrische Strom im ruhenden Draht erzeugt ein ringförmiges Magnetfeld um den Draht, so dass auf das bewegte Elektron außerhalb des Drahtes eine Lorentzkraft wirkt, die das Elektron in Richtung Draht zieht (siehe Bild unten links).
Wie sieht dieselbe Situation aus, wenn man sich mit den Elektronen im und außerhalb des Drahtes mitbewegt, so dass sowohl das einzelne Elektron außerhalb des Drahtes als auch die Elektronen im Draht ruhend erscheinen? Nach Einstein muss auch die Physik in diesem Bezugssystem von denselben Maxwellgleichungen beschrieben werden wie die Physik im Bezugssystem, in dem der Draht ruht. Da sich das Einzel-Elektron außen nun nicht mehr bewegt, nimmt es von einem Magnetfeld keine Notiz mehr, d.h. die Lorentzkraft ist Null. Dennoch sollte es in Richtung Draht gezogen werden, denn es handelt sich ja um dieselbe Situation wie vorher, nur aus einem anderen Bezugssystem heraus betrachtet. Was also zieht das Elektron nun zum Draht hin?
Es stellt sich heraus, dass der Draht in diesem neuen Bezugssystem nicht mehr elektrisch neutral ist, sondern positiv elektrisch geladen, d.h. im neuen Bezugssystem übernimmt ein elektrisches Feld die Funktion, die zuvor ein Magnetfeld ausgeübt hat.
Der Grund für die elektrische Ladung des Drahtes im neuen Bezugssystem ist die relativistische Längenkontraktion: Der Abstand \(L\) zwischen zwei ruhenden Ladungen schrumpft im Bezugssystem, in dem sich die Ladungen mit der Geschwindigkeit \(v\) in Abstandsrichtung bewegen, auf den kleineren Abstand \[ L' = \frac{L}{\gamma} \] mit \[ \gamma = \frac{1}{\sqrt{1 - (v/c)^{2}}} \] (\(c\) ist die Lichtgeschwindigkeit). Die Ladungswerte selber ändern sich dabei nicht. Daraus folgt, dass eine ruhende Ladungsdichte \(\rho\) (Ladung pro Volumen) auf den Wert \[ \rho' = \gamma \, \rho \] anwächst, wenn man sie aus einem mit \(v\) bewegten Bezugsystem heraus betrachtet.
Die bewegte negative Ladungsdichte im ruhenden neutralen Draht nennen wir nun \( \rho_{-}' \) und die ruhenden positiven Gegenladungen der Atomkerne \(\rho_{+}\).
Im bewegten Bezugssystem ruht nun die negative Ladungsdichte (wir nennen sie entsprechend \( \rho_{-} \)), während die positive Gegenladungsdichte \( \rho_{+}' \) sich bewegt. Dabei gilt \[ \rho_{+}' = \gamma \, \rho_{+} \] \[ \rho_{-}' = \gamma \, \rho_{-} \] Der ruhende Draht soll nun elektrisch neutral sein: \[ \rho_{+} + \rho_{-}' = 0 \] Im bewegten Bezugssystem hat der Draht also die Ladungsdichte \[ \rho_{+}' + \rho_{-} = \] \[ = \gamma \, \rho_{+} + \frac{ \rho_{-}' }{\gamma} = \] \[ = \gamma \, \rho_{+} - \frac{ \rho_{+} }{\gamma} = \] \[ = \rho_{+} \, \left( \gamma - \frac{1}{\gamma} \right) = \] \[ = \rho_{+} \, \frac{(v/c)^{2}}{\sqrt{(1 - (v/c)^{2}}} \]
Anschaulich erscheint es zunächst merkwürdig, dass sich die bewegte Elektronen-Ladungsdichte
anders verhält als der ruhende Draht mit seiner positiven Gegenladung, wenn man zum bewegten Bezugssystem
übergeht. Die Elektronen müssten sich doch jeweils an derselben Stelle im Draht befinden, auch aus dem
bewegten Bezugssystem heraus gesehen.
Doch Vorsicht: die Elektronen bewegen sich gegenüber dem Draht. Man muss also in jedem Bezugssystem genau angeben, wann sie sich wo befinden. Und dieses WANN macht den Unterschied, denn beim Wechsel des Bezugssystems sind zuvor gleichzeitige Ereignisse nicht mehr gleichzeitig. Man betrachtet die Elektronen und die positiven Gegenladungen beim Bezugssystemwechsel nicht zu denselben Zeitpunkten wie vorher, wenn man dort jeweils ihre momentanen (also gleichzeitigen) Orte anschaut. Nur wenn man die Veränderungen in Raum und Zeit beide konsistent berücksichtigt, kann man die beschriebene Veränderung der Ladungsdichten verstehen. Details würden hier aber zu weit führen.
Man kann sich überlegen, dass die oben berechnete Ladungsdichte genau die richtige ist, um denselben physikalischen Effekt auf das einzelne Elektron hervorzurufen, den zuvor das Magnetfeld bewirkt hat (siehe Feynman). Das ist vielleicht überaschend, denn bei einer Geschwindigkeit von beispielsweise immerhin 3 km/s ist \[ v/c = 10^{- 5} \] und somit ziemlich genau \[ \frac{(v/c)^{2}}{\sqrt{(1 - (v/c)^{2}}} = 10^{- 10} \] Die positive Gesamt-Ladungsdichte \( \rho_{+}' + \rho_{-} \) des bewegten Drahtes entspricht also nur einem Zehnmilliardstel der positiven Gegenladungsdichte \( \rho_{+} \) im ruhenden Draht, die dort wiederum der Ladungsdichte der bewegten Elektronen entspricht.
Dennoch reicht diese geringe Ladung aus, um das einzelne Elektron ausreichend stark anzuziehen. Daran merkt man erneut, wie stark die elektromagnetische Wechselwirkung ist, beispielsweise im Vergleich zur bedeutungslosen Gravitationskraft, die vom Draht ausgeht. Der relativistische Effekt der Längenkontraktion, der bei kleinen Geschwindigkeiten noch sehr gering ist, führt nur wegen der enormen Stärke der elektromagnetischen Wechselwirkung zu gut beobachtbaren Effekten (und damit letztlich zu messbaren Magnetfeldern). Kein Wunder also, dass es die elektromagnetische Wechselwirkung war, die den Weg zu Einsteins spezieller Relativitätstheorie gewiesen hat.
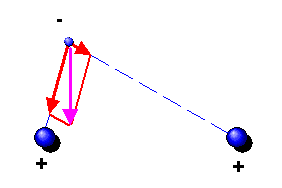
Man kann die obige Situation noch etwas abwandeln: Wir wollen die positive Gegenladung im Draht weglassen, also nur noch die negativen Elektronen betrachten. Im Bild rechts oben hätten wir es also mit einer ruhenden Kette von Elektronen mit Ladungsdichte \(\rho_{-}\) sowie einem einzelnen ruhenden Elektron neben der Kette zu tun. Da alle Ladungen ruhen, gibt es kein Magnetfeld.
Im Bild links würden sich dagegen Elektronenkette sowie Einzelelektron mit Geschwindigkeit \(v\) bewegen. Die bewegte Elektronenkette bildet einen elektrischen Strom und erzeugt ein Magnetfeld, das das ebenfalls bewegte Elektron zur Elektronenkette hinzieht. Im Gegenzug ist die Ladungsdichte dieser Elektronenkette gemäß \( \rho_{-}' = \gamma \, \rho_{-} \) angewachsen. Das Magnetfeld gleicht diese verstärkte elektrische Abstoßungskraft aus. Wichtig ist: Es hängt hier vom Bezugssystem ab, ob wir ein Magnetfeld sehen oder nicht. Das Magnetfeld wird gebraucht, um den relativistischen Effekt der Lorentzkontraktion für die Ladungsdichte der Elektronenkette auszugleichen. Das Magnetfeld ist also eine Konsequenz der speziellen Relativitätstheorie.
Betrachtet man die Maxwellgleichungen genauer, so stellt man fest, dass sie mit unseren normalen Vorstellungen von Raum und Zeit nicht zusammenpassen. Formal ausgedrückt: Die Maxwellgleichungen sind nicht invariant unter Galileitransformationen \[ \boldsymbol{x}' := \boldsymbol{x} - \boldsymbol{v} t \] (so dass man anschaulich in ein neues Bezugssystem wechselt, dass sich mit der Geschwindigkeit \(\boldsymbol{v}\) bewegt). Sie würden demnach nur in einem ausgezeichneten Ruhesystem gelten, nicht aber in dazu gleichförmig bewegten Bezugssystemen.
Ein Beispiel:
Oben hatten wir gesehen, dass elektromagnetische Wellen eine Lösung der Maxwellgleichungen ohne Ladungen und Ströme sind, und dass sie sich immer mit der Geschwindigkeit \[ c = \frac{1}{\sqrt{\epsilon_{0} \mu_{0}}} \] bewegen. Wenn wir nun mit der Geschwindigkeit \(v\) einer solchen Welle hinterherlaufen, so muss sich diese Welle in diesem neuen bewegten Bezugssystem mit der geringeren Geschwindigkeit \( c - v \) bewegen – zumindest nach den gängigen Vorstellungen, d.h. gemäß den Galileitransformationen.
Eine solche langsamere Welle ist keine Lösung der obigen Maxwellgleichungen mehr, d.h. die Maxwellgleichungen müssten in dem bewegten Bezugssystem anders aussehen als in dem unbewegten Bezugssystem, um elektromagnetische Wellen mit der Geschwindigkeit \( c - v \) zu erlauben. Es müsste sogar möglich sein, statische elektromagnetische Wellen zu beobachten, wenn man genau mit der Geschwindigkeit \(c\) hinterherläuft.
Das Problem ist nun: Solche statischen elektromagnetischen Wellen sind nie beobachtet worden. Stattdessen findet man im Experiment, dass die Maxwellgleichungen in jedem gleichförmig bewegten Bezugssystem (Inertialsystem) dieselbe Gestalt haben, mit denselben Feldkonstanten. Entsprechend haben elektromagnetische Wellen in jedem Inertialsystem dieselbe Geschwindigkeit, nämlich die Lichtgeschwindigkeit \(c\).
Also müssen unsere Vorstellungen über Raum und Zeit revidiert werden. Die Galileitransformationen können den Wechsel zwischen gleichförmig bewegten Bezugssystemen nicht korrekt beschreiben, und wir müssen andere Raum-Zeit-Transformationen finden, die die Form der Maxwellgleichungen und damit die Geschwindigkeit \(c\) elektromagnetischer Wellen unverändert lassen. Außerdem müssen diese Transformationen für kleine relative Geschwindigkeiten (gegenüber \(c\)) der Bezugssysteme in die Galileitransformationen übergehen. Diese Transformationen nennt man Lorentztransformationen (oder, wenn man Raum-Zeit-Translationen hinzunimmt, Poincarétransformationen).
Mathematisch beschreibt man eine Lorentztransformation durch eine reelle 4-mal-4-Matrix \(\Lambda\). Bei einem Wechsel des Inertialsystems fasst man dabei die Zeit \(t\) (multipliziert mit \(c\)) und die Raumkoordinaten \[ \boldsymbol{x} = \begin{pmatrix} x^1 \\ x^2 \\ x^3 \end{pmatrix} \] eines Inertialsystems zu einem vierdimensionalen Vektor (Vierervektor) \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} =: \begin{pmatrix} x^0 \\ \boldsymbol{x} \end{pmatrix} \] zusammen und berechnet die Raumzeit-Koordinaten in einem neuen Inertialsystem nach der Formel \[ x' := \Lambda \, x \] aus den alten Koordinaten. Die Koordinatenindizes haben wir dabei oben geschrieben, wobei wir die Zeitkoordinate \(ct\) als nullte Koordinate \[ x^{0} := ct \] bezeichnen.
Betrachten wir ein Lichtteilchen (Photon), dass sich mit Lichtgeschwindigkeit \(c\) in Richtung eines Einheitsvektors \(\boldsymbol{e}\) (mit \( |\boldsymbol{e}| = 1\)) bewegt, so dass sein Aufenthaltsort gleich \[ \boldsymbol{x} = ct \, \boldsymbol{e} \] ist. Also ist der Pfad (die sogenannte Weltlinie) für dieses Teilchen in der Raumzeit gegeben durch \[ x = \begin{pmatrix} ct \\ ct \, \boldsymbol{e} \end{pmatrix} = ct \, \begin{pmatrix} 1 \\ \boldsymbol{e} \end{pmatrix} \] und es gilt \[ g(x,x) := (x^{0})^{2} - \boldsymbol{x}^{2} = \] \[ = (ct)^{2} - (ct)^{2} \, \boldsymbol{e}^{2} = \] \[ = (ct)^{2} - (ct)^{2} = 0 \] Für eine Lorentztransformation \(\Lambda\) fordern wir nun, dass sie die Minkowskimetrik \[ g(x,y) := x^{0} y^{0} - \boldsymbol{x y} \] zweier Vierervektoren \(x\) und \(y\) nicht ändert: \[ g(\Lambda x,\Lambda y) = g(x,y) \] Denn dann gilt für unser Lichtteilchen bei einem Wechsel des Inertialsystems \( x' = \Lambda \, x \) die Gleichung \[ (ct')^{2} - (\boldsymbol{x}')^{2} = g(x',x') = g(x,x) = 0 \] also \[ (ct')^{2} = (\boldsymbol{x}')^{2} \] und somit \[ |\boldsymbol{x}'| = ct' \] d.h. auch in den neuen Koordinaten ist wieder die Bewegung des Lichtteilchens durch \[ \boldsymbol{x}' = ct' \, \boldsymbol{e}' \] gegeben – das Teilchen fliegt also wieder mit Lichtgeschwindigkeit, wenn auch möglicherweisein eine andere Richtung \( \boldsymbol{e}' \). Außerdem muss die Zeit \(t'\) im neuen Inertialsystem nicht dieselbe sein wie die Zeit \(t\) im alten Inertialsystem.
Weitere Details dazu habe ich in den Zusatzinfos zu Kapitel 3.2 (spezielle Relativitätstheorie) beschrieben. Hier noch eine nützliche Schreibweise, die Sie dort finden und die wir im Folgenden verwenden:
Wir bezeichnen Indizes 0 bis 3 mit griechischen Buchstaben, Indizes 1 bis 3 mit lateinischen Buchstaben: \[ x = (x^{\mu}) = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} \] \[ \boldsymbol{x} = (x^{i}) \] und summieren in allen Formeln über doppelte Indizs (Einsteinsche Summenkonvention), z.B. \[ \boldsymbol{x y} = x^{i} y^{i} \] Wir definieren die metrische 4-mal-4-Diagonalmatrix als \[ g = (g_{\mu\nu}) := \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \] und verwenden diese, um Indizes hoch- und runterzuziehen (mit Summenkonvention): \[ x_{\mu} := g_{\mu\nu} \, x^{\nu} \] so dass \[ x_{0} = x^{0} \] \[ x_{i} = - x^{i} \] ist. Damit ist \[ g(x,y) = x^{\mu} y^{\nu} g_{\mu\nu} = \] \[ = x_{\mu} y^{\mu} = x^{\mu} y_{\mu} = \] \[ = x^{0} y^{0} - \boldsymbol{x y} \] Die Matrixelemente von \(\Lambda\) schreiben wir als \( \Lambda^{\mu}_{\; \nu} \), so dass \[ (\Lambda x)^{\mu} = \Lambda^{\mu}_{\; \nu} \, x^{\nu} \] ist. Die Bedingung \[ g(\Lambda x,\Lambda y) = g(x,y) \] wird dann zur Bedingung \[ g_{\mu\nu} \, \Lambda^{\mu}_{\; \rho} \, \Lambda^{\nu}_{\; \sigma} = g_{\rho\sigma} \] Wir können nun die Maxwellgleichungen in diese Schreibweise übersetzen. Dazu fassen wir das elektrische und das magnetische Feld zu einer 4-mal-4-Matrix (dem Feldstärketensor) \( F = (F^{\mu\nu}) \) zusammen: \[ F = (F^{\mu\nu}) = \frac{1}{c} \cdot \begin{pmatrix} 0 & -\boldsymbol{E} \\ -\boldsymbol{E} & B \end{pmatrix} \] Dabei ist \( \boldsymbol{E} \) der dreikomponentige elektrische Feldvektor und \[ B = (B^{ij}) \] ist eine 3-mal-3-komponentige schiefsymmetrische Matrix, die die Komponenten des magnetischen Feldes \( \boldsymbol{B} = (B^{k}) \) enthält, so dass \[ B^{12} = - B^{3} \] ist (usw. zyklisch) und die Gleichung \[ B \, \boldsymbol{v} = \boldsymbol{v} \times \boldsymbol{B} \] gilt.
Die Bewegungsgleichung für ein elektrisch geladenes Teilchen lautet dann
| \[ \frac{dp^{\mu}}{d\tau} = Q \, F^{\mu\nu} \, u_{\nu} \] |
mit der Eigenzeit \(\tau\) (das ist die Zeit auf einer Uhr, die mit dem Teilchen mitfliegt) mit \[ d\tau = \frac{dt}{\gamma} \] mit dem Lorentzfaktor \[ \gamma = \frac{1}{\sqrt{1 - (v/c)^{2}}} \] und der Vierergeschwindigkeit \[ u = (u^{\mu}) = \frac{dx}{d\tau} = \begin{pmatrix} \gamma c \\ \gamma \boldsymbol{v} \end{pmatrix} \] und mit dem Viererimpuls \[ p = m \, u = \begin{pmatrix} E/c \\ \boldsymbol{p} \end{pmatrix} \] Hier ist \(E\) die relativistische Energie (nicht zu verwechseln mit dem elektrischen Feld \( \boldsymbol{E} \)) und \( \boldsymbol{p} \) ist der übliche räumliche Teilchenimpuls. Details dazu siehe Zusatzinfos zu Kapitel 3.2.
Überprüfen wir, ob die Gleichung \[ \frac{dp^{\mu}}{d\tau} = Q \, F^{\mu\nu} \, u_{\nu} \] tatsächlich die bekannte Bewegungsgleichung ergibt, wobei wir auf den Vorzeichenwechsel beim Hochziehen des Indexes von \(u_{\nu}\) für die räumlichen Komponenten achten müssen:
Die Gleichung für \( \mu = 0 \) ergibt: \[ \frac{dp^0}{d\tau} = \frac{d(E/c)}{d\tau} = \gamma \, \frac{dE}{c \, dt} = \] \[ = Q \, F^{0 k} \, u_{k} = \] \[ = Q \, \frac{1}{c} \, (- \boldsymbol{E}) (- \boldsymbol{u}) = \] \[ = Q \, \frac{1}{c} \, \gamma \, \boldsymbol{E \, v} \] und somit \[ \frac{dE}{dt} = Q \, \boldsymbol{E \, v} \] (wobei links die Teilchenenergie \(E\) und rechts das elektrische Feld \( \boldsymbol{E} \) steht).
Die Gleichung für \( \mu = k = 1, 2, 3 \) ergibt: \[ \frac{d p^k}{d\tau} = = \gamma \frac{d p^k}{dt} = \] \[ = Q \, F^{k\nu} \, u_{\nu} = \] \[ = Q \, F^{k0} \, u_{0} + Q \, F^{kl} \, u_{l} = \] \[ = Q \, \frac{\boldsymbol{E}^k}{c} \, \gamma c + Q \, B^{kl} \, (\gamma \, v_{l}) = \] \[ = Q \, \gamma \, \boldsymbol{E}^k + Q \, \gamma \, (\boldsymbol{v} \times \boldsymbol{B})^k \] und somit \[ \frac{d \boldsymbol{p}}{dt} = Q \, \boldsymbol{E} + Q \, \boldsymbol{v} \times \boldsymbol{B} \] Diese zweite Gleichung repräsentiert die bekannte Kraft auf ein elektrisch geladenes Teilchen, und die obere erste Gleichung \[ \frac{dE}{dt} = Q \, \boldsymbol{E \, v} \] ist die zur Impulsänderung zugehörige Energieänderung, denn \[ Q \, \boldsymbol{E \, v} = \boldsymbol{F}_{el} \, \frac{d \boldsymbol{x}}{dt} = \frac{dE}{dt} \] (nur die elektrische Kraft \( \boldsymbol{F}_{el} = Q \, \boldsymbol{E} \) ändert die Energie, nicht aber die magnetische Kraft, da diese immer senkrecht zur Bewegungsrichtung wirkt).
Die Gleichung \[ \frac{dp^{\mu}}{d\tau} = Q \, F^{\mu\nu} \, u_{\nu} \] ist also lediglich eine andere Schreibweise für die bisher bereits bekannte Gleichung \[ \frac{d \boldsymbol{p}}{dt} = Q \, \boldsymbol{E} + Q \, \boldsymbol{v} \times \boldsymbol{B} \] und die zugehörige Energieänderung. Die neue Schreibweise hat aber den Vorteil, dass sie mit Größen formuliert ist, die alle ein sehr einfaches Transformationsverhalten bei Lorentztransformationen \( x' := \Lambda x \) aufweisen, denn es gilt:
| \[ u' = \Lambda u \] \[ p' = \Lambda p \] \[ F'(x') = (\Lambda \circ \Lambda) \, F(x) \] |
wobei die letzte Gleichung für \[ (F')^{\mu\nu}(x') = \Lambda^{\mu}_{\; \rho} \, \Lambda^{\nu}_{\; \sigma} \, F^{\rho\sigma}(x) \] steht (mit Summenkonvention) und damit das Transformationsverhalten von \( \boldsymbol{E} \) und \( \boldsymbol{B} \) übersichtlich zusammenfasst.
Für die Vierergeschwindigkeit \( u \) folgt dieses Transformationsgesetz unmittelbar aus der Definition \[ u = \frac{dx}{d\tau} \] wobei \(\tau\) ein lorentzinvarianter Kurvenparameter (die Eigenzeit) ist, denn \(u\) ist lorentzinvariant normiert: \[ g(u,u) = c^{2} \] siehe siehe Zusatzinfos zu Kapitel 3.2 ).
Für den Viererimpuls \( p \) folgt das Transformationsgesetz aus der Definition \[ p = m u \] wobei \(m\) die lorentzinvariante Ruhemasse ist.
Für den Feldstärketensor \[ F = (F^{\mu\nu}) \] folgt das Transformationsgesetz aus den Maxwellgleichungen und der Forderung, dass sich die Lichtgeschwindigkeit bei Lorentztransformationen nicht ändern soll (mehr dazu gleich).
Und für die elektrische Ladung \(Q\) müssen wir die Invarianz bei Lorentztranformationen hier als Zusatzinfo hineinstecken. Das ist ein experimentelles Ergebnis: Nur so sind elektromagnetische Kraft und Maxwellgleichungen lorentzinvariant, gelten also in allen Inertialsystemen, wie es das Experiment zeigt. Mehr dazu weiter unten.
In der neuen Schreibweise ist unmittelbar erkennbar, dass die Gleichung ihre Form bei Lorentztransformationen nicht ändert, denn gilt die Gleichung für die ungestrichenen Größen, so gilt sie auch für die transformierten (gestrichenen) Größen.
Das sieht man in der alten Schweibweise mit \( \boldsymbol{E} \) und \( \boldsymbol{B} \) nicht sofort, sondern man muss es mühevoll nachrechnen. Dabei ist in der neuen Schreibweise wichtig, dass der Index \(\nu\) einmal oben und einmal unten steht, so dass er sich genauso verhält wie in \( g(x,y) = x^{\nu} y_{\nu} \), wobei \( g(\Lambda x,\Lambda y) = g(x,y) \) gilt (d.h. die Lorentzmatrix fällt beim \(\nu\) -Index weg).
Nun müssen wir nur noch die Maxwellgleichungen in die neue Schweibweise umformen. Dazu fassen wir Ladungsdichte \(\rho\) und Stromdichte \(\boldsymbol{j}\) zur Viererstromdichte
| \[ j := (j^{\mu}) = \begin{pmatrix} c \, \rho \\ \boldsymbol{j} \end{pmatrix} \] |
zusammen. Die Kontinuitätsgleichung \( d\rho/dt + \mathrm{div} \, \boldsymbol{j} = 0 \) lautet dann
| \[ \partial_{\mu} j^{\mu}(x) = 0 \] |
Dabei ist \[ \partial_{\mu} := \frac{\partial}{\partial x^{\mu}} \] also \[ \partial_{0} := \frac{1}{c} \, \frac{d}{dt} \] \[ \partial_{k} := \frac{\partial}{\partial x^{k}} \] Nun haben wir oben gesehen, dass die Kontinuitätsgleichung eine Folge der Maxwellgleichungen ist. Wenn nun die Maxwellgleichungen in jedem Inertialsystem gelten sollen, so muss dies auch für die Kontinuitätsgleichung gelten. Daraus können wir ablesen, dass sich die Viererstromdichte bei Bezugssystemwechsel wie ein Vierervektorfeld transformieren muss:
| \[ j'(x') = \Lambda \, j(x) \] mit \[ x' = \Lambda x \] oder gleichwertig dazu \[ j'(x) = \Lambda \, j(\Lambda^{-1} x) \] |
Man kann nun mithilfe dieses Transformationsgesetzes leicht nachrechnen: Wenn \( j(x) \) die Kontinuitätsgleichung erfüllt, so gilt das auch für \( j'(x) \).
Da die Kontinuitätsgleichung in jedem Inertialsystem gilt, ändert sich die elektrische Ladung eines Teilchens bei Bezugssystemwechsel nicht, wie wir es oben bereits verwendet haben. Die Ladungsdichte kann sich dagegen durchaus ändern, insbesondere aufgrund der Lorentzkontraktion – dies hatten wir oben in Abschnitt d) bereits verwendet. Auch die Stromdichte wird sich ändern. Beide zusammen werden durch einen Vierervektor beschrieben, dessen Transformationseigenschaften die Lorentzkontraktion und Zeitdilatation geeignet kompensieren, so dass die elektrische Ladung selbst sich nicht ändert.
Im Detail sieht das so aus:
Angenommen, wir hätten eine kleine kompakte ruhende Ladungsdichtewolke vor uns, z.B. eine geladene Kugelwolke. Die Viererstromdichte \( j \) transformiert sich beim Bezugssystemwechsel nun genauso wie die Vierergeschwindigkeit \( u \) dieser Ladungsdichte, so dass wir \[ j = \rho_{0} \, u \] schreiben können. Dabei ist \(\rho_{0}\) die Ladungsdichte der Wolke im Ruhesystem, denn dort ist \[ j = \rho_{0} \, u = \rho_{0} \, \begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix} = \begin{pmatrix} c \, \rho_{0} \\ \boldsymbol{0} \end{pmatrix} \] Betrachtet man nun die Ladungswolke aus einem bewegten Bezugssystem heraus, so dass sie sich mit der Geschwindigkeit \( \boldsymbol{v} \) bewegt, so ist die Vierergeschwindigkeit des Teilchens dort gleich \[ u = \begin{pmatrix} \gamma \, c \\ \gamma \boldsymbol{v} \end{pmatrix} \] und die Stromdichte wird gleich \[ j = \begin{pmatrix} c \, \rho \\ \boldsymbol{j} \end{pmatrix} = \] \[ = \rho_{0} \, u = \begin{pmatrix} \gamma \, \rho_{0} \, c \\ \gamma \, \rho_{0} \, \boldsymbol{v} \end{pmatrix} \] Die Ladungsdichte \( \rho \) der bewegten Ladungswolke ist also gleich \[ \rho = \gamma \rho_{0} \] d.h. die ruhende Ladungsdichte wird mit dem Faktor \(\gamma\) multipliziert. Genau dies kennen wir bereits aus Abschnitt d) (siehe oben). Die Stromdichte ist dabei gegeben durch \[ \boldsymbol{j} = \rho \, \boldsymbol{v} = \gamma \rho_{0} \boldsymbol{v} \] Zum Vergleich die Gravitation:
Wie wird die relativistische Beschreibung von Gravitationsquellen in der allgemeinen Relativitätstheorie aussehen? Coulomb-Gesetz und Newtons Gravitationsgesetz sehen ja praktisch gleich aus, nur dass die Ladung durch die Masse ersetzt wird.
Aber: elektrische Ladungen sind auch in der Relativitätstheorie erhalten, Massen dagegen nicht! Daher ist in der allgemeinen Relativitätstheorie nicht die Masse, sondern die relativistische Gesamtenergie eine Quelle der Gravitation (siehe Zusatzinfos zu Kapitel 7.1).
Anders als die elektrische Ladung ändert sich die Energie aber beim Wechsel des Bezugssystems, denn sie ist die Null-Komponente des Viererimpulsvektors.
Geht man nun vom Viererimpuls zu einer Viererimpulsdichte über (so wie man von Ladungen zur el. Stromdichte übergeht), so braucht man zur deren relativistischer Beschreibung ein Objekt mit zwei Indices: Ein Index hat seinen Ursprung im Viererimpuls, und der zweite Index kommt daher, dass wir zu Viererimpuls-Stromdichten übergehen (analog entsteht ein Index, wenn wir von der elektrischen Ladung zur elektrischen Viererstromdichte übergehen). Statt von der Viererimpuls-Stromdichte spricht man auch vom Energie-Impuls-Tensor.
Mithilfe des Feldstärketensors und der Viererstromdichte kann man nun die beiden Maxwellgleichungen \[ \mathrm{div} \, \boldsymbol{E} = \frac{\rho}{\epsilon_{0}} \] \[ \mathrm{rot} \, \boldsymbol{B} = \mu_0 \, \boldsymbol + \frac{1}{c^{2}} \frac{d\boldsymbol{E}}{dt} \] folgendermaßen zusammenfassen (wobei wir \( \mu_0 \epsilon_0 = 1/c^{2} \) verwenden):
| \[ \partial_{\mu} F^{\mu\nu} = \mu_{0} \, j^{\nu} \] |
Kurze Kontrollrechnung:
\( \nu = 0 \) ergibt: \[ \mathrm{div} \, \boldsymbol{E}/c = \mu_{0} c \, \rho \] und somit \[ \mathrm{div} \, \boldsymbol{E} = \mu_{0} c^{2} \rho = \frac{\rho}{\epsilon_{0}} \] \( \nu = 1, 2, 3 \) ergibt: \[ \frac{1}{c} \frac{d}{dt} \, (- \boldsymbol{E}/c) + \mathrm{rot} \, \boldsymbol{B} = \mu_{0} \, \boldsymbol{j} \] und somit \[ \mathrm{rot} \, \boldsymbol{B} = \mu_{0} \, \boldsymbol{j} + \frac{1}{c^{2}} \frac{d\boldsymbol{E}}{dt} \] Passt also! Die relativistische Schreibweise der Maxwellgleichungen erlaubt es zudem, direkt die Kontinuitätsgleichung abzuleiten, indem wir \( \partial_{\nu} \) auf sie anwenden (und über \(\nu\) summieren): \[ \partial_{\nu} \partial_{\mu} F^{\mu\nu} = \mu_{0} \, \partial_{\nu} j^{\nu} \] Wenn wir links in der Summe die Indices \(\mu\) und \(\nu\) ineinander umbenennen und die Antisymmetrie von \(F^{\mu\nu}\) verwenden, so sehen wir, dass der Term links gleich Null sein muss, so dass auch \[ \delta_{\nu} j^{\nu} = 0 \] gilt.
Wie sieht es mit den beiden anderen Maxwellgleichungen \[ \mathrm{div} \, \boldsymbol{B} = 0 \] \[ \mathrm{rot} \, \boldsymbol{E} = - \frac{d\boldsymbol{B}}{dt} \] aus? Diese beiden Gleichung schreiben wir dazu etwas um, so dass sie den anderen beiden Gleichungen möglichst ähnlich werden: \[ \mathrm{div} \, (c \, \boldsymbol{B}) = 0 \] \[ \mathrm{rot} \, (- \boldsymbol{E}/c) = \frac{1}{c^{2}} \frac{d(c\boldsymbol{B})}{dt} \] Damit ist klar: Wir erhalten diese beiden Gleichungen, wenn wir in den beiden anderen Gleichungen \[ \mathrm{div} \, \boldsymbol{E} = \mu_{0} c^{2} \rho = \frac{\rho}{\epsilon_{0}} \] \[ \mathrm{rot} \, \boldsymbol{B} = \mu_{0} \, \boldsymbol{j} + \frac{1}{c^{2}} \frac{d\boldsymbol{E}}{dt} \] von oben Ladungs- und Stromdichte Null setzen sowie darin \( \boldsymbol{B} \) durch \( - \boldsymbol{E}/c \) und \( \boldsymbol{E} \) durch \( c \boldsymbol{B} \) ersetzen. Diese Ersetzung müssen wir also auch im Feldstärketensor vornehmen – den so entstehenden neuen dualen Feldstärketensor nennen wir \( \tilde{F} \):
| \[ \tilde{F} = (\tilde{F}^{\mu \nu}) = \begin{pmatrix} 0 & -\boldsymbol{B} \\ \boldsymbol{B} & -E/c \end{pmatrix} \] |
wobei unten rechts wieder die entsprechende schiefsymmetrische Matrix \( E \) steht. Die beiden Maxwellgleichungen \( \mathrm{div} \, \boldsymbol{B} = 0 \) und \( \mathrm{rot} \, \boldsymbol{E} = - d\boldsymbol{B}/dt \) lauten dann also:
| \[ \partial_{\mu} \tilde{F}^{\mu\nu} = 0 \] |
Die Gleichung ermöglicht es, die Felder \( \boldsymbol{E} \) und \( \boldsymbol{B} \) als Ableitungen des elektrischen Potentials \( \Phi \) und des Vektorpotentials \( \boldsymbol{A} \) zu schreiben (siehe oben): \[ \boldsymbol{B} = \mathrm{rot} \, \boldsymbol{A} \] \[ \boldsymbol{E} = - \mathrm{grad} \, \Phi - \frac{d\boldsymbol{A}}{dt} \] Auch hierfür können wir eine relativistische Schreibweise angeben, indem wir das Viererpotential
| \[ A := (A^{\mu}) = \begin{pmatrix} \Phi/c \\ \boldsymbol{A} \end{pmatrix} \] |
einführen, denn dann kann man diese beiden Gleichungen zusammenfassen zu:
| \[ F^{\mu\nu} = \partial^{\mu} A^{\nu} - \partial^{\nu} A^{\mu} \] |
mit \[ \partial^{0} = \partial_{0} = \frac{1}{c} \frac{d}{dt} \] \[ \partial^{k} = - \partial_{k} = - \frac{\partial}{\partial x^{k}} \] So ist beispielsweise \[ F^{0k} = - E^{k}/c = \partial^{0} A^{k} - \partial^{k} A^{0} = \] \[ = \frac{1}{c} \frac{d}{dt} A^{k} + \frac{\partial}{\partial x^{k}} \Phi/c \] was wie gewünscht die Gleichung \[ \boldsymbol{E} = - \mathrm{grad} \, \Phi - \frac{d\boldsymbol{A}}{dt} \] ergibt.
Wenn man nun in den Maxwellgleichungen \[ \partial_{\mu} F^{\mu\nu} = \mu_{0} \, j^{\nu} \] den Feldstärketensor über \( F^{\mu\nu} = \partial^{\mu} A^{\nu} - \partial^{\nu} A^{\mu} \) durch das Viererpotential ausdrückt, so ergibt sich folgende Gleichung für das Viererpotential: \[ \partial_{\mu} \, \left( \partial^{\mu} A^{\nu} - \partial^{\nu} A^{\mu} \right) = \mu_{0} \, j^{\nu} \] Im zweiten Term links kann man nun die Ableitungen vertauschen (das Potential ist dafür gutartig genug): \[ \partial_{\mu} \partial^{\mu} A^{\nu} - \partial^{\nu} \partial_{\mu} A^{\mu} = \mu_{0} \, j^{\nu} \] Nun ist das Viererpotential nicht eindeutig bestimmt, denn auch das Viererpotential
| \[ (A')^{ \mu} := A^{\mu} + \partial^{\mu} \chi \] |
ergibt denselben Feldstärketensor wie \(A^{\mu}\), da der \(\partial^{\mu} \chi\)-Zusatzterm wegen der Vertauschbarkeit der Ableitungen wegfällt: \[ \partial^{\mu} \partial^{\nu} \chi - \partial^{\nu} \partial^{\mu} \chi = 0 \] Das ist genau die Eichtransformation der Potentiale, die wir oben bereits kennengelernt haben, nur jetzt in relativistischer Schreibweise. Damit ist es uns möglich, jedes Viererpotential so umzueichen, dass es die Bedingung \[ \partial_{\mu} A^{\mu} = 0 \] erfüllt (Lorentzeichung). In der Lorentzeichung lauten die Maxwellgleichungen dann (ausgedrückt durch das Viererpotential):
| \[ \partial_{\mu} \partial^{\mu} A^{\nu} = \mu_{0} \, j^{\nu} \] |
Dabei steht links der bekannte Wellenoperator \[ \partial_{\mu} \partial^{\mu} = \frac{1}{c^{2}} \frac{d^2}{dt^{2}} - \frac{\partial^2}{\partial \boldsymbol{x}^{2}} \] Im leeren Raum ohne Ladungen und Ströme (also \( j^{\nu} = 0 \)) ergibt sich damit für jede Komponente des Viererpotentials die Wellengleichung \[ \partial_{\mu} \partial^{\mu} A^{\nu} = 0 \] Wir sehen hier also unmittelbar, dass die Maxwellgleichungen im ladungsfreien Fall ebene Wellen als Lösungen haben, und zwar zunächst für die Potentiale und damit auch für die daraus abgeleiteten elektromagnetischen Felder. Diese Wellen bewegen sich in jedem gleichförmig bewegten Bezugssystem mit Lichtgeschwindigkeit.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 19 December 2023