Kapitel 3
Feynmans Pfad zur Quantenelektrodynamik

2  Das Meisterstück: Feynman-Diagramme und Antiteilchen

Zusammenfassung des Buchkapitels:

Gestörte Quantenwellen: nichtrelativistische Störungstheorie

Wie lässt sich die Quantenelektrodynamik in der Sprache der Pfade ausdrücken? Es gibt ein sehr nützliches Werkzeug, mit dem sich diese Frage systematisch angehen lässt: die sogenannte Störungstheorie. Die Idee dabei ist, dass man Wechselwirkungen schrittweise berücksichtigt.

Hier ein typisches Beispiel aus der nichtrelativistischen Quantenmechanik: ein sogenannter Streuprozess. Es beginnt mit einem Strahl freier Teilchen − sagen wir Elektronen − die wir durch eine nahezu ebene Quantenwelle beschreiben können. Diese geordnete Wellenform wird "gestört", wenn sie beispielsweise auf das elektrische Feld eines Atomkerns trifft. Es entstehen Streuwellen, die das Gebiet des Atomkerns nach allen Seiten hin verlassen. Sie entsprechen Elektronen, die vom Feld des Atomkerns aus ihrer Bahn geworfen wurden.

Problematisch für die Berechnung dieses Prozesses ist der Wechselwirkungsbereich, in dem das elektrische Feld wirkt und die Welle durcheinanderbringt. Das ist nun genau der Bereich, in dem die Störungstheorie ansetzt: Sie beschreibt den Einfluss des Feldes näherungsweise dadurch, dass dieses beim Durchlauf der Welle überall und ständig neue Elementarwellen entstehen lässt, die sich selbst wieder ungestört ausbreiten. Das nennt man die erste Ordnung der Störungstheorie.

Will man es genauer wissen, dann muss man berücksichtigen, dass auch die neu erzeugten Elementarwellen vom Feld beeinflusst werden. Nicht nur die ursprüngliche Welle, sondern auch die neuen Elementarwellen lassen dann überall weitere Elementarwellen entstehen, die sich wiederum ungestört ausbreiten. Das wäre dann die zweite Ordnung der Störungstheorie.

Natürlich lässt sich dieses Spiel immer weiter fortsetzen: Je genauer man sein möchte oder je stärker das störende Feld ist, umso mehr Ordnungen muss man berücksichtigen.

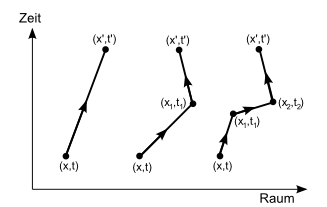
Um den Überblick zu behalten, kann man die Störungstheorie gut durch Raum-Zeit-Diagramme veranschaulichen. Gerade Linien kennzeichnen darin die Ausbreitung einer Elementarwelle von einem Raum-Zeit-Punkt zu einem anderen Raum-Zeit-Punkt. An Knickstellen (Vertices) entstehen neue Elementarwellen. Die Diagramme bis zur zweiten Ordnung sehen dann so aus:

Man kann sich die Linien auch als mögliche Teilchenbahnen vorstellen, und zwar ganz im Sinne von Feynmans Pfadintegralen. Jedes Diagramm stellt mögliche Pfade zwischen Start- und Zielpunkt dar: den Pfad ohne Knick, alle Pfade mit einem Knick, alle Pfade mit zwei Knicks und so fort, wobei die Knickpunkte überall im elektrischen Feld des Atomkerns liegen können. Zu jedem dieser Pfade gehört eine Quantenwelle, die nachher über alle Pfade inklusive aller möglichen Zwischenpunkte aufsummiert wird, um die Gesamt-Quantenwelle am Endpunkt auszurechnen. Der Vorteil der Störungstheorie liegt nun darin, dass man die entsprechenden Pfadamplituden sehr gut ausrechnen kann.

Störungstheorie in der QED: Feynman-Diagramme

Was ändert sich, wenn man zur Quantenelektrodynamik (QED) übergeht, bei der die Spezielle Relativitätstheorie zwingend dazugehört? Feynman widmete sich intensiv dieser Fragestellung und entwickelte entsprechende Raum-Zeit-Diagramme, die als Feynman-Diagramme weithin bekannt und berühmt geworden sind.

Als erstes musste Feynman dafür die klassischen elektromagnetischen Felder durch eine Quantenbeschreibung ersetzen, sodass eine neue Teilchensorte hinzukommt: Feldquanten, die beim Elektromagnetismus Photonen heißen. Die Knickstellen (Vertices) in den Wegen der Elektronen entstehen dann durch den Einfluss eines Photons, das an der Knickstelle emittiert oder absorbiert wird.

In den Diagrammen stellte Feynman die Elementarwelle eines Photons durch eine gewellte Linie dar. Eine Knickstelle (Vertex) sieht also jetzt so aus, dass dort immer eine gewellte Photonlinie abzweigt. Ein Vertex kennzeichnet damit die Stelle, an der die Elementarwelle eines Photons neu entsteht oder absorbiert wird.

Als nächstes musste Feynman herausfinden, wie die Elementarwellen der Elektronen und Photonen genau aussehen. Bei den Photonen erscheint das auf den ersten Blick relativ einfach: Die Elementarwellen sollten sich mit Lichtgeschwindigkeit ausbreiten, denn Photonen sind ja die Quanten des Lichts. Feynmans Berechnungen zeigten jedoch, dass diese Sichtweise nicht ganz zutrifft: Ein kleiner Teil der Elementarwelle ist etwas langsamer, ein anderer Anteil aber auch etwas schneller als Lichtgeschwindigkeit, wobei die Amplitude der Elementarwelle umso kleiner wird, je größer die Abweichung von der Lichtgeschwindigkeit ist.

Bei großen Entfernungen sind die Amplituden, schneller oder langsamer als Lichtgeschwindigkeit zu sein, sehr klein und entgegengesetzt gerichtet, sodass sie sich aufheben. Im subatomaren Bereich müssen wir allerdings die mögliche Abweichung von der Lichtgeschwindigkeit unbedingt berücksichtigen. Die Photonenlinien können im Feynmandiagramm entsprechend unterschiedliche Neigungswinkel aufweisen.

Dasselbe trifft auch auf Elektronen zu! Auch hier haben die entsprechenden Elementarwellen einen kleinen Anteil oberhalb der Lichtgeschwindigkeit. Das ist besonders zwischen zwei Vertices wichtig – hier kann die Linie im Diagramm auch sehr flach verlaufen, also schneller als mit Lichtgeschwindigkeit, so wie hier in Diagramm (c):

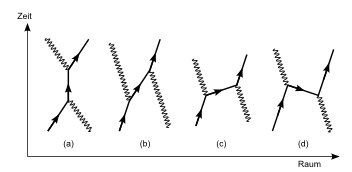
Für solche Verticeswie in Diagramm (c), deren räumlicher Abstand sich nur mit Überlichtgeschwindigkeit überbrücken lässt, macht die Spezielle Relativitätstheorie eine erstaunliche Aussage: Ihre zeitliche Reihenfolge lässt sich umdrehen, wenn man sie aus der Sicht eines Beobachters betrachtet, der sich hinreichend schnell in die richtige Richtung bewegt (Diagramm (d) ). Da nun alle Beobachter, die sich gleichförmig gegeneinander bewegen, nach Einstein vollkommen gleichberechtigt sind, gibt es keine absolut verbindliche zeitliche Reihenfolge der beiden Vertices.

Der Beobachter, der Diagramm (d) als korrekt betrachtet, sieht allerdings etwas Merkwürdiges: Für die Wegstrecke zwischen den beiden Vertices scheint das Elektron sich zeitlich rückwärts zu bewegen. Nur was soll das bedeuten? Ist so etwas überhaupt erlaubt?

Zurück in die Zukunft

Schon früher haben wir gesehen, dass es durchaus sinnvoll sein kann, auch die umgekehrte Zeitrichtung zuzulassen. Genau das hatten Feynman und Wheeler getan, als sie sich Gedanken über avancierte elektromagnetische Felder und Wellen machten, die rückwärts in der Zeit laufen. Die grundlegenden physikalischen Gesetze sind fast alle symmetrisch bezüglich der Zeitrichtung, unterscheiden also nicht zwischen Zukunft und Vergangenheit (bis auf eine seltene Ausnahme, die gewisse Teilchenzerfälle betrifft und die wir hier getrost ignorieren können) – eine Umkehr der Zeitrichtung erscheint also durchaus legitim.

In unseren Diagrammen können wir mithin durchaus Elektronen auch rückwärts in der Zeit laufen lassen. Allerdings stellt sich dann die Frage, was das für einen makroskopischen Beobachter bedeutet, dessen Zeitrichtung immer von der Vergangenheit in die Zukunft gerichtet ist. Was sieht er?

Warum es Antiteilchen gibt

Einen Hinweis liefert die Ladungserhaltung: Ein makroskopische Beobachter betrachtet den zeitlichen Ablauf immer streng in wachsender Zeitrichtung, also im Diagramm von unten nach oben. Er sieht in Diagramm (d) zunächst, wie sich ein Elektron von links und ein Photon von rechts aufeinander zubewegen. Vor dem Zusammentreffen verschwindet das elektrisch neutrale Photon plötzlich und erzeugt zwei Teilchenlinien, die weiter nach oben laufen. Die Linie rechts mit dem Pfeil nach oben ist ein weiteres negativ geladenes Elektron. Also muss nach der Ladungserhaltung die flache Linie in der Mitte mit dem Pfeil nach unten − das in der Zeit zurücklaufende Elektron – ein positiv geladenes Teilchen sein, wenn wir es in der normalen Zeitrichtung betrachten. Da es ansonsten einem Elektron gleicht, liegt die Vermutung nahe, dass es sich um ein Anti-Elektron – also ein Positron – handelt. Elektronen, die sich rückwärts in der Zeit bewegen, erscheinen also als Positronen, wenn wir sie in der normalen Zeitrichtung betrachten (mehr dazu in den Zusatzinfos unten). Beim nächsten Vertex oben links vernichten sich dann das Positron und das von links kommende ursprüngliche Elektron gegenseitig und ein Photon entsteht.

Materie und Antimaterie – der kleine Unterschied

Auch in unseren Feynman-Diagrammen können Elektronen und Positronen immer nur paarweise entstehen. Trotzdem gibt es heute in unserem Universum fast ausschließlich Elektronen und praktisch keine Positronen. Die Symmetrie zwischen Materie und Antimaterie kann also in der Realität nicht ganz so perfekt sein, wie sie die Diagramme andeuten. Die QED alleine kann das nicht erklären − hier braucht man weitergehende Theorien, und selbst heute ist diese Frage noch nicht endgültig geklärt.

Antiteilchen lösen das Problem der negativen Energien

Die Idee, dass Elektronen rückwärts in der Zeit laufen können, hat noch einen weiteren wichtigen Aspekt: Sie löst das Problem mit den negativen Energien, ohne dass dafür ein gefüllter Dirac-See erforderlich ist. Anstatt zu fordern, dass alle negativen Energiezustände besetzt sind, fordert man, dass die negativen Energiezustände genau diejenigen sind, die sich rückwärts in der Zeit bewegen, während sich die positiven Energiezustände wie gewohnt vorwärts in der Zeit bewegen. Ein Elektron, das sich rückwärts in der Zeit bewegt, hat also eine negative Energie.

Die Folge ist: Sobald das Energiekonto eines Elektrons ins Negative rutscht, wird es unserem Zugriff für die weitere Zukunft entzogen, indem es seine Reise in die Vergangenheit antritt. Wir können also nur ein einziges Mal den Energie-Dispokredit nutzen – danach verschwindet das Elektron mit seinem Energiekonto im Nebel der Vergangenheit.

Dort könnte nun jemand genau denselben Energiebetrag auf das Energiekonto einzahlen, den wir später daraus entnehmen. Er gleicht damit in der Vergangenheit die Energie-Schulden aus, die wir heute machen. Betrachten wir diesen Vorgang in der normalen Zeitrichtung, so sehen wir folgendes: Jemand zahlt in der Vergangenheit einen Energiebetrag auf das Energiekonto ein, den wir heute wieder entnehmen. Es ist genau so, als wäre in der Vergangenheit ein Energie-Guthaben auf das Konto eingezahlt worden, das wir heute wieder abheben. Energie-Schulden, die in die Vergangenheit reisen, wirken also genauso wie ein Energie-Guthaben, das in der normalen Zeitrichtung voranschreitet. Ein Elektron, das mit negativer Energie in die Vergangenheit reist, entspricht damit in der normalen Zeitrichtung einem Positron mit positiver Energie.

Feynman erhielt mit dieser Idee in seinen Rechnungen auf relativ einfache Weise dieselben Resultate wie andere Leute, die mit Löchern im Dirac-See jonglierten, was sehr viel komplizierter war.

Gib Stückelberg seine Notizen zurück!

Feynman und Wheeler waren übrigens nicht die einzigen, die auf diese Idee gekommen waren. Der Schweizer Mathematiker und Physiker Ernst Carl Gerlach Stückelberg hatte sie bereits im Jahr 1941vorgeschlagen, wobei Feynman dies wohl damals noch nicht wusste. Auch manch andere Idee zur QED nahm Stückelberg vorweg. Manche sagen sogar, Stückelberg sei seiner Zeit um Jahre voraus gewesen. Da er seine Arbeiten allerdings in eher unbekannten Journalen veröffentlichte und sie nur wenig propagierte, blieben sie weitgehend unbeachtet und wurden lange unterschätzt.

Feynmans Trickkiste

Mit seinen Raum-Zeit-Diagrammen hatte Feynman ein effektives Werkzeug an der Hand, um die Probleme der QED anzugehen. Die Linien und Vertices der Elektronen und Photonen vermittelten eine anschauliche Vorstellung von den physikalischen Prozessen und lieferten zugleich eine Rechenvorschrift, wie die einzelnen Quantenamplituden multipliziert und addiert werden mussten, um die Gesamtamplitude für den Prozess zu ermitteln.

Was jetzt noch fehlte, war eine echte Herausforderung für Feynmans Methode, bei der sie ihre Schlagkraft unter Beweis stellen konnte. Man brauchte ein experimentelles Resultat, das sich mit der Dirac-Gleichung alleine nicht erklären ließ. Und Feynman hatte Glück: Mit der Messung der sogenannten Lamb-Shift sowie der Bestimmung des anomalen magnetischen Moments des Elektrons sollten sich gleich zwei solche Ergebnisse einstellen, die dringend auf eine theoretische Erklärung warteten. Das war die Chance, auf die Feynman und viele andere Theoretiker gewartet hatten.

Zusatzinformationen:

a) Wheelers Geistesblitz: Wenn Elektronen in die Vergangenheit reisen

a) Wheelers Geistesblitz: Wenn Elektronen in die Vergangenheit reisen

Feynman berichtet in seinem Nobelpreisvortrag, wie ihn sein Doktorvater John Archibald Wheeler eines Tages aufgeregt in Princeton anrief und ihm von einer interessanten Idee erzählte, die Feynman später in anderer Form in seine Formulierung der QED übernahm:

"... I received a telephone call one day at the graduate college at Princeton from Professor Wheeler, in which he said, "Feynman, I know why all electrons have the same charge and the same mass" "Why?" "Because, they are all the same electron!" And, then he explained on the telephone, "suppose that the world lines which we were ordinarily considering before in time and space – instead of only going up in time were a tremendous knot, and then, when we cut through the knot, by the plane corresponding to a fixed time, we would see many, many world lines and that would represent many electrons, except for one thing. If in one section this is an ordinary electron world line, in the section in which it reversed itself and is coming back from the future we have the wrong sign to the proper time – to the proper four velocities – and that's equivalent to changing the sign of the charge, and, therefore, that part of a path would act like a positron."

Wheeler glaubte also zu wissen, warum alle Elektronen in der Welt dieselbe Ladung und Masse haben: Weil es immer dasselbe Elektron sei! Ein einziges Elektron könnte in der Zeit vor und zurück geworfen werden, sodass es mal in die Zukunft reist, dann wieder in die Vergangenheit. Sein Weg durch Raum und Zeit (seine Weltlinie oder englisch world line) wäre dann wie eine Zick-Zack-Linie oder wie ein riesiges Knäuel. Zu einer festen Zeit würden wir also immer wieder dasselbe Elektron sehen, mal aus der Vergangenheit kommend, mal aus der Zukunft. Dabei würde seine inner Uhr (seine sogenannte Eigenzeit oder englisch proper time) entlang der Zick-Zack-Weltline immer weiter fortschreiten.

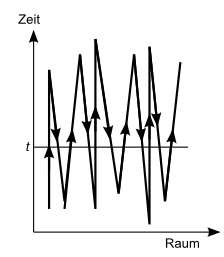
In den Bereichen der Weltlinie, in denen es aus der Zukunft kommt und rückwärts in der Zeit reist, würde seine innere Uhr nach Wheelers Idee also gegen die äußere Zeit laufen – seine Eigenzeit hätte relativ zur äußeren Zeit ein negatives Vorzeichen ("we have the wrong sign to the proper time"; in der Grafik ist die Richtung anwachsender Eigenzeit durch Pfeile dargestellt). Das würde bedeuten, dass auch die sogenannte Vierergeschwindigkeit (proper four velocity) sich umdreht und ihr Vorzeichen wechselt, und das sei gleichbedeutend damit, dass die Ladung des Elektrons ihr Vorzeichen wechselt. In den Bereichen, in denen das negativ geladene Elektron rückwärts in der Zeit fliegt, würde es sich also wie ein positiv geladenes Positron verhalten (das vorwärts in der Zeit fliegt).

Wie kam Wheeler auf diese Idee?

Um das zu verstehen, müssen wir einen Abstecher in die Spezielle Relativitätstheorie machen. Das Bild eines Elektrons, das in der Zeit zurück reist, macht nämlich erst dort wirklich Sinn. Nur in der Relativitätstheorie können wir verschiedene Zeitbegriffe voneinander unterscheiden. Eine innere Uhr, die das Elektron mit sich führt und die dessen Eigenzeit $\tau$ anzeigt, läuft nämlich in der Relativitätstheorie im Allgemeinen nicht unbedingt synchron zur Uhr eines äußeren Beobachters, der ruht oder sich gleichförmig bewegt.

Der äußere Beobachter sieht zu jeder Zeit $t$, die seine Uhr anzeigt, das Elektron an einem bestimmten Ort $$\mathit{x}=\left(\begin{array}{c}{x}^1\\ x^2\\ x^3\end{array}\right)$$ auf seiner Flugbahn, wobei in der Klammer die drei räumlichen Koordinaten des Elektrons zur Zeit $t$ stehen, die wir zu einem dreidimensionalen Raumvektor $\mathit{x}$ (fett gedruckt) zusammenfassen. Die drei Raumindizes schreiben wir dabei rechts oben, so wie in der Relativitätstheorie üblich ($x^2$ bedeutet also nicht x hoch 2, sondern ist einfach die zweite Raumkoordinate des Elektrons).

In der Relativitätstheorie bietet es sich an, neben den drei räumlichen Koordinaten auch die Zeit mit hinzuzunehmen und alle vier Größen zu einem einzigen Objekt zusammenzufassen, das man auch Vierervektor nennt. Damit alle vier Größen die Dimension einer Länge haben, multipliziert man die Zeit $t$ noch mit der Lichtgeschwindigkeit $c$. Man gibt in dem Vierervektor also an, wie weit ein Lichtstrahl in der Zeit $t$ gekommen wäre. Der Vierervektor lautet also:

Raum-Zeit-Vierervektor: $$x=\left(\begin{array}{c}ct\\ \mathit{x}\end{array}\right)=\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right)$$

Der zeitlichen Koordinate $x^0=ct$ gibt man dabei die Index-Nummer Null, die man wieder oben rechts notiert (so wie bei den drei räumlichen Koordinaten auch).

Wenn der äußere Beobachter zu jeder Zeit $t$ den zugehörigen Aufenthaltsort $\mathit{x}$ des Elektrons notiert und in einer Raum-Zeit-Grafik einträgt, so ergibt sich darin eine Kurve, die die Bewegung des Elektrons in Raum und Zeit (also in der Raumzeit) beschreibt – genau wie oben in der Grafik. Der Vierervektor $x$ des Elektrons beschreibt also eine Kurve in der Grafik und damit in der Raumzeit und stellt so dessen Bewegung dar, wie der äußere Beobachter sie sieht. Diese Raumzeit-Kurve ist die sogenannte Weltlinie des Elektrons.

Wir können nun in der Raum-Zeit-Grafik zusätzlich an jedem Raum-Zeit-Punkt $x$ die entsprechende Eigenzeit $\tau$ notieren, die auf der mitgeführten inneren Uhr des Elektrons am Ort $\mathit{x}$ zur Zeit $t$ angezeigt wird. Jeder Punkt auf der Weltlinie des Elektrons bekommt so eine andere Eigenzeit zugeordnet. Anders ausgedrückt: Während die Eigenzeit $\tau$ auf der Uhr des Elektrons verstreicht, schreitet der entsprechende Raum-Zeit-Punkt $x$ auf der Weltlinie des Elektrons voran und zeigt so an, an welchem Ort $\mathit{x}$ sich das Elektron zu der entsprechenden Zeit $t$ des äußeren Beobachters aufhält.

Mathematisch bedeutet das, dass wir die Eigenzeit $\tau$ als Kurvenparameter der Weltlinie verwenden, sodass alle vier Raum-Zeit-Koordinaten von $x$ Funktionen von $\tau$ sind –wir schreiben deshalb auch $$x(\tau )$$ Wie schnell ändern sich die Raum- und Zeit-Koordinaten des Elektrons im Bezugssystem des äußeren Beobachters, wenn die Eigenzeit $\tau$ des Elektrons voranschreitet? Mathematisch entsprechen diese Änderungsraten den Ableitungen der vier Kordinaten nach der Eigenzeit. Wir fassen diese vier Ableitungen wieder zu einem vierkomponentigen Vektor zusammen und nennen ihn die Vierergeschwindigkeit $u$ des Elektrons (genau diese Vierergeschwindigkeit hatte Wheeler oben gemeint):

Vierergeschwindigkeit: $$u=\frac{dx}{d\tau }=\left(\begin{array}{c}c\frac{dt}{d\tau }\\ \frac{d\mathit{x}}{d\tau }\end{array}\right)=\left(\begin{array}{c}c\frac{dt}{d\tau }\\ \frac{d{x}^1}{d\tau }\\ \frac{d{x}^2}{d\tau }\\ \frac{d{x}^3}{d\tau }\end{array}\right)$$

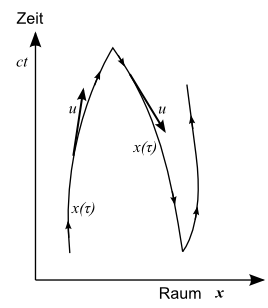
Damit haben wir schon fast alle Zutaten zusammen, um die Bewegung des Elektrons in einem äußeren elektromagnetischen Feld relativistisch zu beschreiben. Was noch fehlt ist ein geeignetes Objekt, das auch dieses elektromagnetische Feld umfasst.

Dazu bildet man aus den drei Komponenten des elektrischen Feldvektors $\mathit{E}$ und den drei Komponenten des magnetischen Feldvektors $\mathit{B}$ den sogenannten Feldstärketensor $F$, den man als 4-mal-4-Matrix mit insgesamt 16 Komponenten $F^{\mu \nu }$ darstellen kann. Die beiden Indizes $\mu$ und $\nu$ laufen dabei von 0 bis 3, so wie wir das oben auch bei den Komponenten des Vierervektors $x$ und der Vierergeschwindigkeit $u$ hatten.

Wie der Feldstärketensor mit den Komponenten des elektrischen und magnetischen Feldes zusammenhängt, kann man beispielsweise auf Wikipedia: Elektromagnetischer Feldstärketensor nachlesen:

elektromagnetischer Feldstärketensor: $$(F^{\mu \nu })=$$ $$=\left(\begin{array}{cccc}0& -E^1/c& -E^2/c& -E^3/c\\ E^1/c& 0& -B^3& B^2\\ E^2/c& B^3& 0& -B^1\\ E^3/c& -B^2& B^1& 0\end{array}\right)=$$ $$=:\left(\begin{array}{cc}0& -\mathit{E}/c\\ \mathit{E}/c& \mathcal{B}\end{array}\right)$$

Jetzt sind wir soweit, um die Bewegungsgleichung eines Elektrons mit Masse m und Ladung q in relativistischer Schreibweise darzustellen. Diese Bewegungsgleichung, die die Lorentzkraft auf das Elektron widerspiegelt, lautet:

kovariante Bewegungsgleichung: $$m\frac{d{u}^{\mu }}{d\tau }=q{F}^{\mu \nu }{u}_{\nu }$$

Dabei haben wir rechts die Indices der Vierergeschwindigkeit $u$ unten geschrieben. Das entspricht der üblichen Vorzeichenkonvention in der Relativitätstheorie: $$u_0=u^0$$ $$u_k=-u^k$$ mit $k=1,2,3$. Über doppelt vorkommende Indices wird summiert, d.h. rechts steht die Summe über $\nu$ von 0 bis 3.

Dass diese Bewegungsgleichung tatsächlich die bekannte Lorentzkraft in anderer Schreibweise darstellt, schauen wir uns unten noch genauer an. Die obige Schreibweise hat den Vorteil, dass sich die einzelnen Größen sehr einfach zwischen verschiedenen Beobachtern umrechnen lassen, was wir uns hier nicht genauer ansehen wollen. Das liegt daran, dass wir die Vierergeschwindigkeit und den 4-mal-4-Feldstärketensor als Basis für die Gleichung verwendet haben. Man bezeichnet eine solche Formulierungsweise auch als kovariant. Bei der gewohnten räumlichen Vektorschreibweise (siehe unten) ist die Umrechnung zwischen verschiedenen Beobachtern dagegen viel umständlicher.

Nun sind wir soweit, um Wheelers Überlegung zu Elektronen zu verstehen, die rückwärts in der Zeit reisen. Wiederholen wir noch einmal Feynmans Worte von oben, mit denen er diese Idee beschreibt:

"If in one section this is an ordinary electron world line, in the section in which it reversed itself and is coming back from the future we have the wrong sign to the proper time – to the proper four velocities – and that's equivalent to changing the sign of the charge, and, therefore, that part of a path would act like a positron."

In den Bereichen der Weltlinie, in denen sich das Elektron rückwärts durch die Zeit bewegt, sieht der äußere Beobachter die innere Uhr des Elektrons also rückwärts laufen, während auf seiner eigenen Uhr die Zeit vorwärts läuft. Die Eigenzeit (engl.: proper time) $\tau$ des Elektrons läuft dort also in umgekehrter Richtung wie die äußere Zeit $t$. Wenn $\tau$ wächst, schrumpft $t$ und umgekehrt. Damit haben wir präzise beschrieben, was es bedeuten soll, dass ein Elektron rückwärts durch die Zeit reist. Genau das ist oben mit dem Satz "we have the wrong sign to the proper time" gemeint.

Wenn ein Elektron rückwärts statt vorwärts in der Zeit reist, so wechselt auch die zugehörige Vierergeschwindigkeit $u$ die Richtung, denn die Vierergeschwindigkeit zeigt entlang der Weltlinie immer in die Richtung wachsender Eigenzeit (siehe Grafik oben). Das ist mit dem Zusatz "to the proper four velocities" gemeint.

Auf der rechten Seite der Bewegungsgleichung $$q{F}^{\mu \nu }{u}_{\nu }$$ wechselt also die Vierergeschwindigkeit $u$ das Vorzeichen, wenn das Elektron rückwärts statt vorwärts in der Zeit läuft: $$q{F}^{\mu \nu }(-u_{\nu })$$ Dieses Vorzeichen können wir wiederum zur Ladung ziehen: $$(-q)F^{\mu \nu }{u}_{\nu }$$ Statt die Vierergeschwindigkeit umzudrehen, können wir also auch das Vorzeichen der Ladung ändern. Ein Wechsel in der Zeitrichtung entspricht also einem Vorzeichenwechsel in der Ladung. Das ist oben mit dem Satz "and that's equivalent to changing the sign of the charge, and, therefore, that part of a path would act like a positron" gemeint.

Die linke Seite $$m\frac{d{u}^{\mu }}{d\tau }$$ der Bewegungsgleichung ändert übrigens nicht das Vorzeichen, wenn das Elektron rückwärts statt vorwärts in der Zeit reist, denn sowohl $u$ als auch $\tau$ wechseln das Vorzeichen, was sich gegenseitig aufhebt.

Falls Ihnen diese Argumentation noch etwas windig vorkommt, wollen wir sie noch etwas konkreter und mathematischer fassen. Dazu setzen wir $$u=\frac{dx(\tau )}{d\tau }$$ in die Bewegungsgleichung ein und erhalten: $$m\frac{d}{d\tau }\frac{d{x}^{\mu }(\tau )}{d\tau }=q{F}^{\mu \nu }\frac{d{x}_{\nu }(\tau )}{d\tau }$$ Wir nehmen nun an, dass diese Bewegungsgleichung die gesamte Weltlinie des Elektrons beschreibt, sowohl die Bereiche, in denen es in die Zukunft fliegt, als auch die Bereiche, in denen es in die Vergangenheit reist.

Schauen wir uns also einen Bereich der Weltlinie $x(\tau )$ an, in dem das Elektron in die Vergangenheit reist, sodass die Weltlinie dort mit wachsender Eigenzeit $\tau$ immer weiter rückwärts in der Zeit $t$ führt. Wie sieht dieses Elektron in der normalen Zeitrichtung $t$ aus?

Um das herauszufinden, ersetzen wir in der Bewegungsgleichung überall $\tau$ durch $-\tau$ und erhalten: $$m\frac{d}{-d\tau }\frac{d{x}^{\mu }(-\tau )}{-d\tau }=q{F}^{\mu \nu }\frac{d{x}_{\nu }(-\tau )}{-d\tau }$$ Die Vorzeichen von $-d\tau$ ziehen wir jeweils nach vorne, wobei sie sich links wegheben, rechts aber nicht, weshalb wir das Vorzeichen dort zur Ladung ziehen: $$m\frac{d}{d\tau }\frac{d{x}^{\mu }(-\tau )}{d\tau }=-q{F}^{\mu \nu }\frac{d{x}_{\nu }(-\tau )}{d\tau }$$ Nun schreiben wir noch $$y(\tau ):=x(-\tau )$$ Der Vierervektor $y(\tau )$ fährt in der Raumzeit mit wachsender Eigenzeit $\tau$ genau dieselbe Weltlinie ab wie der Vierervektor $x(\tau )$, nur in entgegengesetzter Richtung. Wir haben also die Richtung der Eigenzeit entlang der Weltlinie umgedreht. Wenn wir die Weltlinie also durch den Vierervektor $y(\tau )$ beschreiben, so wandert dieser Vektor dort vorwärts durch die Zeit, wo $x(\tau )$ rückwärts in der Zeit wandert. Einsetzen dieser neuen Weltlinien-Parametrisierung in die Bewegungsgleichung ergibt: $$m\frac{d}{d\tau }\frac{d{y}^{\mu }(\tau )}{d\tau }=-q{F}^{\mu \nu }\frac{d{y}_{\nu }(\tau )}{d\tau }$$ Diese Bewegungsgleichung entspricht einem Teilchen mit entgegengesetzter Ladung.

Ein Elektron, das rückwärts durch die Zeit reist, entspricht also einem Positron, das vorwärts durch die Zeit reist.

Man kann schnell in Verwirrung geraten, wenn man über Elektronen nachdenkt, die rückwärts in der Zeit reisen. Man könnte beispielsweise intuitiv zunächst vermutet, dass wir die Zeit dafür generell in umgekehrter Richtung ablaufen lassen müssen, die physikalische Bewegung des Elektrons also umkehren müssen. Das ist aber gar nicht gemeint!

Es geht vielmehr um folgendes: Die physikalische Bewegung des Teilchens (ob nun Elektron oder Positron) ist durch seine Weltlinie in der Raumzeit komplett festgelegt, denn diese Weltlinie sagt aus, wann der äußere Beobachter das Teilchen wo antrifft. Die Kurve, die das Teilchen in der Raumzeit beschreibt, ist also alles, was man braucht.

Man kann nun die Weltlinie auf verschiedene Weise parametrisieren. Dazu hatten wir einen Kurvenparameter $\tau$ eingeführt und ihn Eigenzeit genannt (warum das gerechtfertigt ist, kommt weiter unten). Natürlich würden wir normalerweise die Weltlinie in positiver Zeitrichtung durchlaufen, sodass eine wachsende Eigenzeit auch eine wachsende äußere Zeit bedeutet. Wir haben aber mathematisch die Freiheit, die Weltlinie auch in umgekehrter Richtung zu durchlaufen, also die Richtung der Eigenzeit umzudrehen. Dies entspricht einem Wechsel in der Parametrisierung der Weltlinie durch die Eigenzeit, wie wir es durch die Formel $y(\tau ):=x(-\tau )$ ausgedrückt haben.

Physikalisch ändert sich durch diese Umparametrisierung der Weltlinie die Bewegung des Teilchens nicht. Es ist ja immer noch dieselbe Weltlinie, d.h. das Teilchen befindet sich für den äußeren Beobachter immer noch zu den verschiedenen Zeitpunkten t an denselben Orten $\mathit{x}$.

Die Weltlinie hatten wir nun durch eine Differentialgleichung $$m\frac{d{u}^{\mu }}{d\tau }=q{F}^{\mu \nu }{u}_{\nu }$$ ausgedrückt, in die die Parametrisierung und damit die Eigenzeit eingeht.

Dabei haben wir festgestellt: Wenn wir die Richtung umdrehen, mit der wir die Weltlinie bei wachsender Eigenzeit durchlaufen, wenn wir also von der Parametrisierung $x(\tau )$ zur Parametrisierung $y(\tau ):=x(-\tau )$ wechseln, so erfüllt $y(\tau )$ nahezu dieselbe Differentialgleichung wie $x(\tau )$, nur mit umgedrehtem Ladungsvorzeichen.

Die Weltlinie eines Positrons, das der äußere Beobachter sieht, können wir in diesem Sinne auf zwei verschiedene Weisen interpretieren und durch die Differentialgleichung mathematisch beschreiben: Entweder wie üblich als Positron, dessen Eigenzeit bei wachsender äußerer Zeit anwächst, oder aber als Elektron, dessen Eigenzeit bei wachsender äußerer Zeit schrumpft und das sich in diesem Sinne rückwärts in der Zeit bewegt. In beiden Fällen ist es dieselbe Weltlinie und damit dieselbe physikalische Bewegung, nur die Interpretation und zugehörige mathematische Beschreibung durch die Differentialgleichung ist unterschiedlich.

Umformulierung in die dreidimensionalen Bewegungsgleichungen

Noch etwas deutlicher wird die Argumentation, wenn wir die kovariante Bewegungsgleichung $$m\frac{d{u}^{\mu }}{d\tau }=q{F}^{\mu \nu }{u}_{\nu }$$ in die gewohnte Schreibweise mit räumlichen Geschwindigkeiten und elektrischen und magnetischen Feldern übersetzen und dabei die Eigenzeit (bis auf ihr relatives Vorzeichen zur äußeren Zeit) eliminieren. Die Komponenten der Vierergeschwindigkeit schreiben wir dazu folgendermaßen um: $$u^0=\frac{d{x}^0}{d\tau }=c\frac{dt}{d\tau }$$ $$u^k=\frac{d{x}^k}{d\tau }=\frac{d{x}^k}{dt}\frac{dt}{d\tau }=v^k\frac{dt}{d\tau }$$ mit $k=1,2,3$ als Index für die drei räumlichen Komponenten und $$v^k:=\frac{d{x}^k}{dt}$$ für die Komponenten des normalen Geschwindigkeitsvektors $\mathit{v}$ des Teilchens im Bezugssystem des äußeren Beobachters. Zusammengefasst haben wir also $$u=\frac{dt}{d\tau }\cdot \left(\begin{array}{c}c\\ \mathit{v}\end{array}\right)$$ Der vierkomponentige Vektor $$\left(\begin{array}{c}c\\ \mathit{v}\end{array}\right)$$ hängt dabei nur von der Gestalt der Weltlinie in der Raumzeit ab, nicht aber von ihrer genauen Parametrisierung, denn der Vektor ist alleine dadurch festgelegt, zu welchen Zeiten $t$ der äußere Beobachter das Teilchen an welchen Orten $\mathit{x}$ sieht. Die Parametrisierung der Weltlinie spiegelt sich nur noch im Vorfaktor $$\frac{dt}{d\tau }$$ wider.

Man sieht hier sehr schön, dass die Vierergeschwindigkeit $u$ das Vorzeichen wechselt, wenn $dt/d\tau$ das Vorzeichen wechselt. Dieser Term $dt/d\tau$ ist positiv, wenn Eigenzeit $\tau$ und äußere Zeit $t$ gleich gerichtet sind, und er ist negativ, wenn eine wachsende Eigenzeit $\tau$ mit einer schrumpfenden äußeren Zeit $t$ einhergeht.

Wir wollen den Term $dt/d\tau$ noch etwas umschreiben, sodass die Eigenzeit $\tau$ daraus verschwindet (bis auf das relative Vorzeichen zwischen $dt$ und $d\tau$). Dazu müssen wir eine Bedingung an die Parametrisierung der Weltlinie stellen, die erst dazu führt, dass wir $\tau$ als Eigenzeit interpretieren können.

Wir fordern: Wenn das Teilchen im Bezugssystem des äußeren Beobachters ruht und demnach die Geschwindigkeit $\mathit{v}=0$ ist, dann soll $$dt=\pm d\tau$$ sein, d.h. die Eigenzeit läuft bei einem ruhenden Teilchen in genauso großen Schritten wie die äußere Zeit, wobei beide Zeiten aber auch gegenläufig verstreichen können (in diesem Fall gilt das Minuszeichen).

Anders ausgedrückt: Wenn $\mathit{v}=0$ ist, dann soll $dt/d\tau =\pm 1$ sein. Eine relativ zum Beobachter ruhende Uhr läuft genauso schnell wie die Uhr des Beobachters (ggf. bis auf das negative Vorzeichen, das wir hier im Sinne "bewegt sich rückwärts in der Zeit" interpretieren).

Was folgt daraus für $dt/d\tau$ bei anderen Geschwindigkeiten $\mathit{v}$?

Hier hilft eine Erkenntnis aus der Relativitätstheorie weiter, die folgendes besagt: Wenn man von einem unbeschleunigten Beobachter zu einem anderen unbeschleunigten Beobachter wechselt, so ändert sich im allgemeinen zwar die Vierergeschwindigkeit $$u=\left(\begin{array}{c}{u}^0\\ \mathit{u}\end{array}\right)$$ und damit auch die normale Geschwindigkeit $\mathit{v}$ des Teilchens, die der Beobachter wahrnimmt – die beiden Beobachter können sich ja geradlinig-gleichförmig gegeneinander bewegen. Was für den einen Beobachter ein ruhendes Teilchen ist, kann für den anderen Beobachter ein Teilchen sein, das sich mit der Geschwindigkeit $\mathit{v}$ bewegt.

Es gibt jedoch eine Größe, die für alle unbeschleunigten Beobachter immer gleich groß ist: Die Differenz aus dem Quadrat der Null-Komponente $u^0$ der Vierergeschwindigkeit minus dem Längenquadrat des räumlichen Vektors $\mathit{u}$, also die Größe $$(u^0{)}^2-{\mathit{u}}^2=$$ $$={\left(\frac{dt}{d\tau }\right)}^2\cdot (c^2-{\mathit{v}}^2)=$$ $$=\mathrm{k}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$ Warum das so ist, wollen wir hier nicht genauer begründen. Immerhin sieht man, dass wenn man für Licht in der Formel ${\mathit{v}}^2=c^2$ einsetzt, die obige Größe gleich Null ist. Da dies für alle unbeschleunigten Beobachter gelten soll, ist Licht für jeden dieser Beobachter gleich schnell, egal wie schnell sich die Beobachter relativ zueinander bewegen. Licht fliegt immer mit Lichtgeschwindigkeit, egal wer sich das Licht ansieht. Das ist eine der zentralen Aussagen der Speziellen Relativitätstheorie.

Für einen Beobachter, der ein ruhendes Teilchen sieht, ist $\mathit{v}=0$ und er erhält für die obige Größe den Wert $${\left(\frac{dt}{d\tau }\right)}^2\cdot c^2$$ Oben hatten wir für die Eigenzeit bereits gefordert: Wenn $\mathit{v}=0$ ist, dann soll $dt/d\tau =\pm 1$ sein und somit $(dt/d\tau {)}^2=1$. Die obige Größe ist also gleich $c^2$ für diesen Beobachter – und damit für alle Beobachter, denn jeder Beobachter erhält ja dasselbe Ergebnis für die obige Größe. Es gilt also allgemein für jeden Beobachter und damit für alle Geschwindigkeiten $$(u^0{)}^2-{\mathit{u}}^2=$$ $$={\left(\frac{dt}{d\tau }\right)}^2\cdot (c^2-{\mathit{v}}^2)=$$ $$=c^2$$ Das können wir nach $(dt/d\tau {)}^2$ freistellen und erhalten $${\left(\frac{dt}{d\tau }\right)}^2=\frac{c^2}{c^2-{\mathit{v}}^2}=$$ $$=\frac{1}{1-(\mathit{v}/c{)}^2}=:{\gamma }^2$$ mit dem positiven Lorentzfaktor

Lorentzfaktor: $$\gamma =\frac{1}{\sqrt{1-(\mathit{v}/c{)}^2}}$$

Insgesamt haben wir also für den Zusammenhang zwischen den (infinitesimalen) Zeitintervallen der äußeren Zeit und der Eigenzeit den folgenden Zusammenhang:

äußere Zeit und Eigenzeit: $$\frac{dt}{d\tau }=\pm \gamma$$ oder anders ausgedrückt $$dt=\pm \gamma d\tau$$

Der Lorentzfaktor $\gamma$ spiegelt dabei die sogenannte Zeitdilatation eines bewegten Objekts wider: Bei einem bewegten Objekt verstreicht dessen Eigenzeit langsamer als die äußere Zeit, da dann $\gamma$ größer als Eins ist.

Oder kurz: eine bewegte Uhr läuft für den äußeren Beobachtes langsamer als dessen eigene Uhr. Das kann man durchaus messen und es spiegelt sich auch beispielsweise in der Lebensdauer instabiler Teilchen wider: Ein schnelles Myon zerfällt im Mittel langsamer als ein ruhendes Myon.

Was man nicht messen kann, ist die Richtung der Eigenzeit relativ zur äußeren Zeit, also das Vorzeichen $\pm$ in der obigen Gleichung. Die Richtung der Zeit hat nämlich nur für makroskopische Objekte eine physikalische Bedeutung und spiegelt den Anstieg der Entropie wider. Für ein einzelnes Elektron können wir dagegen willkürlich wählen, ob seine Eigenzeit mit oder gegen die äußere Zeit anwachsen soll − genau das steckt hinter Wheelers Idee. Wir müssen uns dann nur fragen, was das physikalisch bedeutet, insbesondere welche Ladung der äußere Beobachter wahrnimmt.

Mit $dt/d\tau =\pm \gamma$ können wir die Vierergeschwindigkeit $$u=\frac{dt}{d\tau }\cdot \left(\begin{array}{c}c\\ \mathit{v}\end{array}\right)$$ nun scheiben als

Vierergeschwindigkeit: $$u=\pm \gamma \cdot \left(\begin{array}{c}c\\ \mathit{v}\end{array}\right)$$

Bis auf das relative Vorzeichen bezüglich der Richtung zwischen Eigenzeit und äußerer Zeit kommt die Eigenzeit hier gar nicht mehr vor. Das ist genau das, was wir brauchen, um die relativistische Bewegungsgleichung der Weltlinie in die gewohnte Form ohne Eigenzeit umzuformen. Wir starten also mit unserer Bewegungsgleichung $$m\frac{d{u}^{\mu }}{d\tau }=q{F}^{\mu \nu }{u}_{\nu }$$ die für die gesamte Weltlinie gelten soll, egal wie Eigenzeit und äußere Zeit zueinander orientiert sind. Das entspricht wieder der Grundidee, dass die Richtung der Eigenzeit relativ zur äußeren Zeit nicht festgelegt ist.

Eigentlich ist diese Bewegungsgleichung eine Ansammlung von vier Gleichungen – eine für jeden Wert von $\mu =0,1,2,3$.

Die Gleichung für $\mu =0$ und $\mu =k=1,2,3$ schreiben wir separat und ziehen analog auch die Summe rechts von $\nu =0$ bis $3$ auseinander in den Summanden mit $\nu =0$ und in eine Restsumme über $\nu =l$ von 1 bis 3: $$m\frac{d{u}^0}{d\tau }=q{F}^{00}{u}_0+q{F}^{0l}{u}_l$$ $$m\frac{d{u}^k}{d\tau }=q{F}^{k0}{u}_0+q{F}^{kl}{u}_l$$ Rechts wird hier also über $l$ von 1 bis 3 summiert.

Nun können wir $$u=\pm \gamma \cdot \left(\begin{array}{c}c\\ \mathit{v}\end{array}\right)$$ einsetzen, also $$u^0=\pm \gamma c=u_0$$ $$u^k=\pm \gamma v^k=-u_k$$ (analog für $l$ statt $k$). $$\pm m\frac{d(\gamma c)}{d\tau }=\pm q{F}^{00}\gamma c\pm q{F}^{0l}(-\gamma v^l)$$ $$\pm m\frac{d(\gamma v^k)}{d\tau }=\pm q{F}^{k0}\gamma c\pm q{F}^{kl}(-\gamma v^l)$$ Das Vorzeichen $\pm$ links und rechts hebt sich gegenseitig weg. Wir setzen außerdem $$F^{00}=0$$ $$F^{0l}=-E^l/c$$ $$F^{k0}=E^k/c$$ ein: $$m\frac{d(\gamma c)}{d\tau }=q{E}^l\gamma v^l/c$$ $$m\frac{d(\gamma v^k)}{d\tau }=q{E}^k\gamma -q{F}^{kl}\gamma v^l$$ In der ersten Gleichung ist die Summe über $l$ von $E^l{v}^l$ gleich dem Skalarprodukt der Vektoren $\mathit{E}$ und $\mathit{v}$, also gleich $\mathit{E}\mathit{v}$. Außerdem multiplizieren wir in der ersten Gleichung beide Seiten noch mit c.
Wir dividieren bei beiden Gleichungen beide Seiten noch durch $\gamma$ und verwenden auf der linken Seite im Nenner, dass $\gamma d\tau =\pm dt$ ist: $$\pm \frac{d(m\gamma c^2)}{dt}=q\mathit{E}\mathit{v}$$ $$\pm \frac{d(m\gamma v^k)}{dt}=q{E}^k-q{F}^{kl}{v}^l$$ Die Summe $F^{kl}{v}^l$ über $l$ in der zweiten Gleichung wollen wir als Beispiel für $k=1$ ausrechnen: $$F^{1l}{v}^l=$$ $$=F^{11}{v}^1+F^{12}{v}^2+F^{13}{v}^3=$$ $$0+(-B^3)v^2+B^2{v}^3=$$ $$-(\mathit{v}\times \mathit{B}{)}^1$$ also die erste Komponente des Vektor-Kreuzproduktes $-(\mathit{v}\times \mathit{B})$. Analog ist es auch bei den anderen Komponenten.

Wenn wir in beiden Gleichungen noch das Vorzeichen $\pm$ auf die andere Seite ziehen, und die drei Gleichungen für $k=1$ bis $3$ vektoriell zusammenfassen, erhalten wir schließlich:

Energieerhaltung und Bewegungsgleichung: $$\frac{d(m\gamma c^2)}{dt}=\pm q\mathit{E}\mathit{v}$$ $$\frac{d(m\gamma \mathit{v})}{dt}=\pm q(\mathit{E}+\mathit{v}\times \mathit{B})$$

Das sind genau die Bewegungsgleichungen für ein relativistisches Teilchen der Ladung $\pm q$ im elektrischen Feld $\mathit{E}$ und magnetischen Feld $\mathit{B}$ im Bezugssystems des äußeren Beobachters, wobei die obere Gleichung die Energieänderung des Teilchens aufgrund der Beschleunigung im elektrischen Feld repräsentiert.

Das Vorzeichen $\pm$ gibt dabei an, ob wir in der Weltlinie die Eigenzeit in oder gegen die äußere Zeit anwachsen lassen: $\gamma d\tau =\pm dt$. Lassen wir das Elektron also in der Weltlinie mit wachsender Eigenzeit $\tau$ in die Vergangenheit (also in die negative $t$-Richtung) reisen, so sieht der äußere Beobachter ein Positron in die positive $t$-Richtung reisen (die Eigenzeit des Elektrons kann er ja sowieso nicht sehen).