
Quelle: Wikimedia Commons File:Rudolf Clausius 01.jpg, dort public domain; Fotograf: Theo Schafgans, Zeitschrift für Physikalische Chemie, Band 21, von 1896
Wie effizient ist die beste Wärmekraftmaschine?
Die klassische Definition von Entropie und absoluter Temperatur
Die mikroskopische Interpretation der Entropie
Die Entropie gehört zu denjenigen physikalischen Größen, die
anders als beispielsweise die Energie wenig greifbar erscheinen.
Etwas Geheimnisvolles umgibt diesen Begriff, der wie durch Zauberei
bei der Betrachtung idealer Wärmekraftmaschinen ins Spiel kommt.
Aber auch die Temperatur, für die wir ein unmittelbares körperliches Empfinden
haben, ist keineswegs ein so einfacher Begriff, wie man zunächst glauben möchte.
Was genau sind also Entropie und Temperatur?
Die Geschichte des Entropiebegriffs begann mit dem Siegeszug der industriellen Revolution, speziell mit der Erfindung der Dampfmaschine um das Jahr 1700 herum. Mit solchen Wärmekraftmaschinen war es möglich geworden, die in Kohle und anderen brennbaren Stoffen gespeicherte Energie über die Erzeugung von Wärme (Verbrennung) in mechanische Arbeit umzuwandeln, und bald stellte sich die Frage, wie Arbeit, Energie und Wärme physikalisch zusammenhängen und wie weit man die Effizienz solcher Maschinen steigern kann.
Den Zusammenhang von Wärme und Energie haben wir uns bereits im Kapitel Was ist Energie? angesehen. Dabei sind wir auf den ersten Hauptsatz der Thermodynamik gestoßen, den man erst um das Jahr 1840 herum klar herausgearbeitet hatte. Er sagt, dass sich die innere Energie \( U \) eines Körpers auf zwei Weisen ändern kann: entweder durch Änderung äußerer Parameter wie beispielsweise dem Volumen, wobei eine gewisse Arbeit \( \delta W \) am Körper geleistet wird, oder durch einen mikroskopischen Energiefluss bei konstanten äußeren Parametern, durch den eine gewisse Wärmemenge \( \delta Q \) in den Körper hineinfließt (oder ihn bei negativem Vorzeichen verlässt):
\begin{equation} dU = \delta Q + \delta W \end{equation}
Die innere Energie \( U \) war dabei eingeführt worden, um den Energieerhaltungssatz sicherzustellen. Sie entspricht der kinetischen plus potentiellen Energie der mikroskopischen Teilchen, die den Körper aufbauen, und sie ist eine Zustandsgröße, denn man kann immer sagen, welche innere Energie \( U \) ein Körper besitzt. Bei der Wärmemenge \( \delta Q \) und der Arbeit \( \delta W \) ist das anders: Sie sind Prozessgrößen und verknüpfen eine Energieänderung mit einem zugehörigen Prozess, nämlich mit oder ohne Änderung äußerer Parameter wie dem Volumen. Sie sind aber keine Zustandsgrößen, d.h. man kann nicht sagen, dass ein Körper eine bestimmte Wärmemenge oder Arbeitsmenge besitzt – daher die unterschiedliche Schreibweise \( d \) bzw. \( \delta \) in der Formel oben.
Die obige Formulierung gilt für infinitesimal kleine Energieänderungen \( dU \), aber man kann sie genauso gut für größere Änderungen \( \Delta U \) formulieren: \begin{equation} \Delta U = Q + W \end{equation} Damit ist im Prinzip klar, was eine Dampfmaschine macht: Sie wandelt eine Wärmemenge \( Q \), die man beispielsweise durch das Verbrennen von Kohle dem Arbeitsmedium Wasserdampf zuführt, ganz oder teilweise in mechanische Arbeit \( Q \) um, die dieser Dampf dann leistet. Wie effizient dies geschieht, darüber macht der erste Hauptsatz keine Aussage, denn dafür müssen wir genauer verstehen, was eine Wärmemenge \( Q \) eigentlich zum Fließen bringt.
Warum Arbeit die innere Energie eines Körpers ändern kann, ist anschaulich klar: Wenn man beispielsweise bei einem Gas das Gasvolumen verkleinert, so muss man gegen den Gasdruck arbeiten und erhöht dabei die Bewegungsenergie der einzelnen Gasteilchen. Umgekehrt kann sich die Energie des Gases auch verringern, wenn man das Gasvolumen vergrößert, so wie das bei einem Zylinderkolben in einer Dampfmaschine der Fall ist: Der Dampf expandiert und treibt den Kolben nach außen, wodurch Arbeit an einem äußeren Objekt verrichtet werden kann (W ist bei der Vorzeichenkonvention in der Formel oben dann negativ).
Doch was sorgt dafür, dass eine Wärmemenge \( Q \) in einen Körper hineinfließt oder diesen verlässt, ohne dass sich beispielsweise das Volumen ändert? Aus Erfahrung wissen wir, dass die Temperatur hier die treibende Kraft ist: Wärme fließt von selbst (also ohne dass sonstige Änderungen zusätzlich vorgenommen werden) immer von einem wärmeren zu einem kälteren Körper hin, niemals aber umgekehrt. Der deutsche Physiker Rudolf Clausius hat diesen sogenannten zweiten Hauptsatz der Therodynamik um 1850 auch so formuliert:

Quelle:
Wikimedia Commons File:Rudolf Clausius 01.jpg, dort public domain;
Fotograf: Theo Schafgans, Zeitschrift für Physikalische Chemie, Band 21, von 1896
Natürlich ist es sehr wohl möglich, Wärme von einem kälteren auf einen wärmeren Körper zu übertragen – ein Kühlschrank tut genau das! Er tut aber noch mehr, denn er benötigt zusätzlich die Zufuhr von elektrischer Energie (Arbeit). Daher ist das Wort "einziges" in der obigen Formulierung sehr wichtig, was gleichbedeutend damit ist, dass die Wärme nicht von selbst von kalt nach warm fließt.
Die obige harmlos aussehende Formulierung des zweiten Hauptsatzes enthält bereits alles, was wir in der folgenden Diskussion brauchen. Weiter unten werden wir noch andere gleichwertige Formulierungen kennenlernen. In der obigen Formulierung taucht zum ersten Mal der Begriff der Temperatur auf, der im ersten Hauptsatz noch gar nicht benötigt wird. Doch was genau ist Temperatur eigentlich?
Bei einem (idealen) Gas können wir die Temperatur \( T \) beispielsweise als die mittlere
kinetische Energie \( E_\mathrm{kin} \) der einzelnen Gasmoleküle definieren, wobei die Gasmoleküle
sich ansonsten vollkommen zufällig im Gas bewegen. Mit einem passenden Vorfaktor
(der sogenannten Boltzmannkonstante \( k \) sowie einem weiteren Vorfaktor 3/2)
können wir diese Definition auch
an die übliche Kelvin-Skala anpassen:
\begin{equation}
E_\mathrm{kin} = \frac{3}{2} k T
\end{equation}
Quelle:
Wikimedia Commons File:Translational motion.gif,
von A.Greg,
Creative Commons Attribution-Share Alike 3.0 Unported license
Aus dieser Temperaturdefinition kann man beispielsweise die allgemeine Gasgleichung herleiten, die den Zusammenhang zwischen Druck, Volumen und Temperatur einer bestimmten Gasmenge angibt, und damit ein Gasthermometer bauen, mit dem sich Temperaturen messen lassen.
Ausgehend von dieser mikroskopischen Interpretation der Temperatur können wir leicht sagen, was beim Wärmetransport geschieht: Im wärmeren Gas haben die Gasmoleküle im Durchschnitt eine höhere Bewegungsenergie als im kühleren Gas. Der Wärmetransport erfolgt nun durch zufällige Stöße zwischen den Gasmolekülen (z.B. vermittelt über eine thermisch leitende Trennwand), bis sich die statistisch wahrscheinlichste Energieverteilung herausgebildet hat, bei der beide Gasanteile dieselbe Temperatur haben. Die kinetische Energie verteilt sich dabei zufällig auf alle Gasmoleküle, wobei sie im Mittel für alle Gasmoleküle gleich groß ist. Der zweite Hauptsatz hat also etwas mit Wahrscheinlichkeiten zu tun. Wir sollten dieses Bild im Gedächtnis behalten, denn wir werden weiter unten wieder darauf zurückkommen.
Welche Voraussetzungen brauchen wir nun, damit eine zyklisch arbeitende Wärmekraftmaschine eine Wärmemenge \( Q \) in Arbeit \( W \) umwandeln kann? Nun, am einfachsten und effektivsten wäre eine Maschine, die ohne jede Energiezufuhr von außen nichts anderes macht, als einen Wasserbehälter abzukühlen und die entnommene innere Energiemenge \( \Delta U \) des Wassers komplett als Arbeit \( W \) nutzbar zu machen. Insbesondere soll dabei nach einem Arbeitszyklus alles innerhalb der Maschine wieder genauso aussehen wie vorher, und die Maschine soll auch selbst keinerlei Wärme abgeben, d.h. die Umwandlung der entnommenen Wärme in Arbeit soll vollständig sein. Geht so etwas? Gibt es ein solches Perpetuum Mobile zweiter Art, wie man eine solche Maschine auch nennt?
Leider nein, denn wenn wir mit dieser gewonnenen Arbeit beispielsweise über Reibung einen zweiten wärmeren Wasserbehälter weiter aufwärmen, dann macht die Maschine insgesamt nichts anderes, als Wärme von einem kälteren zu einem wärmeren Medium zu transportieren, ohne sonst irgendetwas zu tun oder zu benötigen. Eine solche Maschine kann es aber nicht geben, wie uns der zweite Hauptsatz sagt! Man bräuchte schon eine Energiezufuhr von außen, um eine solche Maschine zu bauen – eine Wärmepumpe wäre eine solche Maschine!
Wie sähe die Lage dagegen aus, wenn wir von vorne herein zwei Wasserbehälter
mit unterschiedlichen Temperaturen zur Verfügung hätten,
sodass die Maschine nicht nur dem heißeren Wasserbehälter Wärme entnehmen kann,
sondern auch Wärme an den kälteren Wasserbehälter abgeben kann?
Ist dann die Entnahme einer Wärmemenge aus dem heißeren Behälter mit teilweiser Umwandlung in Arbeit möglich?
Genau darüber hatte sich bereits im Jahr 1824 der französischen Offizier und Ingenieur Nicolas Léonard Sadi Carnot
Gedanken gemacht – das war knapp 20 Jahre vor der Entdeckung
des ersten Hauptsatzes (Energieerhaltung), den Carnot noch nicht kannte.

Quelle:
Wikimedia Commons File:Sadi Carnot.jpeg, dort public domain.
Zur Vereinfachung wollen wir ab sofort annehmen, dass die beiden Wasserbehälter auch bei Zufuhr oder Entnahme von Wärmemengen ihre Temperatur beibehalten – sie könnten beispielsweise einfach sehr groß sein, oder aber durch sonstige Maßnahmen (z.B. das Verbrennen von Kohle bzw. das Kühlen mit Kühlwasser) auf konstanter Temperatur gehalten werden. Das kommt einer Dampfmaschine schon recht nahe.
Carnot stellte sich nun vor, dass ein unzerstörbarer Wärmestoff vom heißeren zum kälteren Behälter fließt und dabei Arbeit verrichtet, genauso wie Wasser Arbeit verrichtet, wenn es ein Gefälle herabfließt. Die Temperaturdifferenz der Wasserbehälter sollte dabei wie ein Höhenunterschied wirken. Zwanzig Jahre später war mit der Entdeckung des ersten Hauptsatzes klar, dass es diesen unzerstörbaren Wärmestoff nicht gibt und dass sich ein Teil der fließenden Wärme in Arbeit umwandelt. Dennoch erwiesen sich viele Überlegungen Carnot's als richtig, denn es gibt eine andere Größe, die dieses Temperaturgefälle gewissermaßen herunterfließt und die im Grenzfall einer maximal effektiven (reversiblen) Maschine erhalten bleibt: die Entropie. Dieser Begriff wurde allerdings erst im Jahr 1865, also rund 30 Jahre nach Carnot's Tod, von Rudolf Clausius eingeführt – dieser große Physiker ist uns oben beim zweiten Hauptsatz bereits begegnet.
Schauen wir uns an einem konkreten Beispiel an, wie diese geheimnisvolle Entropie zustande kommt. Dazu betrachten wir als möglichst einfache Wärmekraftmaschine einen Gas-gefüllten Zylinder mit einem Kolben, mit dem man das Gasvolumen im Zylinder verändern kann. Das Gas soll ein ideales Gas sein. Es dient als Arbeitsmedium, das man mit dem Kolben im Zylinder zusammendrücken kann und das den Kolben auch wieder nach außen drücken kann. Über die Kolbenbewegung kann das Gas dabei Arbeit verrichten. Den Zylinder können wir nach Belieben mit dem heißen oder dem kalten Wasserbehälter in Kontakt bringen und dadurch das Gas aufheizen oder abkühlen.
Wir wollen dabei in idealisierter Form voraussetzen, dass jede Form von Reibung ausgeschlossen ist, d.h. der Kolben im Gaszylinder soll sich völlig reibungsfrei bewegen. Außerdem soll es keinerlei innere Reibung im Gas geben, also keine Strömungen oder gar Turbulenzen. Das erreichen wir, indem wir nur sehr langsame Bewegungen des Kolbens zulassen und jeden Aufheizungs- und Abkühlvorgang durch Kontakt mit einem der beiden Wasserbehälter ganz langsam und vorsichtig vornehmen. Die Wärme soll also nur durch minimale Temperaturunterschiede vom Wasserbehälter ins Gas oder umgekehrt fließen – Gas und Wasserbehälter müssen also beim Wärmefluss fast dieselbe Temperatur aufweisen.
Eine ideale Wärmekraftmaschine arbeitet also letztlich unendlich langsam und mit nur infinitesimalen Temperaturunterschieden bei Wärmeflüssen – was natürlich ein Gedankenexperiment ist, denn mit jeder realen Maschine lässt sich eine solche ideale Maschine nur angenähert realisiseren. Die ideale Maschine arbeitet sogar reversibel in dem Sinne, dass wir durch Umkehr der infinitesimalen Temperaturunterschiede und Umkehr der unendlich langsamen Bewegung alle Vorgänge rückwärts ablaufen lassen können. Für eine ideale Maschine gibt es also letztlich keine Zeitrichtung und – wegen dem unendlich langsamen Ablauf – auch keine Zeit. Eine reale Wärmekraftmaschine wird daher niemals ideal sein – höchstens nahezu ideal.
Schauen wir uns also nun unter diesen Randbedingungen unseren Gaszylinder an, den wir Carnot-Maschine nennen wollen. Ein Arbeitszyklus dieser Carnot-Maschine soll nun folgendermaßen aussehen (Carnot-Kreisprozess) :
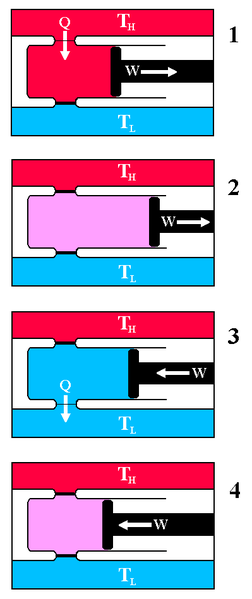
Quelle:
Wikimedia Commons File:Carno engine.PNG, dort public domain.
In den ersten beiden Schritten verrichtet das expandierende Gas Arbeit, da der Kolben nach außen gedrückt wird und sich das Gasvolumen vergrößert. Dabei wird im ersten Schritt die komplette aufgenommene Wärmemenge \( Q_1 \) in Arbeit umgewandelt, denn wegen der konstanten Temperatur des Gases bleibt auch die kinetische Energie der Gasteilchen konstant, sodass sich die innere Energie \( U \) des Gases nicht ändert. Die im zweiten Schritt verrichtete Arbeit speist sich dagegen komplett aus der inneren Energie \( U \) des Gases, da keinerlei Wärme mehr zugeführt wird.
Es ist also mit Schritt 1 sehr wohl möglich, Wärme komplett in Arbeit umzuwandeln, wobei sich allerdings der Zustand des Gases verändert. Das ist kein Widerspruch zum zweiten Hauptsatz, denn verboten ist nur eine Maschine, die nichts anderes macht, als einen Körper abzukühlen und die entnommene Wärme komplett in Arbeit umzuwandeln. Mit nichts anderes ist gemeint, dass sich auch der innere Zustand der Maschine dabei nicht ändern darf, wenn ein Umwandlungszyklus abgeschlossen ist. Das ist genau der Grund dafür, warum wir die Schritte 2 bis 4 brauchen: Sie stellen den ursprünglichen Zustand der Maschine wieder her!
Im dritten und vierten Schritt muss dabei Arbeit aufgewendet werden, um den Kolben gegen den Gasdruck langsam wieder bis zu seiner Ursprungsposition in den Gaszylinder hineinzudrücken. Dabei wird in Schritt 3 – umgekehrt zu Schritt 1 – die am Gas verrichtete Arbeit komplett in Wärme umgewandelt und als Wärmemenge \( Q_2 \) an den kälteren Wasserbehälter abgegeben. In Schritt 4 geht die zugeführte Arbeit dagegen in die innere Energie \( U \) des Gases über, sodass am Schluss wieder der Ausgangszustand hergestellt ist. Dabei wird in Schritt 4 genau dieselbe Arbeit zugeführt, die in Schritt 2 gewonnen wurde, denn die Schritte 2 und 4 ändern die innere Energie \( U \) des Gases in genau entgegengesetzter Weise, um zwischen den Temperaturniveaus der beiden Wasserbehälter hin- und herzuwechseln.
Da die Temperatur im ersten Schritt aber größer als im dritten Schritt ist,
findet die Expansion in Schritt 1 bei durchschnittlich höherem Druck statt als
die Kompression im dritten Schritt, sodass das Gas in Summe Arbeit nach außen leistet.
Mathematisch ausgesrückt ist die Arbeit gleich dem Integral von
\( dW = p \, dV \)
über einen Zyklus
und entspricht damit der umlaufenen Fläche in folgendem p-V-Diagramm:
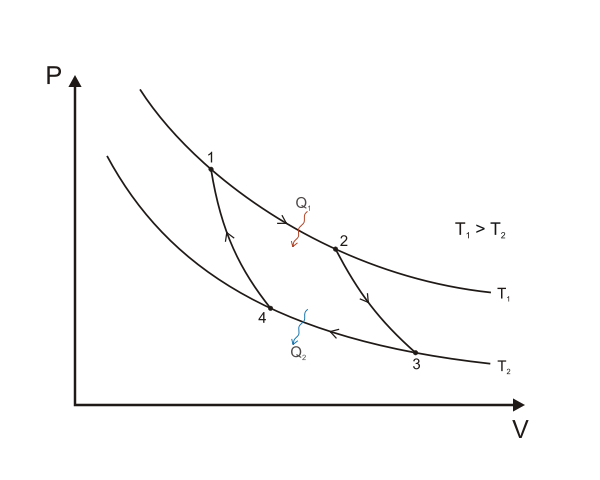
Quelle:
Wikimedia Commons File:Carnot cycle p-V diagram.svg von Keta,
Creative Commons Attribution-Share Alike 3.0 Unported license.
Aufgrund der Energieerhaltung (erster Hauptsatz) muss die pro Zyklus nach außen geleistete Gesamtarbeit aus der Differenz der Wärmemengen \( Q_1 \) und \( Q_2 \) stammen, die bei hoher Temperatur \( T_1 \) vom Gas aufgenommen und bei niedriger Temperatur \( T_2 \) an das kalte Wasser abgegeben wurde: \begin{equation} W = Q_1 - Q_2 \end{equation} Dabei treffen wir die Konvention, dass alle drei Größen positiv sind, wenn wir sie im obigen Sinne interpretieren: \( Q_1 \) wird vom Gas im Kolben aufgenommen, \( Q_2 \) und \( W \) werden vom Gas abgegeben.
Bleibt die Frage, wie groß die aufgenommene bzw. abgegebene Wärmemenge und damit die Arbeitsausbeute ist. Rechnet man den Zyklus mithilfe der idealen Gasgleichung durch, so stößt man auf folgende zentrale Beziehung (die Rechnung findet man beispielsweise in Wikipedia: Carnot-Prozess sowie in Feynman Lectures of Physics I, 44 The Laws of Thermodynamics): \begin{equation} \frac{Q_1}{T_1} = \frac{Q_2}{T_2} \end{equation} oder anders geschrieben \begin{equation} \frac{Q_1}{Q_2} = \frac{T_1}{T_2} \end{equation}
Auch ohne konkrete Rechnung kann man sich folgendermaßen vorstellen, wie diese
entscheidende Beziehung zwischen Wärmemengen und Temperaturen zustande kommt:
Eine reversible Maschine macht nämlich nur den Energieunterschied der Teilchen in den beiden
Wärmereservoiren als Arbeit nutzbar, nicht aber die gesamte Energie, die sie tragen.
Könnte die Maschine die gesamte Energie, die \(N\) Teilchen bei der heißeren
Temperatur \( T_1 \) besitzen, als Wärmemenge
\( Q_1 = N \, (3/2) \, k T_1 \) entnehmen, so müsste sie ihnen mindestens die Wärmemenge
\( Q_2 = N \, (3/2) \, k T_2 \) zurückgeben, damit sie nicht kälter als \( T_2 \) werden
(wir verwenden hier vereinfacht die Formeln für ein ideales Gas).
Der Grund für dieses Verhalten liegt darin, dass die Maschine die \(N\) Teilchen nicht stärker abkühlen kann als
bis zur Temperatur \( T_2 \), denn es gibt kein kälteres Medium, das in Kontakt mit
der Maschine stünde. Diese thermische Restenergie der Teilchen lässt sich also nicht weiter nutzen,
denn dazu bräuchte man ein noch kälteres Kühlmedium. Also ist
\begin{equation}
\frac{Q_1}{Q_2} = \frac{N \, (3/2) \, k T_1}{N \, (3/2) \, k T_2} = \frac{T_1}{T_2}
\end{equation}
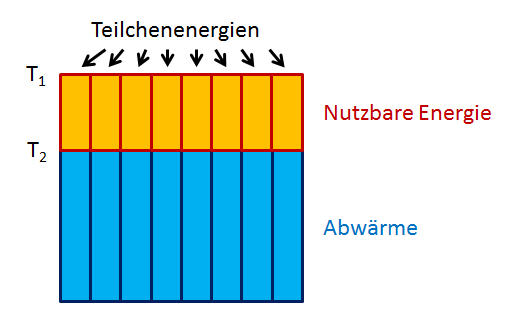
Wie effektiv ist also nun die Umwandlung von Wärme in Arbeit bei einem gegebenen Temperaturunterschied zweier großer Wasserbehälter? Wie hoch ist der Wirkungsgrad \( \eta \), also der Anteil an Arbeit \(W\), den wir von der aufgenommenen Wärmemenge \( Q_1 \) abzweigen können? Rechnen wir es aus: \begin{align} \eta &= \frac{W}{Q_1} = \frac{Q_1 - Q_2}{Q_1} = \\ & \\ &= 1 - \frac{Q_2}{Q_1} = 1 - \frac{T_2}{T_1} = \\ & \\ &= \frac{T_1 - T_2}{T_1} \end{align} d.h. je größer der Temperaturunterschied der Wasserbehälter ist, umso größer ist auch der Wirkungsgrad unserer Carnot-Wärmekraftmaschine. Größer als 1 wird er jedoch nie, und 1 erreicht er auch nur dann, wenn die Temperatur \( T_2 \) des kühlenden Wassertanks gegen Null geht, sodass auch keine Abwärme \( Q_2 \) mehr anfällt. Ist dagegen der Temperaturunterschied gleich Null, so kann überhaupt keine Arbeit mehr gewonnen werden – ganz im Einklang mit dem zweiten Hauptsatz.
Nun ist die obige Carnot-Maschine mit ihrem Gaszylinder und dem speziellen Carnot-Zyklus natürlich eine ganz spezielle reversible Maschine. Kann man mit einer anderen Maschine – reversibel oder nicht – einen noch höheren Wirkungsgrad erreichen?
Naja – immerhin arbeitet unsere idealisierte Carnot-Maschine reibungsfrei und ist deshalb reversibel, sodass ihr Arbeitszyklus sogar umgekehrt werden kann. Zeitlich rückwärts gesehen wäre sie dann wie ein Kühlschrank oder wie eine Wärmepumpe, die mithilfe der zugeführten Arbeitsmenge \( W \) den kälteren Wasserbehälter weiter abkühlt und den wärmeren Wasserbehälter weiter aufheizt. Arbeit und Wärmemengen haben dann das umgekehrte Vorzeichen, aber sämtliche Formeln von oben sind weiterhin gültig.
Aber vielleicht gibt es ja irgendeine andere Wundermaschine, die einen besseren Wirkungsgrad besitzt als unsere reversible Carnot-Maschine? Falls ja, dann könnten wir beide Maschinen zu einer neuen Maschine kombinieren, in der die Wundermaschine mit ihrer größeren Arbeits-Ausbeute eine rückwärts laufende Carnot-Maschine antreibt, wobei die Carnot-Maschine dem wärmeren Wasserbehälter genau die Wärmemenge \( Q_1 \) zurückgibt, die ihm die Wundermaschine entnimmt – der wärmere Wasserbehälter kann also sogar relativ klein sein und in die Kombi-Maschine mit eingebaut werden. Hier die Details:
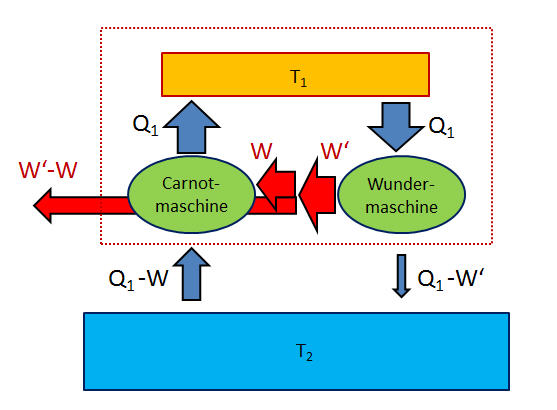
Insgesamt entnimmt unsere Wundermaschine also dem eingebauten wärmeren Wasserbehälter dieselbe Wärmemenge, die ihr unsere rückwärts laufende Carnot-Maschine wieder zuführt. Bei diesem Behälter bleibt also alles unverändert.
Dem kälteren Wasserbehälter führt die Wundermaschine die Abwärme \( Q_1 - W' \) zu, während ihm die Carnot-Maschine wieder die Wärmemenge \( Q_1 - W \) entnimmt. Es verbleibt dort also die Wärmemenge \begin{equation} (Q_1 - W') - (Q_1 - W) = - (W' - W) \end{equation} Nun soll aber die Wundermaschine mehr Arbeit \( W' \) gewinnen, als dies die normal laufende Carnot-Maschine könnte, d.h. \( W' \) ist größer als \( W \), und somit ist das Ergebnis rechts negativ. Es muss in Summe also dem kälteren Wasserbehälter eine Wärmemenge entnommen werden, nämlich genau die Wärmemenge, die als Arbeit \( W' - W \) übrig bleibt, nachdem die rückwärts laufende Carnot-Maschine ihren Teil für die Kühlarbeit abgezweigt hat. Damit hätten wir eine Kombi-Maschine konstruiert, die nichts anderes tut, als einen Wasserbehälter abzukühlen und die entnommene Wärmemenge als Arbeit verfügbar zu machen. Eine solche Maschine kann es aber nach dem zweiten Hauptsatz nicht geben, wie wir von oben wissen.
Damit ist klar: Unsere Wundermaschine mit höherem Wirkungsgrad existiert nicht, denn sonst könnten wir die verbotene Kombi-Maschine bauen. Die reversible Carnot-Maschine hat also den bestmöglichen Wirkungsgrad von allen Wärmekraftmaschinen, und jede andere Wärmekraftmaschine kann bestenfalls denselben Wirkungsgrad erreichen! Entscheiden ist dabei die Eigenschaft, dass die Carnot-Maschine reversibel ist und man sie rückwärts laufend in der Kombi-Maschine einsetzen kann.
Was geschieht nun, wenn unsere Wundermaschine, die ja maximal den Wirkungsgrad der Carnot-Maschine haben kann, ebenfalls reversibel ist? Dann können wir das ganze Argument herumdrehen und die Wundermaschine rückwärts laufen lassen, während die Carnot-Maschine vorwärts läuft. So lässt sich analog zeigen, dass die Carnot-Maschine bestenfalls denselben Wirkungsgrad hat wie die reversible Wundermaschine – insgesamt müssen beide reversible Maschinen also denselben Wirkungsgrad haben. Jede reversible Wärmekraftmaschine hat also denselben Wirkungsgrad, der zugleich der bestmögliche Wirkungsgrad aller (auch nicht-reversiblen) Wärmekraftmaschinen ist! Dabei ist es vollkommen egal, wie die Maschine gebaut ist – Hauptsache, sie arbeitet reversibel.
Ich finde es erstaunlich, wieviel Einsichten man durch solche einfachen Argumente fast ganz ohne Formeln gewinnen kann. Einzig für den konkreten Wert des Wirkungsgrades reversibler Maschinen haben wir oben die Formel \( Q_1 / T_1 = Q_2 / T_2 \) benötigt, die sich für die Carnot-Maschine aus einer konkreten Rechnung mithilfe der allgemeinen Gasgleichung ergibt (wir haben diese Standard-Rechnung nicht gezeigt). Nun haben wir aber gesehen, dass es nicht am Gas liegen kann – jede reversible Maschine hat denselben Wirkungsgrad. Es müsste also möglich sein, diese Formel auch ohne die Gasgleichung zu gewinnen – einfach durch Argumentation mit dem zweiten Hauptsatz. Das wollen wir uns im folgenden Abschnitt genauer ansehen.
Wenn wir ohne die Gasgleichung auskommen wollen, so haben zunächst wir ein Problem: Wir wissen nicht, was die Temperatur eigentlich sein soll, denn diese hatten wir oben über die mittlere kinetische Energie der Gasteilchen definiert. Alles, was wir ohne diese Definition wissen, ist, dass Wärme nach dem zweiten Hauptsatz von allein immer nur von einem wärmeren zu einem kälteren Objekt fließt. Wir brauchen also eine dazu passende Definition der Temperatur, die sich im Nachhinein idealerweise als konsistent mit der Definition über das Gas herausstellen soll. Man bezeichnet die so definierte Temperatur als absolute Temperatur oder auch als thermodynamische Temperatur.
Als erstes benötigen wir dazu einen Temperatur-Referenzpunkt \( T_s \) , wobei der Index s für standard stehen soll. Nehmen wir beispielsweise den sogenannten Tripelpunkt des Wassers – das ist diejenige eindeutige Kombination aus Druck und Temperatur, bei der eine Mischung aus Wassereis, flüssigem Wasser und Wasserdampf zugleich im thermischen Gleichgewicht existieren kann (noch früher hatte man statt dessen den Schmelzpunkt von Wasser gewählt, aber da dieser druckabhängig variiert, stellte sich der Tripelpunkt als praktikabler heraus, da hier der Druck automatisch festliegt). Nun legt man fest, dass die Temperatur des Wassers an diesem Tripelpunkt genau 273,16 Kelvin (kurz: K) betragen soll, was die Maßeinheit Kelvin festlegt. Den krummen Vorfaktor 273,16 hat man deshalb hinzugefügt, damit Temperaturdifferenzen in Kelvin später exakt mit den gewohnten Temperaturdifferenzen in Grad Celsius übereinstimmen – beide Temperaturskalen unterscheiden sich also nur durch die Wahl des Nullpunktes der Temperaturskala, während gleichsam die Gradmarken dieselben Abstände haben. Der Nullpunkt der Celsius-Skala (also Null Grad Celsius, gegeben durch den Schmelzpunkt von Wasser bei Normaldruck) liegt dann bei 273,15 K, also ganz nahe bei der Temperatur des Wasser-Tripelpunktes. Halten wir also fest: \begin{equation} T_s = 273,16 \, \mathrm{K} \end{equation} Bis ins Jahr 2019 ging man im SI-Einheitensystem übrigens genau so vor, um die Maßeinheit Kelvin festzulegen. Heute verwendet man dagegen die Boltzmannkonstante \(k\) von oben dafür, indem man ihr einen festen Wert zuweist und so die Temperatureinheit Kelvin an die Energieeinheit Joule koppelt. Genau so haben wir das oben ja über die Formel \( E_\mathrm{kin} = \frac{3}{2} k T \) für die kinetische Energie von Gasatomen auch gemacht.
Nach Festlegung der Referenz-Temperatur \( T_s \) können wir nun im Prinzip folgendes tun: Wir nehmen uns irgendeine ideale reversible Wärmekraftmaschine, beispielsweise eine Carnot-Maschine. Diese Maschine betreiben wir zwischen irgendeinem Wärmereservoir (z.B. einem Wasserbehälter), dessen Temperatur \( T \) wir definieren wollen, und einem Referenz-Wärmereservoir, das die Standardtemperatur \( T_s \) besitzt. Wir legen fest, dass die Maschine dem Referenz-Wärmereservoir eine bestimmte Wärmemenge \( Q_s \) übertragen soll (oder auch wahlweise entnimmt, denn da die Maschine reversibel ist, können wir sie nach Belieben auch rückwärts laufen lassen). Da der Wirkungsgrad nicht von der Bauweise der reversiblen Maschine abhängt, liegt dadurch auch die Wärmemenge \( Q \) eindeutig fest, die unsere Maschine dem anderen Wärmereservoir bei der Temperatur \( T \) entimmt (oder bei Rückwärtslauf an dieses Reservoir abgibt).
Nun muss bei vorgegebenen Temperaturen \( T \) und \( T_s \) die entnommene Wärmemenge \( Q \) proportional zu \( Q_s \) anwachsen, denn wir könnten beispielsweise zwei identische reversible Maschinen parallel zueinander zwischen den beiden Wasserbehältern arbeiten lassen und sie uns als eine einzige Kombi-Maschine denken, sodass sich die entnommene Wärmemenge \( Q \) und die Abwärme \( Q_s \) beide verdoppeln. Wenn \( T \) und \( T_s \) festliegen, dann hat also der Quotient \( Q/Q_s \) immer denselben Wert, egal wie groß die Wärmemenge \( Q_s \) ist, die wir an unser Referenz-Reservoir übertragen. Der Quotient \( Q/Q_s \) ist also irgendeine Funktion der Temperatur \( T \) und unserer Standard-Temperatur \( T_s \): \begin{equation} \frac{Q}{Q_s} = f(T,T_s) \end{equation} Und jetzt kommt der entscheidende Schritt: Da wir ja noch gar keine genaue Definition der Temperatur \( T \) haben, definieren wir sie nun so, dass die Funktion \( f \) möglichst einfach wird, d.h. wir definieren \( T \) durch die Beziehung \begin{equation} \frac{Q}{Q_s} = \frac{T}{T_s} \end{equation} oder anders geschrieben: \begin{equation} T = \frac{Q}{Q_s} \, T_s \end{equation} Wenn also beispielsweise die ideale Maschine an unser Standard-Reservoir die Wärmemenge \( Q_s \) gleich 1 Joule abgibt und dafür dem anderen Reservoir die doppelte Wärmemenge \( Q \) gleich 2 Joule an Wärme entnimmt (also davon 1 Joule an Arbeit abzweigt), dann hat dieses Reservoir per Definition die Temperatur von 2 mal 273,16 K gleich 546,32 K, ist also doppelt so heiß wie unser Standard-Reservoir. Wird dagegen nur \( Q \) gleich 0,5 Joule entnommen, dann liegt die Temperatur bei 136,58 Kelvin, d.h. die Maschine benötigt hier Arbeit für den Wärmetransfer ins wärmere Standard-Reservoir.
Ist das eine sinnvolle und konsistente Definition für die Temperatur? Fließt beispielsweise Wärme von alleine garantiert vom wärmeren zum kälteren Körper? Das tut sie, wie man folgendermaßen sieht:
Nach der obigen Definition ist die Temperatur eines Reservoirs größer als die Referenztemperatur, wenn die reversible Maschine eine größere Wärmemenge entnehmen muss, als sie an das kältere Referenzreservoir zurückgibt, sodass die Differenz als Arbeit zur Verfügung gestellt wird. Jede nicht-reversible Maschine hat nun einen schlechteren Wirkungsgrad als die reversible Maschine, sodass im Extremfall gar keine Arbeit übrig bleibt, sondern die komplette Wärmemenge auf das kältere Referenzreservoir übergeht – das entspricht dem reinen Wärmefluss. Will man dagegen Wärme vom kälteren in das wärmere Reservoir übertragen, so muss auch eine reversible Maschine Arbeit aufwenden, und man muss umso mehr Arbeit aufwenden, je ineffizienter die Maschine ist. Von alleine – also ohne Arbeit – fließt also gar keine Wärme von kalt nach warm.
Es gibt aber noch eine weitere Konsistenzbedingung, die man überprüfen muss, denn man kann zwei reversible Maschinen auch hintereinanderschalten, sodass sie einer dazu gleichwertigen reversiblen Maschine entsprechen. Dabei sollte die Referenz-Temperatur beliebig wählbar sein, denn wir haben ja ganz willkürlich den Tripelpunkt von Wasser als Referenz-Temperatur gewählt. Passt dann noch alles zusammen?
Machen wir es konkret, und betrachten neben unserem Standard-Wärmereservoir mit der Temperatur \( T_s \) zwei weitere Wärmereservoire 1 und 2 mit Temperaturen \( T_1 \) und \( T_2 \).
Eine reversible Maschine 1 entnimmt nun dem Reservoir 1 bei \( T_1 \) die Wärmemenge \( Q_1 \), d.h. sie gibt entsprechend der Temperaturdefinition bei \( T_s \) die Wärmemenge \( Q_s \) an das Standardreservoir ab. Genau so war ja die Temperatur \( T_1 \) definiert, wobei folgendes gelten muss: \begin{equation} \frac{Q_1}{Q_s} = \frac{T_1}{T_s} \end{equation} Eine weitere reversible Maschine 2 entnimmt nun dem Standardreservoir bei \( T_s \) genau diese Wärmemenge \( Q_s \), sodass sie entsprechend der Temperaturdefinition bei \( T_2 \) die Wärmemenge \( Q_2 \) an das Reservoir 2 abgibt (bei der Definition der Temperatur \( T_2 \) darf die reversible Maschine ja auch rückwärts laufen, da die Laufrichtung beliebig ist). Dabei gilt laut Temperaturdefinition: \begin{equation} \frac{Q_2}{Q_s} = \frac{T_2}{T_s} \end{equation} Für das Verhältnis \( Q_1 / Q_2 \) der beiden Wärmemengen gilt nach der Temperaturdefinition also \begin{equation} \frac{Q_1}{Q_2} = \frac{Q_1}{Q_s} \, \frac{Q_s}{Q_2} = \frac{T_1}{T_s} \, \frac{T_s}{T_2} = \frac{T_1}{T_2} \end{equation} Nun wirken beide Maschinen zusammen genau so wie eine einzige reversible Maschine, die bei \( T_1 \) die Wärmemenge \( Q_1 \) entnimmt und bei \( T_2 \) die Abwärme \( Q_2 \) zurückgibt. Man hätte also auch das Temperaturniveau \( T_2 \) als Referenztemperatur für die Temperaturdefinition nehmen können und hätte dann die Temperatur \( T_1 \) von Reservoir 1 über die Beziehung \begin{equation} \frac{Q_1}{Q_2} = \frac{T_1}{T_2} \end{equation} mithilfe der Kombi-Maschine definiert. Dabei wäre man auf dieselbe Temperatur \( T_1 \) für Reservoir 1 gekommen wie mit der Standard-Referenztemperatur \( T_s \) über die reversible Maschine 1 alleine.
Unsere Definition der absoluten Temperatur über reversible Wärmekraftmaschinen ist also offenbar in sich konsistent. Glücklicherweise deckt sie sich außerdem mit der Temperatur, die wir oben über die mittlere kinetische Energie der Teilchen in einem idealen Gas festgelegt hatten, denn mit der Carnot-Maschine und dem idealen Gasgesetz kamen wir ja oben auf dieselbe Beziehung zwischen Wärmemengen und Temperaturen, wie wir sie für die Definition der absoluten Temperatur verwendet haben. Es passt also alles zusammen.
Beide Temperaturdefinitionen zeigen, dass es einen absoluten Nullpunkt \( T = 0 \) für die Temperatur geben muss, bei dem die Gasteilchen keine kinetische Energie mehr besitzen bzw. bei der eine reversible Wärmekraftmaschine keine Abwärme mehr an ein entsprechend kaltes Wärmereservoir abgeben muss und die komplette aufgenommene Wärmemenge mit Wirkungsgrad \( \eta = 1 \) in Arbeit verwandeln kann. Nach dem dritten Hauptsatz der Thermodynamik (auch Nernst-Theorem genannt) kann man dem absoluten Nullpunkt zwar beliebig nahekommen, ihn aber nie ganz erreichen. Wir wollen hier nicht näher darauf eingehen.
Der Begriff der Temperatur ist damit ziemlich klar – doch was hat es mit der Entropie auf sich? Wir sind nun in der Lage, auch diesen Begriff zu definieren: Die Entropie soll mit den Wärmemengen verbunden sein, die in einer reversiblen Maschine zwischen den Wärmereservoiren und der Maschine ausgetauscht werden, wobei aber anders als bei den Wärmemengen – von denen ja Arbeit abgezweigt wird – die Entropie insgesamt erhalten bleiben soll. Damit ist klar, wie wir die Entropie definieren müssen: Wir sagen, dass in einem reversiblen Prozessschritt, in dem bei konstanter Temperatur \( T \) die Wärmemenge \( Q \) sehr langsam durch ein infinitesimales Temperaturgefälle einem Körper zufließt, zugleich die Entropie \begin{equation} \Delta S = \frac{Q}{T} \end{equation} in den Körper fließt (fließt die Wärmemenge dagegen ab, dann rechnen wir \( \Delta S \) negativ). Bei unserer reversiblen Carnot-Maschine oben fließt daher bei der isothermen Expansion in Schritt 1 die Entropie \( \Delta S_1 = Q_1/T_1 \) vom Wasserbehälter 1 in den Gaszylinder, um diesen dann bei der isothermen Kompression in Schritt 3 wieder zu verlassen, denn \begin{equation} \Delta S_1 = \frac{Q_1}{T_1} = \frac{Q_2}{T_2} = - \Delta S_2 \end{equation} wobei wir das Vorzeichen so gewählt, haben, dass Entropien positiv sind, wenn die Wärmemenge dem Gas im Zylinder zufließt. Bei der adiabatischen Expansion in Schritt 2 und der adiabatischen Kompression in Schritt 4 verändert sich die Entropie dagegen nicht, da die Schritte reversibel (also extrem langsam und reibungsfrei) erfolgen sollen und da dabei keine Wärmemengen fließen (der Gaszylinder ist also bei diesen Schritten thermisch isoliert).
Insgesamt geht beim reversiblen Carnot-Prozess also keine Entropie verloren, sondern die Entropie fließt von einem Wasserbehälter über das Gas als Zwischenstation in den anderen Wasserbehälter, wobei jeweils entsprechende Wärmemengen transportiert werden, die aber – anders als die Entropiemengen – nicht gleich sind, da ja Arbeit abgezweigt wird.
Das ist nun der Moment, in dem Carnot's ursprüngliche Idee wieder ins Spiel kommt, die wir zu Beginn des Kapitels bereits angesprochen hatten. Carnot hatte sich ja vorgestellt, dass ein unzerstörbarer Wärmestoff vom höheren zum niedrigeren Temperaturniveau gewissermaßen herunterfällt und dadurch eine Wärmekraftmaschine antreibt, so wie herabfallendes Wasser eine Wassermühle in Bewegung setzt. Wenn wir den Wärmestoff mit den Wärmemengen \( Q_1 \) und \( Q_1 \) gleichsetzen, dann funktioniert diese Idee nicht, denn die Wärmemenge bleibt ja nicht erhalten, sondern es wird Arbeit \( W \) abgezweigt: \( W = Q_1 - Q_2 \).
Wenn wir hier aber die Wärmemengen durch die Entropie ausdrücken, geschieht folgendes: \begin{align} W &= Q_1 - Q_2 = \\ & \\ &= T_1 \, \Delta S_1 + T_2 \, \Delta S_2 = \\ & \\ &= T_1 \, \Delta S_1 - T_2 \, \Delta S_1 = \\ & \\ &= (T_1 - T_2) \, \Delta S_1 \end{align} Die Arbeit einer reversiblen Wärmekraftmaschine ist also gleich dem Temperaturunterschied mal der hindurchströmenden Entropiemenge. Ganz analog ist beim Hinabstürzen von Wasser der Höhenunterschied mal dem Gewicht der herabstürzenden Wassermasse die Arbeit, die dieses Wasser dabei leisten kann. Der unzerstörbare Wärmestoff ist also nicht die Wärmemenge selber, sondern die Entropie – zumindest bei reversiblen Prozessen, bei denen diese Entropiemenge dann erhalten bleibt. Carnot lag mit seiner Idee also durchaus recht nah an der Wahrheit – ihm fehlte nur der Entropiebegriff!
Bei einer Wassermühle kann man davon sprechen, dass ein Wasserspeicher eine bestimmte Wassermenge enthält. Enthält analog ein Körper eine bestimmte Entropiemenge? Kann man von der Entropie eines Körpers sprechen, so wie man von seiner inneren Energie – nicht aber von seiner Wärmemenge – sprechen kann? Ist die Entropie so wie die Energie eine Zustandsgröße des Körpers, die nur vom makroskopischen Zustand des Körpers abhängt?
Bei einem Gas mit einer festgelegten Anzahl an Gasteilchen wäre ein solcher Zustand beispielsweise durch die Angabe von Druck \( p \) und Volumen \( V \) eindeutig festgelegt (die Temperatur ist dann über die Gasgleichung gegeben) – genau deshalb konnten wir oben die Zustandsänderungen des Gases im Gaszylinder beim Carnot-Zyklus vollständig in einem p-V-Diagramm darstellen! Wir könnten aber auch einen ganz anderen kreisförmigen Weg in dem p-V-Diagramm beschreiben, der einem anderen reversiblen Kreisprozess für das Gas entspricht – Hauptsache, wir kommen am Schluss wieder im Anfangszustand an. Diesen Weg könnten wir in viele kleine (infinitesimale) isotherme und adiabatische reversible Kompressionen und Expansionen aufteilen. Bei den adiabatischen Schritten bleibt die Entropie des Gases unverändert, während bei den isothermen Schritten, bei denen bei Temperatur \( T \) die winzige Wärmemenge \( \delta Q \) zu- oder abfließt, sich die Entropie um den winzigen Betrag \begin{equation} dS = \frac{\delta Q}{T} \end{equation} ändert. In Summe heben sich auf dem Kreisweg aber alle diese Entropieänderungen des Gases im Zylinder gegenseitig auf, so wie sie das auch beim Carnotzyklus tun. Für ein ideales Gas kann man das mithilfe der Gasgleichung explizit nachrechnen, aber man kann es auch allgemeiner zeigen – hier eine kurze Skizze des Beweises: Man pflastert dazu die umschlossene Innenfläche des Kreisweges mit winzig kleinen reversiblen Carnot-Zyklen (oder anderen kleinen reversiblen Kreiszyklen) zu. Die Entropieänderung entlang des großen Kreisweges ist nun gleich der Summe aller Entropieänderungen entlang der kleinen Carnot-Zyklen, denn da die Zyklen sich an den inneren Rändern berühren und zwei benachbarte Zyklen ihren gemeinsamen Rand entgegengesetzt durchlaufen, heben sich die Entropieänderungen der inneren Berührungskanten der Zyklen gegenseitig auf und es bleiben nur die Entropieänderungen der Ränder übrig, an denen kein anderer Mini-Zyklus anstößt – und das entspricht angenähert dem großen Kreisweg. Die Entropieänderung entlang jedes Carnot-Minizyklus ist nun Null, sodass insgesamt auch die Entropieänderung entlang des Kreisweges Null ist.
Wenn man nun zwei Punkte (Zustände) a und b auf dem Kreisweg im p-V-Diagramm (Zustandsraum) auswählt, so verbinden die beiden Teilstücke des Kreisweges diese beiden Punkte über zwei verschiedene Wege. Es ist nun egal, ob man den einen oder den anderen Weg von a nach b läuft – die Entropieänderung entlang des Weges muss dieselbe sein, denn wenn man den einen Weg von a nach b und den anderen Weg zurück von b nach a läuft, hat man ja einen Kreisweg beschritten und die beiden Entropieänderungen müssen sich gegenseitig zu Null summieren. Es ist genauso wie bei der Höhe in einem hügeligen Gelände, in der man verschiedene Wege zwischen zwei Punkten durchläuft – die Höhenänderung ist in Summe immer dieselbe, unabhängig vom Weg, sodass man jedem Punkt eine Höhe zuordnen kann. Analog kann man jedem Zustand des Gases und allgemein jedem makroskopischen Zustand eines Körpers eine Entropie zuordnen, die dieser Körper besitzt.
Für Wege im hügeligen Gelände spielen zunächst nur Höhenunterschiede eine Rolle, aber keine absoluten Höhen. Lange dachte man, das sei auch bei der Entropie so, sodass nur Entropiedifferenzen zwischen verschiedenen Zuständen relevant seien, aber keine absoluten Entropien. Erst die Quantenmechanik hat dies geändert. Hier kann man zeigen, dass die Entropie gegen Null geht, wenn die Temperatur gegen Null geht, denn dann befindet sich das gesamte System im energetischen Grundzustand (dritter Hauptsatz der Thermodynamik bzw. Nernst-Theorem) – mehr dazu weiter unten. Damit hat man einen klaren Referenzpunkt für alle Entropien, sodass man jedem Körper in einem bestimmten makroskopischen Zustand eindeutig eine Entropie zuordnen kann.
Bei all diesen Gedankengängen muss man immer aufpassen, dass man das unscheinbare Wort reversibel nicht übersieht – nur bei reversiblen Prozessen ist die Entropie erhalten! Das sind aber stark idealisierte Prozesse, bei denen es keine Reibung gibt und bei denen Wärmemengen nur durch infinitesimale Temperaturunterschiede auf Wanderung gehen. In der Realität gibt es solche Prozesse aber nicht, und die Entropie dürfte dann nicht mehr erhalten bleiben – sie taugt dann auch nicht mehr für Carnot's Vorstellung eines unzerstörbaren Wärmestoffs, der das Temperaturgefälle hinunterfällt. Was geschieht also mit der Entropie bei realen, nicht-reversiblen Prozessen?
Nehmen wir als Beispiel eine reversible Maschine und verwenden die erzeugte Arbeit \(W\), um dem kälteren Wasserbehälter vorsichtig und langsam über Reibung zusätzlich eine Wäremenge \( Q_2' = W \) und somit eine Zusatzentropie \( \Delta S_2' = Q_2'/T_2 \) zuzuführen (wie immer soll der Behälter so groß sein, dass sich seine Temperatur \( T_2 \) dabei kaum ändert). Aufgrund dieser Zusatzentropie, die durch Reibung entstanden ist, wächst die Entropie jetzt in Summe also an! Der kältere Wasserbehälter erhält mehr Entropie zugeführt, als den wärmeren Wasserbehälter verlässt. Hier lässt sich der Vorgang nicht umkehren, denn die durch Reibung aus der Arbeit \(W\) erzeugte Wärmemenge \(Q_2'\) lässt sich nicht einfach wieder komplett in Arbeit zurückverwandeln. Zusammen mit der Reibungsvorrichtung ist die Maschine jetzt irreversibel geworden!
Reibung erhöht also die Entropie, da sie Arbeit in zugeführte Wärmemengen verwandelt. Deshalb hatten wir für reversible Maschinen Reibung oben ausgeschlossen. Wie sieht es nun mit Wärmeflüssen aus, für die wir oben einen nur infinitesimalen Temperaturunterschied verlangt hatten? Was geschieht mit der Entropie, wenn eine Wärmemenge \( Q \) von einem heißeren Körper der Temperatur \( T_1 \) durch Wärmefluss (also ohne irgendwelche Maschinen) langsam, aber direkt zu einem deutlich kälteren Körper der Temperatur \( T_2 \) fließt? Die Entropie des wärmeren Körpers fällt dann um \( \Delta S_1 = - Q/T_1 \), während die Entropie des kälteren Körpers um \( \Delta S_2 = Q/T_2 \) anwächst, was in Summe die folgende Entropieänderung ergibt: \begin{align} \Delta S &= \Delta S_1 + \Delta S_2 = \\ & \\ &= - \frac{Q}{T_1} + \frac{Q}{T_2} = \\ & \\ &= Q \, \left( \frac{1}{T_2} - \frac{1}{T_1} \right) \end{align} Da \( T_1 \) größer als \( T_2 \) ist, ist \( \Delta S \) positiv, d.h. der irreversible Wärmefluss von heiß nach kalt erhöht auch hier die Entropie.
Übrigens: Ohne es zu merken, haben wir bei dieser Diskussion gerade zwei Eigenschaften für die Entropie vorausgesetzt:
Zugegeben: Beides müsste man eigentlich noch deutlich sorgfältiger begründen, aber wir wollen es hier nicht übertreiben, da viele Aspekte der Entropie sowieso sehr viel klarer werden, wenn wir erst einmal die mikroskopische Interpretation der Entropie zur Verfügung haben.
Insgesamt erhöht sich also bei irreversiblen Prozessen immer die Gesamtentropie, und nur im idealisierten Grenzfall reversibler Prozesse, bei denen die Zeitrichtung egal ist, bleibt sie konstant. Das erinnert uns an unsere Überlegungen zum Ursprung des Zeitpfeils aus dem Kapitel Was ist Zeit?: Die Richtung des Zeitpfeils wird durch das Anwachsen der Entropie definiert. Kurz: Die Zeit vergeht, wenn die Entropie ansteigt.
Wirklich verstanden haben wir den Anstieg der Entropie mit der Zeit aber bisher noch nicht, denn der Ausgangspunkt aller Überlegungen war ganz oben der zweite Hauptsatz gewesen, nach dem eine Wärmemenge von alleine mit zunehmender Zeit immer von warm nach kalt fließt – da war im Grunde alles schon eingebaut, und wir haben den Wärmefluss nur kunstvoll in eine anwachsende Entropie übersetzt. Der Entropiebegriff erscheint dabei wie eine abstrakte Rechengröße, die zwar nützlich, aber zugleich auch irgendwie unanschaulich ist. Was genau soll Entropie eigentlich sein?
Als Begründung für den zweiten Hauptsatz hatten wir ganz oben ein mikroskopisches Bild angeführt: Der Wärmefluss sorgt dafür, dass sich die Energie im Mittel gleichmäßig und damit maximal zufällig auf die einzelnen Teilchen verteilt. Der Zustand mit ausgeglichener Temperatur scheint irgendwie wahrscheinlicher zu sein als der Anfangszustand mit unterschiedlicher Temperatur, und es ist sehr unwahrscheinlich, dass sich die Teilchenenergien von alleine wieder so unterschiedlich verteilen wie zuvor. Der Wärmefluss verwandelt also einen unwahrscheinlichen Zustand in einen sehr viel wahrscheinlicheren Zustand, wobei zugleich die Entropie des Zustands ansteigt. Ob die Entropie womöglich ein Maß für die Wahrscheinlichkeit des Zustands ist? Das ist genau die richtige Idee, die uns zu einer mikroskopischen Interpretation der Entropie führen wird.
Bisher war ein Zustand immer ein makroskopischer Zustand (kurz Makrozustand), der sich durch wenige makroskopische Parameter vollständig beschreiben lässt. Bei einem idealen Gas war das beispielsweise seine innere Energie, sein Volumen und die darin enthaltene Gasmenge bzw. Teilchenzahl. Bei fester Gasmenge kann man alternativ auch beispielsweise Druck und Volumen verwenden, so wie wir das oben im p-V-Diagramm getan haben. Die Entropie ist dann durch diesen Makrozustand vollständig festgelegt – eben eine Zustandsgröße.
Um die Wahrscheinlichkeit ins Spiel zu bringen, müssen wir die mikroskopische Struktur des Körpers bzw. Gases betrachten, also die genauen Details, wo sich die vielen Gasteilchen befinden und wie sie sich bewegen, also wie sich die Energie auf die Teilchen verteilt. Wir müssen also die Mikrozustände betrachten, die all diese Informationen beinhalten.
Nun benötigt man für einen Mikrozustand sehr viel mehr Informationen als für einen Makrozustand, der sich bei einem Gas mit fester Teilchenzahl mit nur zwei Zahlen (Energie und Volumen oder alternativ beispielsweise Druck und Volumen) vollständig beschreiben lässt. Daher lässt sich der Makrozustand relativ leicht bestimmen, während es vollkommen aussichtslos ist, den genauen Mikrozustand eines makroskopischen Körpers mit beipielsweise 1020 Teilchen aufzudecken. Außerdem verändert sich der Mikrozustand ständig, da sich kein makroskopischer Körper vollkommen von seiner Umgebung isolieren lässt – selbst im luftleeren Weltraum würde er Photonen abstrahlen oder aufnehmen. Man kann sich daher vorstellen, dass sich der Mikrozustand ständig ändert, wobei zufällig alle möglichen erreichbaren Mikrozustände vorkommen, die mit den gegebenen Randbedingungen verträglich sind. Dabei kann sich auch der Makrozustand verändern, der über gewisse statistische Mittelwerte (beispielsweise die mittlere Energieverteilung) der gerade auftretenden Mikrozustände gegeben ist. Irgendwann ändert sich der Makrozustand dann nicht mehr – das thermische Gleichgewicht ist nun erreicht und die Energie ist beispielsweise maximal zufällig auf die Teilchen verteilt. Dabei wird im thermischen Gleichgewicht derjenige Makrozustand auftreten, der die meisten Mikrozustände umfasst. Die Entropie wird also mit der Zahl der Mikrozustände – nennen wir sie \( \Omega \) – zusammenhängen, die ein Makrozustand umfasst, d.h. die zu dessen makroskopischen Parametern passen.
Wie zählt man diese Mikrozustände? Das ist tatsächlich ein Problem, das erst durch die Quantenmechanik wirklich zufriedenstellend gelöst werden konnte. In der Quantenmechanik besitzt nämlich jeder makroskopische Körper eine große Anzahl klar definierter Quantenzustände, die beispielsweise jeweils eine eindeutig definierte Energie \( E_n \) aufweisen, wobei der Index \( n \) die Nummer des Quantenzustands kennzeichnet. Nun besitzt auch ein Makrozustand eine bestimmte makroskopische Energie \( E \), die wir oben auch als innere Energie \( U \) bezeichnet hatten. Diese Energie ist dabei aber nur makroskopisch festgelegt, d.h. die winzigen Energiefluktuationen, die aufgrund der unvermeidlichen mikroskopischen Wechselwirkungen mit der Umgebung ständig auftreten, spielen makroskopisch keine Rolle. Die makroskopische Energie \( E \) ist also nur bis auf eine gewisse Fluktuationsunschärfe \( \delta E \) festgelegt, die so klein sein muss, dass man sie makroskopisch nicht bemerkt. Ein typischer Wert für \( \delta E \) wären beispielsweise 10− 12 eV (siehe Die Symmetrie der Naturgesetze, Kapitel 7.1 Was ist Entropie?), was deutlich kleiner ist als die mittlere Energie, die ein einzelnes Teilchen im Körper typischerweise besitzt.
Nun liegt der Energieabstand zwischen den einzelnen Mikrozuständen eines makroskopischen Körpers normalerweise weit unterhalb dieser Fluktuations-Unschärfe \( \delta E \), denn die Energien \( E_n \) der unzähligen Mikrozustände liegen extrem dicht zusammen und bilden fast ein Energie-Kontinuum. Daher liegen selbst in einem makroskopisch kleinen Energieintervall \( \delta E \) um die innere Energie \( E \) herum noch sehr viele Mikrozustände, sodass die Zahl \( \Omega \) dieser Mikrozustände sehr groß ist – ein typischer Wert wäre ganz grob \(10^N \), wobei \( N \) die Teilchenzahl des Körpers ist, die selbst schon bei sehr großen Werten wie beispielsweise \( N = 10^{20} \) liegt.
Nun ist die Zahl \( \Omega \) der Mikrozustände ungefähr proportional
zum Unschärfe-Intervall \( \delta E \), das wir nur grob beschrieben haben als
makroskopisch klein, aber mikroskopisch groß.
Entsprechend ungenau ist auch die Zahl \( \Omega \) selbst definiert.
Doch wir werden gleich sehen, dass dies vollkommen ausreicht, denn es wird
nicht auf die Zahl \( \Omega \) selbst ankommen, sondern nur auf ihre ungefähre
Größenordnung, also auf die Anzahl ihrer Dezimalstellen, die grob etwa
gleich der Teilchenzahl \( N \) ist. Bei \( N = 10^{20} \) hätten wir es also bei \( \Omega \)
mit rund 1 00 000 000 000 000 000 000 (hundert-Milliarden-Milliarden) Dezimalstellen zu tun.
Würde man ein solches \( \Omega \) als Buchserie drucken wollen, so käme man bei rund 2000 Zeichen pro
Buchseite und 500 Seiten pro Buch auf 1014 Bücher.
Bei 500 Gramm pro Buch würden diese Bücher insgesamt 50 Milliarden Tonnen wiegen.
Damit ist klar: Man wird eine solche Zahl niemals ausdrucken können.
\( \Omega \) kann auch locker um einen Faktor von beispielsweise einer Milliarde variieren,
ohne dass sich die Zahl der Dezimalstellen dadurch nennenswert ändert – es wären
nur 9 Dezimalstellen mehr oder weniger, was kaum zu bemerken wäre.

Wie hängt die Entropie eines Makrozustandes nun konkret mit der Anzahl \( \Omega \) der damit verträglichen Mikrozustände zusammen? Dazu betrachten wir zwei Körper mit Temperaturen \( T_1 \) und \( T_2 \), wobei der Makrozustand des ersten Körpers \( \Omega_1 \) Mikrozustände umfasst, während es bei dem zweiten Körper \( \Omega_2 \) Mikrozustände sind.
Beide Körper zusammen bilden nun ebenfalls ein (zusammengesetztes) makroskopisches System,
dessen Makrozustand allerdings durch zwei Temperaturen \( T_1 \) und \( T_2 \)
beschrieben werden muss – ein Zeichen dafür, dass es sich noch nicht im thermischen
Gleichgewicht befindet. Jeder Mikrozustand dieses Systems besteht nun
aus je einem Mikrozustand für den ersten und den zweiten Teilkörper, sodass
wir insgesamt
\begin{equation}
\Omega = \Omega_1 \, \Omega_2
\end{equation}
Mikrozustände im zusammengesetzten System vorliegen haben.
Die Entropie dieses Systems muss jedoch die Summe der beiden Entropien
der Teilsysteme sein, denn die Entropie ist eine additive (extensive) Größe – siehe oben.
Es muss also
\begin{equation}
S = S_1 + S_2
\end{equation}
gelten. Außerdem soll die Entropie mit wachsender Zustandszahl ebenfalls anwachsen.
Daraus ergibt sich, dass die Entropie proportional zum
Logarithmus der Zustandszahl sein muss, also proportional zur
Anzahl an Dezimalstellen in der Zustandszahl – genau wie oben bereits angesprochen.
Es hat sich als günstig erwiesen, nicht den dekadischen, sondern den natürlichen
Logarithmus \( \ln \) zu verwenden. Den Proportionalitätsfaktor bestimmt man so, dass
alle obigen Eigenschaften von Entropie und Temperatur
wieder zutreffen – insbesondere auch der
Zusammenhang zwischen mittlerer Teilchenenergie und Temperatur im idealen Gas,
bei dem die Boltzmannkonstante \( k \) auftritt.
Dabei stellt sich heraus, dass der richtige Proportionalitätsfaktor eben diese
Boltzmannkonstante \( k \) ist:
\begin{equation}
S = k \, \ln \Omega
\end{equation}
Wie der Name des Proportionalitätsfaktors vermuten lässt, stammt diese
bahnbrechende Erkenntnis vom
österreichischen Physiker Ludwig Boltzmann, der sie
um das Jahr 1880 (allerdings noch ohne Bezug zur Quantenmechanik)
aufstellte und der damit erstmals eine Verbindung zwischen
der mikroskopischen Materiestruktur und ihren makroskopischen thermodynamischen
Eigenschaften schuf.
Max Planck ließ diese berühmte Formel
auf dem Grabstein Boltzmanns auf dem Wiener Zentralfriedhof
eingravieren:


Rechts: Boltzmanns Grabstein mit seiner berühmten Entropieformel (dort als \( S = k \log W \) geschrieben).
Quellen:
Wikimedia Commons File:Boltzmann Ludwig Dibner coll SIL14-B5-06a.jpg, dort public domain,
Wikimedia Commons File:Zentralfriedhof Vienna - Boltzmann.JPG,
Foto von User:Daderot,
Creative Commons Attribution-Share Alike 3.0 Unported license
Thermodynamische Begriffe wie Entropie oder Temperatur haben demnach einen grundlegend statistischen Charakter. So ist der zweite Hauptsatz der Thermodynamik eine reine Wahrscheinlichkeitsaussage. Nichts verbietet es, dass die Entropie eines Körpers von alleine signifikant absinkt, aber wir werden es praktisch nie beobachten. Wenn man ein Glas Wasser in den Ozean schüttet und später wieder ein Glas Wasser aus dem Ozean schöpft, dann wird ja analog auch kein Mensch erwarten, dass man darin genau dieselben Moleküle wiederfindet, die man zuvor hineingeschüttet hat. So etwas wird nach menschlichem Ermessen nie geschehen, aber streng verboten ist es nicht. Insofern sind die statistischen Aussagen der Thermodynamik zwar nicht absolut sicher, aber in jedem praktischen Sinn sind sie dennoch genauso sicher wie alle andere Naturgesetze und wir können uns voll und ganz auf sie verlassen.
Man kann Boltzmanns Entropieformel auch als neue und grundlegendere Definition der Entropie auffassen. Anders als die oben über reversible Prozesse definierte Entropie besitzt Boltzmanns Entropie einen klaren Referenzpunkt, nämlich den energetischen Grundzustand: Wenn die Energie des Systems sich auf seinem Minimalwert befindet, dann gibt es nur noch einen einzigen Mikrozustand – den quantenmechanischen Grundzustand – und die Entropieformel ergibt den Wert Null für die Entropie (dritter Hauptsatz der Thermodynamik).
Wenn man Boltzmanns Entropieformel als Basis verwendet, so kann man aus ihr alle anderen thermodynamischen Größen ableiten. Die Temperatur \( T \) definiert man entsprechend als die (partielle) Ableitung der Entropie nach der (inneren) Energie \( E \) (oben auch \( U \) genannt) bei ansonsten konstanten äußeren Parametern wie Volumen oder Teilchenzahl: \begin{equation} \frac{1}{T} = \frac{dS}{dE} \end{equation} oder umgestellt \( dS = dE / T \). Da bei konstanten äußeren Parametern eine Energieänderung \(dE\) (oder \(dU\) ) nur durch einen Wärmefluss \( \delta Q \) erfolgen kann (also \( dE = \delta Q \) ), entspricht diese Temperaturdefinition unserer obigen Formel \( dS = \delta Q / T \).
Der Kehrwert \( 1/T \) der Temperatur \( T \) sagt uns also, wie schnell die
Entropie mit zugeführter Wärmemenge
ansteigt. Ein Wärmefluss wird also immer von einem Körper mit
kleinerem \( 1/T \)-Wert zu dem mit größerem \( 1/T \)-Wert erfolgen, da dadurch die Entropie
insgesamt anwächst. Der Körper mit kleinerem \( 1/T \)
ist in diesem Sinn also der heißere Körper,
was normalerweise einem größeren \(T\)-Wert entspricht –
die Temperatur und damit \( dS/dE \) ist nämlich
normalerweise positiv, da die Dichte der Mikrozustände mit steigender Energie stark anwächst,
denn eine wachsende Gesamtenergie \( E \) hat zunehmend mehr Möglichkeiten, sich auf die einzelnen
Freiheitsgrade (Teilchen) zu verteilen.
Die Entropie wächst also normalerweise bei zugeführter Wärmemenge, so wie wir dies
oben auch immer vorausgesetzt hatten. Allerdings wird dieses Entropiewachsum mit zunehmendem
Wert der bereits vorhandenen inneren Energie \( E \) normalerweise immer kleiner:
Bei idealen Gasen ist beispielsweise \( 1/T \) proportional zu \( 1/E \), also \( T \) proportional zu \( E \),
sodass die Temperatur proportional zur mittleren Teilchenenergie anwächst (siehe
unsere erste Temperaturdefinition über das ideale Gas ganz oben).
Hier macht sich bemerkbar, dass die Entropie wegen des Logartihmus nur die Stellenanzahl
der Zustandszahl \( \Omega \) reflektiert – \( \Omega \) selbst wächst zwar normalerweise bei wachsender
Energie \( E \) eines Körpers rasant an, aber die Stellenanzahl von \( \Omega \) nimmt doch
immer weniger schnell zu.
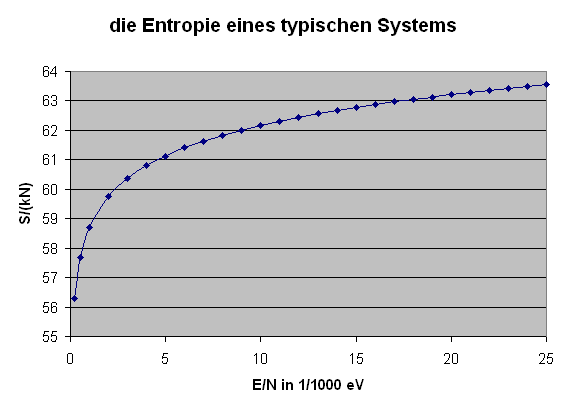
In ganz besonderen Fällen kann die Entropie bei Wärmezufuhr auch sinken,
was einer negativen Temperatur entspricht. Dieser Sonderfall tritt dann auf, wenn die einzelnen
Freiheitsgrade des Systems nur eine begrenzte Energiemenge aufnehmen können.
Es gibt daher irgendwann immer weniger Möglichkeiten, wie die weiter zugeführte Energie noch
im System untergebracht und auf die Freiheitsgrade verteilt werden kann, denn viele Freiheitsgrade
haben dann bereits ihre Energiegrenze erreicht.
Schließlich ist dann eine Maximalenergie erreicht,
bei der alle Freiheitsgrade mit Energie komplett gefüllt sind – das System befindet sich
dann eindeutig im Mikrozustand maximaler Energie und die Entropie ist wieder Null,
so wie sie das auch im Grundzustand minimaler Energie ist.
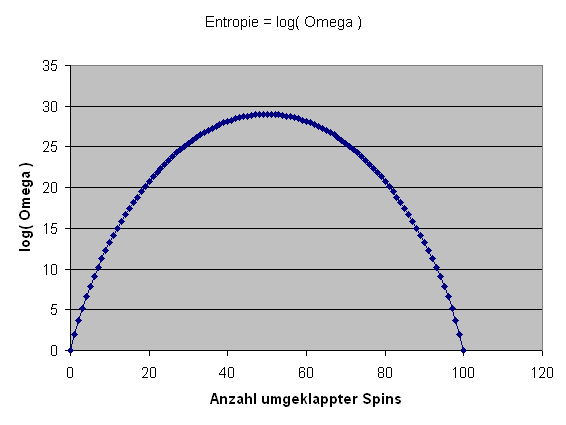
Es gäbe noch sehr viel mehr über die Entropie zu erzählen, aber wir wollen hier nicht allzu weit in die Details vorstoßen, sondern nur noch einige Kernpunkte berühren: So spiegelt Boltzmann's Entropieformel \( S = k \, \ln \Omega \) letztlich nur einen – wenn auch zentralen – Spezialfall wieder, bei dem die äußeren extensiven Parameter (Energie, Volumen, Teilchenzahl) bis auf das winzige Interval \( \delta E \) für die unvermeidlichen Energiefluktuationen fest vorgegeben sind. In diesem Fall können wir davon ausgehen, dass alle Mikrozustände im thermischen Gleichgewicht gleich häufig auftreten, denn es gibt keinen Grund, warum ein Mikrozustand gegenüber einem anderen Mikrozustand bevorzugt sein sollte. Mit anderen Worten: Wir besitzen in diesem Makrozustand im thermischen Gleichgewicht nur minimale Informationen über die Mikrozustände – alle sind gleich wahrscheinlich.
Man kann jedoch den Makrozustand auch etwas anders definieren und beispielsweise nicht die Energie vorgeben, sondern durch Kontakt mit einem äußeren großen Wärmebad die Temperatur festlegen. Dadurch legt man letztlich die mittlere Energie fest, wobei Energiefluktuationen erlaubt sind; diese sind dabei umso kleiner, je größer das betrachtete System ist. In diesem System ist nun nicht mehr jeder Mikrozustand gleich wahrscheinlich, und die Entropie muss etwas allgemeiner definiert werden als \begin{equation} S = - k \, \sum_n P_n \, \ln P_n \end{equation} (auch von-Neumann Entropie genannt) wobei die Summe über alle erreichbaren Mikrozustände geht und \( P_n \) die Wahrscheinlichkeit angibt, mit der der Mikrozustand Nummer \( n \) in dem gegebenen Makrozustand auftritt. Die Entropie ist also im Wesentlichen der negative Mittelwert der logarithmierten Wahrscheinlichkeit für die Mikrozustände, oder anders ausgedrückt: Die Entropie ist proportional zur mittleren Stellenzahl hinter dem Komma für die Mikrozustands-Wahrscheinlichkeiten. Je seltener die verschiedenen Mikrozustände im Mittel also auftreten, umso größer ist die Entropie.
Mit dieser erweiterten Entropiedefinition stellt man sicher, dass die Entropie wieder eine additive Größe ist. Bei gleicher Wahrscheinlichkeit \( P_n = 1/\Omega \) für alle Mikrozustände ergibt sich außerdem wieder Boltzmann's Formel \( S = k \, \ln \Omega \) von oben. Mehr dazu siehe Die Symmetrie der Naturgesetze, Kapitel 7.1 Was ist Entropie?.
Diese erweiterte Entropiedefinition kann man mit dem Informationsbegriff in Beziehung setzen (siehe Die Symmetrie der Naturgesetze, Kapitel 7.2 Entropie und Information sowie Shannon'sche Informationsentropie), sodass man in gewissem Sinn sagen kann:
Die Entropie misst also unser Informationsdefizit über die mikroskopische Beschaffenheit eines Systems, von dem wir nur wenige makroskopische Parameter kennen. Diese Information ist durch den unvermeidbaren Kontakt mit der Umgebung gleichsam verloren gegangen; sie ist delokalisiert worden und in die Umgebung abgewandert, aus der sie sich nicht mehr zurückgewinnen lässt – genau darin liegt die Irreversibilität dieses Vorgangs. Der zweite Hauptsatz besagt in diesem Sinne, dass bei einem makroskopischen System solange Information in die Umgebung abwandert, bis wir nur noch das Wissen über seinen Makrozustand besitzen. Genau diese unvermeidbare Delokalisierung von Information ist der Mechanismus, der Vergangenheit und Zukunft unterscheidet und der die Zeit zum fließen bringt.
Zum Schluss dieses Kapitels wollen wir noch einen kurzen Blick auf eine ganz besondere Frage werfen: Wieviel Entropie passt eigentlich in ein kugelförmiges Raumvolumen hinein? Da Entropie eine extensive (also additive) Größe ist, sollte sie anwachsen, wenn wir immer mehr Materie in das Raumvolumen hineinpressen. Irgendwann wird die Materiedichte dabei so groß, dass ein Schwarzes Loch entsteht. Wenn bei weiterer Materiezufuhr das Schwarze Loch mit seinem Ereignishorizont schließlich das Volumen komplett ausfüllt, dann ist das Maximum erreicht: Mehr Materie passt nicht in das Raumvolumen hinein, denn bei weiterer Materiezufuhr benötigt das Schwarze Loch auch mehr Raum, da sein Ereignishorizont anwächst. Zugleich ist auch das Maximum für die Entropie erreicht: Mehr Entropie kann kann man in dem Raumvolumen nicht unterbringen. Bei hinreichend kleinem Volumen ist ein Schwarzes Loch die Materieform mit der weitaus größten Entropie (siehe Die Symmetrie der Naturgesetze, Kapitel 7.3 Die Entropie schwarzer Löcher). Das liegt auch daran, dass sich der Makrozustand eines Schwarzen Lochs mit nur drei Zahlen vollständig beschreiben lässt: Masse, Ladung und Drehimpuls, wobei die Ladung normalerweise Null ist. Alle anderen Informationen über die verschluckte Materie sind verschwunden – kein Wunder also, dass hier das Informationsdefizit und damit die Entropie maximal sind.
Da nun die Entropie im Universum normalerweise immer weiter anwächst, wird sich bei nicht allzu kleiner Materiedichte schließlich alle Materie in Schwarzen Löchern vereinen. Erst wenn bei fortschreitender Expansion des Universums die mittlere Materiedichte immer weiter absinkt, werden die Schwarzen Löcher nach Ewigkeiten zerstrahlen, denn in einem sehr großen Raum stellen selbst Schwarze Löcher nicht mehr das Maximum der Entropie dar. Ein kaum messbarer Hauch aus Teilchen wird den Raum dann noch durchdringen und den Materiezustand mit der größten Entropie darstellen. Wie in Michael Endes Unendlicher Geschichte wird sich unsere Welt gleichsam im Nichts verlieren – ein nicht sehr tröstlicher Ausblick, der aber erst nach sehr sehr langer Zeit erreicht sein wird; wir sollten also nicht allzu beunruhigt sein.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 17 February 2023