Kapitel 5
Ungelöste Rätsel

6    Mathematische Unendlichkeiten

• Kurze Wiederholung zum Einstieg
• Kardinalzahlen
• Unendliche Kardinalzahlen
• Unerreichbare Kardinalzahlen
• Das Mengenuniversum V
• Erweiterungen der ZFC-Mengenlehre

Kurze Wiederholung zum Einstieg

Es gibt heute ein allgemein akzeptiertes axiomatisches Fundament der Mathematik: die Mengenlehre, so wie sie in den Zermelo-Fränkel-Axiomen festgelegt ist (oft abgekürzt als ZF ). Meist nimmt man noch das Auswahlaxiom hinzu und kürzt dieses Axiomensystem mit ZFC ab, wobei das C für choice steht. Die Details dazu hatten wir in den Kapiteln 4.1 bis 4.4 kennengelernt (speziell in Kapitel 4.2 Die Axiome der Mengenlehre ).

Die Mengenlehre ist extra dazu gebaut, um mit Unendlichkeiten umzugehen. Besonders gut schafft sie das bei der Unendlichkeit der natürlichen Zahlen. Sie kann die Gesamtheit der natürlichen Zahlen viel besser erfassen als die Peano-Arithmetik, die sich nur zählend von Zahl zu Zahl vorwärtshangeln kann. Das liegt daran, dass man in der Mengenlehre über die Menge der natürlichen Zahlen insgesamt sprechen kann, und darüber hinaus sogar über alle Teilmengen der natürlichen Zahlen, also über alle ihre Eigenschaften. Das ist speziell bei der Induktion wichtig und führt dazu, dass alle Modelle der natürlichen Zahlen in der Mengenlehre gleichwertig zueinander sind (siehe Kapitel 4.4 ). So wundert es nicht, dass man im Rahmen der Mengenlehre Dinge über die natürlichen Zahlen beweisen kann, die für die Peano-Arithmetik unentscheidbar sind. Als Beispiel dafür haben wir die Goodsteinfolgen in Kapitel 4.6 kennengelernt.

So wie die Peano-Arithmetik Schwierigkeiten mit der Unendlichkeit der natürlichen Zahlen hat, so hat die Mengenlehre Schwierigkeiten mit der Unendlichkeit von komplizierteren Mengen. Mit der Unendlichkeit der natürlichen Zahlen kommt sie dagegen gut zurecht – es müssen schon gravierendere Unendlichkeiten sein, die Probleme machen. Die überabzählbare Unendlichkeit des Kontinuums (die reellen Zahlen) ist gravierend genug. So wissen wir aus Kapitel 4.4, dass es abzählbare Modelle für die ZFC-Axiome der Mengenlehre gibt. In diesem Modell wären die reellen Zahlen abzählbar, wobei dies aber innerhalb des Modells nicht erkennbar ist, sondern nur gleichsam von außen. Ein anderes Problem, das mit reellen Zahlen zusammenhängt, ist die Kontinuumshypothese (siehe Kapitel 4.3 ). Nach dieser Hypothese gibt es keine unendliche Menge, die sich nicht komplett durchnummerieren lässt, die sich aber auch nicht eins-zu-eins den reellen Zahlen zuordnen lässt, ohne dass reelle Zahlen übrig bleiben. Es gibt also keine Menge mit einer Mächtigkeit zwischen den natürlichen und den reellen Zahlen. Insbesondere gibt es nach der Hypothese auch keine entsprechende Teilmenge der reellen Zahlen. Kann man das beweisen? Die ZFC-Axiome können dies jedenfalls nicht, denn die Kontinuumshypothese ist dort unentscheidbar! Die Mächtigkeit einer Menge kann man auch als Grad ihrer Unendlichkeit betrachten. Die Mengenlehre ZFC weiß nicht genug über Mengen, um solche Fragen beantworten zu können. Speziell weiß sie auch nicht genug über die Teilmengen der reellen Zahlen, also über die Eigenschaften der reellen Zahlen. ZFC weiß nicht, ob man reelle Zahlen so heraussuchen kann, dass es überabzählbar viele sind, aber nicht genug, um eine Eins-zu-Eins-Zuordnung zu allen reellen Zahlen aufstellen zu können. Nimmt man beispielsweise das überabzählbare Intervall der reellen Zahlen zwischen $-\pi /2$ und $\pi /2$ heraus, so kann man das problemlos Eins-zu-Eins den reellen Zahlen zuordnen, beispielsweise mit der Tangens-Abbildung $\tan x$. Ein Intervall enthält also schon zu viele reelle Zahlen, um ein Gegenbeispiel zur Kontinuumshypothese zu sein.

In Kapitel 4.3 haben wir einige Möglichkeiten kennengelernt, dieses fehlende Wissen in ZFC durch neue Axiome zu ergänzen. So kann man das Konstruierbarkeitsaxiom hinzufügen, das nur Mengen zulässt, die in einem bestimmten Sinn aus einfacheren Mengen konstruierbar sind (siehe Wikipedia: Constructible universe ). Für solche Mengen ist die Kontinuumshypothese beweisbar, d.h. es gibt keine konstruierbare Menge mit einer Mächtigkeit zwischen den natürlichen und den reellen Zahlen. Außerdem ist das Auswahlaxiom für konstruierbare Mengen automatisch richtig, braucht also nicht gefordert zu werden.

Eine andere Möglichkeit aus Kapitel 4.3 war das Axiom der Determiniertheit, welches das Auswahlaxiom ersetzt (es verträgt sich nämlich nicht mit diesem). Das Axiom hat etwas mit einem unendlichen Spiel zweier Spieler zu tun, die abwechselnd die einzelnen Dezimalstellen (oder Binärstellen) einer Zahl wählen dürfen. Der erste Spieler versucht dabei, zu erreichen, dass die entstehende Zahl zu einer vorgegebenen Menge gehört, während der zweite Spieler das verhindern möchte. Kann der erste Spieler es immer erreichen, dass die entstehende Zahl zur Menge gehört, oder kann der zweite Spieler dies immer verhindern, so spricht man von einer determinierten Menge. So ist jede abzählbare Menge determiniert, denn der zweite Spieler kann mit dem Cantorschen Diagonalverfahren immer verhindern, dass die im Spiel entstehende Zahl zur Menge gehört. Das Axiom der Determiniertheit fordert nun, dass nur determinierte Mengen erlaubt sind. Und wieder kann man in diesen Mengen die Kontinuumshypothese beweisen, d.h. eine fragliche Menge zwischen den natürlichen und den reellen Zahlen kann auch nicht determiniert sein.

Sowohl das Konstruierbarkeitsaxiom als auch das Axiom der Determiniertheit beschränken die mögliche Komplexität von Mengen, also in gewissem Sinn die möglichen Unendlichkeiten. Man kann aber auch versuchen, diese Unendlichkeiten zuzulassen und eine Art Überblick über sie zu gewinnen (Stichwort deskriptive Mengenlehre, siehe Kapitel 4.3 ). Das kann man beispielsweise mit Hilfe der sogenannten Kardinalzahlen tun. Schauen wir uns das in diesem Kapitel etwas näher an!

Kardinalzahlen

Kardinalzahlen sind ein Maß für die Mächtigkeit von Mengen. Sie beantworten die Frage, welche von zwei Mengen in einem bestimmten Sinn die größere ist. Das tun sie auch bei unendlichen Mengen, was beispielsweise für die Kontinuumshypothese nützlich ist.

Zum Vergleich: Ordinalzahlen, wie wir sie in Kapitel 4.6 bei den Goodsteinfolgen kennengelernt haben, dienen zur Positionsbestimmung in einer geordneten Menge, die auch größer als die natürlichen Zahlen sein kann. Wichtig ist hier immer die Frage: Welches Element steht weiter rechts, hat also die größere Ordinalzahl? Bei endlichen Mengen gibt es keinen wesentlichen Unterschied zwischen Kardinalzahl und Ordinalzahl, denn die Ordinalzahl (Nummer) des letzten Elementes ist gleich der Gesamtanzahl der Elemente der Menge, also gleich der Kardinalzahl. Bei unendlichen Mengen dagegen entsprechen Kardinalzahlen und Ordinalzahlen zwei unterschiedlichen Konzepten, mit der Unendlichkeit umzugehen. Details siehe weiter unten.

Die Idee, die Mächtigkeit unendlicher Mengen zu messen, kennen wir vom Begriff der Abzählbarkeit her (siehe Kapitel 4.1 ). Wir wollen die Mächtigkeit von unendlichen Mengen so definieren, dass überabzählbar unendliche Mengen wie die reellen Zahlen mächtiger als abzählbar unendliche Mengen sind. Die reellen Zahlen sind also mächtiger als die natürlichen oder die rationalen Zahlen. Das leuchtet ein! Dagegen sollen alle abzählbar unendlichen Mengen gleich mächtig sein. Die natürlichen und die rationalen Zahlen wären demnach gleich mächtig, da man letztere abzählen kann:

Das ist gewöhnungsbedürftig, da die natürlichen Zahlen eine Teilmenge der rationalen Zahlen sind. Man kann zu den rationalen Zahlen sogar noch abzählbar viele reelle Zahlen hinzunehmen, beispielsweise die algebraischen Zahlen, die Nullstellen von abzählbar vielen Polynomen sind. Die Mächtigkeit der Menge bleibt dieselbe. Bei unendlichen Mengen kann es also passieren, dass eine unendliche Teilmenge gleich mächtig zur Gesamtmenge ist.

Halten wir diese Idee fest:

Mächtigkeit von Mengen: Zwei Mengen $A$ und $B$ sind gleich mächtig, wenn es eine Eins-zu Eins-Zuordnung (Bijektion) zwischen den Elementen der beiden Mengen gibt. Eine Menge $A$ ist weniger mächtig als eine Menge $B$, wenn es nur eine Eins-zu Eins-Zuordnung (Bijektion) von $A$ zu einer echten Teilmenge von $B$ gibt, nicht aber zur gesamten Menge $B$. Es bleiben also zwangsläufig Elemente von $B$ übrig. Man schreibt auch $A<B$.

Im Grunde kennen wir das schon von der Kontinuumshypothese aus Kapitel 4.1 her. Wir haben es hier nur noch einmal explizit aufgeschrieben.

Nun zu den Kardinalzahlen: Sie sind keine Zahlen im engeren Sinn, sondern sie sind Äquivalenzklassen von gleich mächtigen Mengen. Man fasst also alle gleich mächtigen Mengen zusammen und kann sich dann eine davon als typischen Repräsentanten für die Kardinalzahl aussuchen. Nennen wir diesen Repräsentanten $A$. Dann schreiben wir für die Kardinalzahl aller zu $A$ gleich mächtigen Mengen einfach $|A|$ , d.h. $|A|$ ist die Äquivalenzklasse aller Mengen, die die gleiche Mächtigkeit wie $A$ aufweisen. Oft werden wir auch einfach die Menge $A$ selbst als Kardinalzahl verwenden, wenn sie ein typischer Vertreter der Äquivalenzklasse ist. Meist verwendet man als typischen Vertreter der Äquivalenzklasse die kleinste Ordinalzahl mit der geforderten Mächtigkeit. Für die abzählbaren unendlichen Mengen wählt man beispielsweise die Menge der natürlichen Zahlen $\mathbb{N}$ als Repräsentanten. Die Kardinalzahl (Äquivalenzklasse) der abzählbaren unendlichen Mengen wäre dann $|\mathbb{N}|$, aber oft schreiben wir auch einfach $\mathbb{N}$. Halten wir fest:

Kardinalzahlen: Die Kardinalzahl $|A|$ einer Menge $A$ ist die Äquivalenzklasse aller Mengen, die die gleiche Mächtigkeit wie $A$ besitzen. $A$ kann man dann als Repräsentant dieser Äquivalenzklasse ansehen.

Dabei haben wir eine Feinheit außer Acht gelassen: Streng genommen gibt es die Menge aller Mengen mit gleicher Mächtigkeit wie $A$ formal in der ZFC-Mengenlehre nicht. Daher ist diese Äquivalenzklasse entweder keine Menge (sondern eine Klasse), oder aber man muss gewisse Einschränkungen machen. Das kennen wir bereits von den Ordinalzahlen aus Kapitel 4.6: Auch die Menge aller Ordinalzahlen gibt es nicht.

Warum spricht man bei Kardinalzahlen gerne von verallgemeinerten Zahlen? Bei endlichen Mengen mit $n$ Elementen ist der Fall klar: Man nimmt als Repräsentanten der Äquivalenzklasse die Menge $\{0,1,...,n-1\}$ , und diese Menge ist zugleich die Mengendarstellung der Zahl $n$ selbst (siehe Kapitel 4.4 ). Die Kardinalzahl einer endlichen Mengen kann man also durch die Zahl ihrer Elemente repräsentieren. Bei unendlichen Mengen geht das natürlich nicht mehr, aber man kann immerhin analog zu den natürlichen Zahlen formale Rechenoperationen auf den zugehörigen Kardinalzahlen definieren:

Formales Rechnen mit Kardinalzahlen: Wir starten mit zwei disjunkten Mengen $A$ und $B$, d.h. $A$ und $B$ sollen keine gemeinsamen Elemente haben. Dann definieren wir: $$\begin{array}{rl}|A|+|B|& :=|A\cup B|\\ |A|\cdot |B|& :=|A\times B|\\ |A{|}^{|B|}& :=|A^B|\end{array}$$ Dabei steht $\cup$ für vereinigt mit, $\times$ meint das kartesische Produkt, also die Menge aller geordneten Paare $(a,b)$, und $A^B$ meint die Menge aller Funktionen von $B$ nach $A$, also die Menge aller Teilmengen von $B\times A$, bei denen jeweils jedem $b\in B$ eindeutig ein $a\in A$ zugeordnet ist (siehe Kapitel 4.2).

Bei endlichen Mengen kann man die ersten beiden Regeln direkt nachvollziehen. Die dritte Regel ist da etwas komplizierter, aber man kann sie auch verstehen: Fügt man in der Menge $B$ ein neues Element hinzu, so ergeben sich $|A|$ Möglichkeiten, diesem neuen Element ein Element von $A$ zuzuordnen, d.h. die Zahl der Funktionen von $B$ nach $A$ ver-$|A|$-facht sich. Bei unendlichen Mengen sind die obigen Regeln als Definitionen für die linke Seite aufzufassen. Man kann zeigen, dass sie dann die üblichen Rechengesetze erfüllen.

Ein Beispiel: $A$ soll eine unendliche Menge sein, $B$ dagegen eine Menge mit nur einem Element, also $|B|=1$. Dann ergeben die obigen Regeln: $$|A|+1=|A\cup B|=|A|$$ denn die Mächtigkeit der unendlichen Menge $A$ ändert sich nicht, wenn nur ein Element hinzukommt. Analog ist es bei jeder endlichen Menge $B$. Daher kann man bei Kardinalzahlen nicht weiterzählen, anders als bei Ordinalzahlen!

Mit dem Auswahlaxiom kann man für die Kardinalzahlen unendlicher Mengen zeigen: $$|A|+|B|=|A|\cdot |B|=max(|A|,|B|)$$ Offenbar gewinnt die Menge mit der größeren Mächtigkeit, so dass eine weniger oder gleich mächtige Menge weder bei der Vereinigung noch bei der Paarbildung diese Mächtigkeit weiter erhöhen kann. Das müsste man natürlich noch im Detail nachweisen, wofür man dann wohl das Auswahlaxiom braucht. Wir verzichten hier darauf. Auf jeden Fall folgt, dass bei unendlichen Mengen $$|A|+|A|=|A|\cdot |A|=|A|$$ ist. Daher kann man bei unendlichen Mengen weder eine Subtraktion noch eine Division von Kardinalzahlen sinnvoll definieren.

Ein Beispiel für die Regel $|A|\cdot |A|=|A\times A|=|A|$ bildet die Menge $\mathbb{Q}$ der rationalen Zahlen (Brüche). Jeden Bruch $a/b$ kann man nämlich als Zahlenpaar $(a,b)$ aus $\mathbb{N}\times \mathbb{N}$ auffassen, und die Brüche und damit die Zahlenpaare kann man Eins-zu-Eins den natürlichen Zahlen zuordnen (siehe oben). Damit ist $$|\mathbb{Q}|=|\mathbb{N}\times \mathbb{N}|=|\mathbb{N}|\cdot |\mathbb{N}|=|\mathbb{N}|$$ d.h. $\mathbb{Q}$ und $\mathbb{N}$ haben dieselbe Mächtigkeit.

Nun sind wir gerüstet, uns noch einmal den Unterschied zwischen Kardinalzahlen und den Ordinalzahlen aus Kapitel 4.6 anzusehen. Ordinalzahlen werden dadurch definiert, dass man den Prozess des Zählens über die Gesamtmenge $\mathbb{N}$ der natürlichen Zahlen hinaus formal weiterführt. Dazu definiert man Ordinalzahlen ganz allgemein so: Jede Ordinalzahl ist die Menge aller kleineren Ordinalzahlen, wobei man mit der leeren Menge $\varnothing$ anfängt. Die ersten Ordinalzahlen sind also einfach die natürlichen Zahlen in der Mengendarstellung: $$\begin{array}{rl}0& :=\varnothing \\ 1& :=\{0\}\\ 2& :=\{0,1\}\\ 3& :=\{0,1,2\}\\ & ...\end{array}$$ Entsprechend ist $$\omega :=\mathbb{N}:=\{1,2,3,...\}$$ dann die Menge all dieser Mengen und damit die erste unendliche Ordinalzahl, wobei die Elemente der Größe nach geordnet sind. Aber es geht noch weiter: Man kann die Ordinalzahl $$\omega +1:=\{1,2,3,...,\omega \}$$ definieren, die ein größtes Element besitzt, das in $\mathbb{N}$ nicht vorkommt, nämlich die Menge $\mathbb{N}=\omega$ selbst. In diesem Sinn ist $\omega +1$ um Eins größer als die Menge $\omega =\mathbb{N}$, denn sie ist der Nachfolger von $\omega$. Dennoch weisen beide Mengen dieselbe Mächtigkeit (Kardinalzahl) auf, denn man kann eine Eins-zu-Eins-Abbildung zwischen $\omega$ und $\omega +1$ definieren. Dazu schreiben wir links die Elemente von $\omega +1$ und rechts die Elemente von $\omega$ auf und beginnen links mit dem Element $\mathbb{N}$, das wir rechts dem Element $1$ zuordnen: $$\begin{array}{rl}\mathbb{N}& \leftrightarrow 1\\ 1& \leftrightarrow 2\\ 2& \leftrightarrow 3\\ & ...\end{array}$$ Offenbar gibt es sehr viele Ordinalzahlen, die dieselbe Mächtigkeit aufweisen, also abzählbare Mengen sind: $\omega ,\omega +1,\omega +2,...$ . Sogar die Ordinalzahl ${ϵ}_0$ ist noch eine abzählbare Menge. Letztlich gelangt man von einer Ordinalzahl, die ja eine wohlgeordnete Menge ist, zur Kardinalzahl, indem man die Ordnung der Menge vergisst. Im obigen Beispiel haben wir vergessen, dass $\mathbb{N}$ das größte Element von $\omega +1$ ist – wir stellen es durch die Eins-zu-Eins-Abbildung gleichsam an den Anfang.

Man geht oft so vor, dass man die kleinste Ordinalzahl mit einer bestimmten Mächtigkeit als Repräsentanten der Äquivalenzklasse nimmt, oder sie sogar einfach gleich der Kardinalzahl setzt. Das muss dann immer eine Ordinalzahl ohne direkten Vorgänger sein, denn ein solcher Vorgänger hätte dieselbe Mächtigkeit. Ohne Auswahlaxiom geht das übrigens nicht, da man dann nicht mehr jede Menge wohlordnen kann und sie damit keine Ordinalzahl mehr besitzt. Ohne Auswahlaxiom ist es auch nicht mehr möglich, beliebige Kardinalzahlen in ihrer Größe miteinander zu vergleichen, also bei beliebigen Mengen zu sagen, welche von beiden die Mächtigere ist oder ob sie gleich mächtig sind – aber das nur am Rande, denn wir wollen das Auswahlaxiom hier voraussetzen.

Gibt es eine größte Kardinalzahl, also eine mächtigste Sorte von Mengen? Schauen wir uns dazu die Potenzmenge einer Menge $A$ an, also die Menge aller Teilmengen von $A$, wobei auch die leere Menge sowie die Menge $A$ selbst dazugehören.

Aus Kapitel 4.2 wissen wir: Wenn $A$ endlich ist und $n$ Elemente enthält, so enthält ihre Potenzmenge $2^n$ Elemente. Die Kardinalzahl dieser endlichen Potenzmenge wäre also $2^n$. Verallgemeinern wir dies auf unendliche Mengen, so müsste die Kardinalzahl der Potenzmenge gleich $2^{|A|}=|2^A|$ sein, also gleich die Kardinalzahl der Menge aller Funktionen von $A$ nach $\{0,1\}$ sein. Tatsächlich entspricht jeder solchen Funktion genau eine Teilmenge von $A$, denn wir können den Funktionswert $0$ oder $1$ für jedes Element von $A$ so interpretieren, dass er angibt, ob das Element zur Teilmenge dazugehört oder nicht. Halten wir fest:

Kardinalzahl der Potenzmenge: Die Potenzmenge einer Menge $A$ hat die Kardinalzahl $2^{|A|}$.

Nun kann man nach dem Potenzmengenaxiom (siehe Kapitel 4.2 ) zu jeder Menge $A$ die Potenzmenge bilden. Zu jeder Kardinalzahl $|A|$ gibt es also auch eine Kardinalzahl $2^{|A|}$, nämlich die der Potenzmenge. Mit Cantors Diagonalverfahren kann man nun leicht zeigen, dass es auch bei unendlichen Mengen keine Eins-zu Eins-Zuordnung zwischen $A$ und deren Potenzmenge gibt – es bleiben immer unendlich viele Elemente der Potenzmenge übrig. Daher ist die Potenzmenge von $A$ immer mächtiger als $A$ selbst. Es gibt also keine größte Kardinalzahl, also keine mächtigste Menge.

Kommen wir noch einmal zur Kontinuumshypothese. Die reellen Zahlen haben dieselbe Mächtigkeit wie die Potenzmenge von $\mathbb{N}$, denn man kann jede reelle Zahl durch eine endliche oder unendliche Teilmenge der natürlichen Zahlen kodieren (siehe Kapitel 4.2 ). Das kann man beispielsweise über die Binärdarstellung der reellen Zahl tun, indem man einfach alle Binärpositionsnummern, die eine 1 aufweisen, zusammennimmt – so gehört zur Binärzahl $0,1011$ die Menge $\{1,3,4\}$, und zu $0,11111...$ die Menge $\{1,2,3,...\}=\mathbb{N}$. Für die Vorkommastellen kann man sich eine ähnliche Strategie ausdenken (so könnte man mit geraden und ungeraden natürlichen Zahlen arbeiten, um Vor- und Nachkommastellen unterschiedlich zu kodieren). Es ist also $$|\mathbb{R}|=2^{|\mathbb{N}|}$$ und wir können die Kontinuumshypothese so schreiben:

Kontinuumshypothese: Es gibt keine Kardinalzahlen zwischen $|\mathbb{N}|$ und $2^{|\mathbb{N}|}$.

Das kann man auch auf beliebige unendliche Mengen $A$ verallgemeinern:

verallgemeinerte Kontinuumshypothese: Es gibt keine unendlichen Kardinalzahlen zwischen $|A|$ und $2^{|A|}$.

Es gibt also nach der Hypothese keine Menge, die in ihrer Mächtigkeit zwischen jeder beliebigen unendlichen Menge $A$ und ihrer Potenzmenge liegt. Diese Hypothese ist unabhängig von den ZFC-Axiomen der Mengenlehre, wie wir wissen, ist also weder beweisbar noch widerlegbar.

Unendliche Kardinalzahlen

Welche Kardinalzahlen gibt es? Zunächst haben wir natürlich die Kardinalzahlen endlicher Mengen, also die natürlichen Zahlen. Die nächstgrößere Mächtigkeit haben dann die abzählbar unendlichen Mengen. Ihre Kardinalzahl ist $|\mathbb{N}|$. Häufig benutzt man statt $|\mathbb{N}|$ auch die Bezeichnung

     

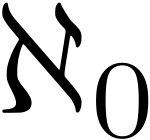
also den hebräischen Buchstaben $\mathrm{\aleph }$ (Aleph) mit Index Null. Es ist also $${\mathrm{\aleph }}_0:=|\mathbb{N}|$$ die Mächtigkeit (Kardinalzahl) der abzählbaren unendlichen Mengen. Sie ist zugleich die kleinste unendliche (transfinite) Kardinalzahl.

Nun haben wir gerade gelernt, dass es immer größere Kardinalzahlen gibt, und man kann sie sogar der Größe nach ordnen (Auswahlaxiom vorausgesetzt). Dabei gibt es zu jeder Kardinalzahl einen nächstgrößeren Nachfolger, aber wie bei den Ordinalzahlen hat nicht jede Kardinalzahl einen nächstkleineren Vorgänger (warum, kommt gleich). Daher kann man sie nicht mit natürlichen Zahlen komplett der Größe nach durchnummerieren, sondern nur mit Ordinalzahlen, wobei jede Ordinalzahl beim Durchnummerieren gebraucht wird: $${\mathrm{\aleph }}_0,{\mathrm{\aleph }}_1,{\mathrm{\aleph }}_2,...{\mathrm{\aleph }}_{\omega },{\mathrm{\aleph }}_{\omega +1},...$$ Die erste unendliche Kardinalzahl ${\mathrm{\aleph }}_0$ kennen wir: es ist $|\mathbb{N}|$, also die Mächtigkeit der abzählbaren Mengen. Was ist dann ${\mathrm{\aleph }}_1$, also die nächstgrößere Mächtigkeit von Mengen? Das hängt von der Kontinuumshypothese ab. Sie behauptet:

• Kontinuumshypothese: $${\mathrm{\aleph }}_1=|\mathbb{R}|=2^{{\mathrm{\aleph }}_0}$$

Die Kontinuumshypothese behauptet also, dass die nächstgrößere Mächtigkeit nach den natürlichen Zahlen die reellen Zahlen sind. Wie wir wissen, ist diese Behauptung in der ZFC-Mengenlehre unentscheidbar. Die ZFC-Axiome sagen zwar, dass man die Kardinalzahlen ordnen kann, sagen aber schon bei der zweiten unendlichen Kardinalzahl nicht mehr, ob diese der Mächtigkeit der reellen Zahlen entspricht. Moderne Entwicklungen in der Mengenlehre legen oft ${\mathrm{\aleph }}_2=|\mathbb{R}|$ nahe (siehe unten), d.h. es liegt noch eine Mächtigkeit zwischen den natürlichen und den reellen Zahlen. Denkbar sind aber sogar Modelle mit beispielsweise ${\mathrm{\aleph }}_3=|\mathbb{R}|$.

Ähnlich ist es wegen der verallgemeinerte Kontinuumshypothese auch bei anderen Kardinalzahlen. Es ist also aufgrund der ZFC-Axiome nicht allgemein entscheidbar, ob die Nachfolger-Kardinalzahl durch Bilden der Potenzmenge erreicht werden kann oder nicht. Dazu legen die ZFC-Axiome den Mengenbegriff nicht hinreichend genau fest. Potenzmengenbildung und Nachfolger-Kardinalzahlen bilden in der ZFC-Mengenlehre zunächst einfach nur zwei verschiedene Konzepte, zu größeren Mächtigkeiten zu gelangen, ohne dass festliegt, wie beide Konzepte miteinander verbunden sind. Geht man von der Gültigkeit der verallgemeinerten Kontinuumshypothese aus, so ist die Nachfolger-Kardinalzahl ${\mathrm{\aleph }}_{\alpha +1}$ einer unendlichen Kardinalzahl ${\mathrm{\aleph }}_{\alpha }$ gleich $2^{{\mathrm{\aleph }}_{\alpha }}$.

Was aber ist dann ${\mathrm{\aleph }}_1$, wenn man sich nicht auf die Kontinuumshypothese stützen möchte? Nun, es ist die nächstgrößere Mächtigkeit von Mengen – welche auch immer das genau ist. Hier gibt es nur sehr abstrakte Definitionen wie beispielsweise die folgende von Cantor, die sich auf Ordinalzahlen stützt (siehe beispielsweise Peter Ripota: Von aleph-null zu aleph-eins):

• Betrachten wir alle abzählbaren unendlich großen Ordinalzahlen $\{\omega ,\omega +1,...,{ϵ}_0,...\}$, dann ergibt sich so eine Menge, deren Mächtigkeit gleich ${\mathrm{\aleph }}_1$ ist.

• ${\mathrm{\aleph }}_1$ ist die erste schwer erreichbare Kardinalzahl nach ${\mathrm{\aleph }}_0$.

Leicht erreichbare (singuläre) und schwer erreichbare (reguläre) Kardinalzahlen: Eine unendliche Kardinalzahl $\kappa$ nennt man leicht erreichbar (nicht regulär, singulär), wenn man sie als Vereinigungsmenge $$\kappa ={\cup }_{i\in I}{X}_i$$ darstellen kann, wobei die Indexmenge $I$ und die Mengen $X_i$ weniger mächtig als $\kappa$ sind. Mengen kleinerer Mächtigkeit reichen also aus, um eine leicht erreichbare Kardinalzahl zu erzeugen. Geht diese Darstellung nicht (weil beispielsweise die Indexmenge $I$ oder ein $X_i$ genauso mächtig wie $\kappa$ sein muss), so bezeichnet man $\kappa$ als schwer erreichbar (regulär). Eine leicht erreichbare Kardinalzahl kann man also als weniger mächtige Vereinigung weniger mächtiger Mengen schreiben, eine schwer erreichbare nicht. Man sagt auch, man kann eine schwer erreichbare Kardinalzahl $\kappa$ nicht mit weniger als $\kappa$ Schritten erreichen.

Eine unendliche Potenzmenge wäre beispielsweise schwer erreichbar. Die Begriffe singulär und regulär sind historisch bedingt und laufen manchmal Intuition zuwider – ich versuche daher, sie hier weitgehend zu vermeiden.

Schon die erste unendliche Kardinalzahl ${\mathrm{\aleph }}_0$ ist demnach schwer erreichbar (regulär). Man kann sie nämlich nur durch $${\mathrm{\aleph }}_0={\cup }_{n\in \mathbb{N}}n=\mathbb{N}$$ darstellen, d.h. die Indexmenge $I$ ist hier gleich $\mathbb{N}$ und ist somit genauso mächtig wie die dargestellte Kardinalzahl ${\mathrm{\aleph }}_0$. Man braucht abzählbar unendlich viele endliche Mengen, um eine abzählbar unendliche Mächtigkeit zu erzeugen. Also ist eine Voraussetzung für leichte Erreichbarkeit nicht erfüllt.

Analog ist es mit ${\mathrm{\aleph }}_1$: man braucht überabzählbar viele abzählbare Mengen, so dass die Indexmenge $I$ wieder dieselbe Mächtigkeit wie die dargestellte Kardinalzahl hat. Generell kann man zeigen, dass jede unendliche Nachfolger-Kardinalzahl schwer erreichbar (regulär) ist. Daher kommt auch die Motivation für den Begriff regulär. Allerdings muss nicht umgekehrt jede schwer erreichbare Kardinalzahl eine Nachfolger-Kardinalzahl sein (siehe unten).

Von ${\mathrm{\aleph }}_1$ aus geht es nun immer weiter: ${\mathrm{\aleph }}_2$, ${\mathrm{\aleph }}_3$, ${\mathrm{\aleph }}_4$, ... . Richtig greifbar sind diese Mächtigkeiten nur mit der verallgemeinerten Kontinuumshypothese, denn dann entsteht die nächste Mächtigkeit immer durch Potenzmengenbildung. Wie bei den Ordinalzahlen gibt es aber auch eine Mächtigkeit, die größer ist als ${\mathrm{\aleph }}_2$, ${\mathrm{\aleph }}_3$, ${\mathrm{\aleph }}_4$, ... , also größer ist als alle ${\mathrm{\aleph }}_n$ mit $n\in \mathbb{N}$. Das ist dann unser ${\mathrm{\aleph }}_{\omega }$, das wir oben in der Liste bereits gesehen haben. Diese Mächtigkeit lässt sich mit endlich vielen Potenzmengen-Schritten nicht erreichen. Man bezeichnet eine Kardinalzahl wie ${\mathrm{\aleph }}_{\omega }$ auch als Limeskardinalzahl. Durch Nachfolger-Schritte oder beliebig oft wiederholte Potenzmengenbildung kann man eine Limeskardinalzahl nicht erreichen:

Limeskardinalzahl: Eine Limeskardinalzahl ist eine Kardinalzahl ohne nächstkleineren Vorgänger. Für eine Limeskardinalzahl $\kappa$ gilt also: Wenn eine Kardinalzahl $\alpha$ kleiner als $\kappa$ ist, so ist auch deren Nachfolger kleiner als $\kappa$.

Wie kann man aber nun eine Limeskardinalzahl erreichen? Zumindest bei der ersten Limeskardinalzahl ${\mathrm{\aleph }}_{\omega }$ weiß man es: Man kann Sie erreichen, indem man die Vereinigungsmenge aller kleineren Kardinalzahlen bildet: $${\mathrm{\aleph }}_{\omega }={\cup }_{n\in \mathbb{N}}{\mathrm{\aleph }}_n$$

Das ist ganz analog zu den Grenz-Ordinalzahlen aus Kapitel 4.6. Die Kardinalzahl ${\mathrm{\aleph }}_{\omega }$ ist demnach leicht erreichbar (nicht regulär, singulär), denn hier genügt als Indexmenge die Menge $\mathbb{N}$, und die ist wie auch alle ${\mathrm{\aleph }}_n$ weniger mächtig als ${\mathrm{\aleph }}_{\omega }$. Die Motivation für den Begriff singulär wird hier sichtbar: die Nachfolger-Bildung reicht nicht, um die Zahl zu erreichen, und man muss eine Art Sprung machen.

Bleibt die Frage, ob auch größere Limeskardinalzahlen leicht erreichbar sind, also durch Bilden der Vereinigungsmenge aller kleineren Kardinalzahlen mit kleinerer Indexmenge erreichbar sind. Das ist tatsächlich normalerweise der Fall (nämlich dann, wenn sich die Existenz der Limeskardinalzahl in ZFC beweisen lässt, siehe unten). Dennoch könnte man fragen:

• Welches ist die kleinste schwer erreichbare Limeskardinalzahl ?

Diese harmlos aussehende Frage hat es in sich, wie wir noch sehen werden. Eine solche Limeskardinalzahl muss irgendwie eine unglaublich gigantische Mächtigkeit von Mengen repräsentieren, wenn weder Nachfolgerschritte (Potenzmengenbildung) noch die Bildung der Vereinigungsmenge aller bisherigen Schritte diese Mächtigkeit erzeugen können. Wie soll man dann an eine solche Kardinalzahl überhaupt noch herankommen? Tatsächlich stellt sich heraus, dass sich die Existenz solcher Kardinalzahlen in ZFC werder beweisen noch widerlegen lässt – sie liegen außerhalb der Reichweite der ZFC-Axiome. Mehr dazu etwas weiter unten beim Thema unerreichbare Kardinalzahl.

Jede Kardinalzahl ist zugleich auch eine Ordinalzahl (Auswahlaxiom vorausgesetzt), wobei man üblicherweise immer die kleinste aller gleich mächtigen Ordinalzahlen nimmt. So hat Cantor beispielsweise ${\mathrm{\aleph }}_1$ definiert (siehe oben). Da viele Ordinalzahlen gleich mächtige Mengen sind, ist die nächstgrößere Kardinalzahl normalerweise nicht gleich der nächsten Ordinalzahl. Die Kardinalzahlen bilden also eine Unterklasse der Ordinalzahlen.

Ohne Auswahlaxiom ist die Lage komplizierter, da man dann nicht mehr jede Menge wohlordnen und ihr eine Ordinalzahl zuordnen kann. Entsprechend gibt es dann Kardinalzahlen, die keine Ordinalzahl sind, da man die entsprechenden Mengen nicht wohlordnen kann. Man kann dann nicht immer sagen, welches die größere Kardinalzahl ist, also welches die mächtigere Menge ist. Wir hatten das oben bereits erwähnt. In diesem Kapitel wollen wir aber das Auswahlaxiom allgemein voraussetzen, also ZFC statt nur ZF betrachten.

Unerreichbare Kardinalzahlen

Die obige Grafik zeigt, wie es nach ${\mathrm{\aleph }}_{\omega }$ weitergeht: Es folgt ${\mathrm{\aleph }}_{\omega +1}$ usw. bis ${\mathrm{\aleph }}_{\omega +\omega }$. Alle Ordinalzahlen sind als Index möglich! Wir können uns viele Zwischenschritte sparen, wenn wir nur die Index-Ordinalzahlen betrachten, die zugleich eine Kardinalzahl darstellen. Die erste wäre dann ${\mathrm{\aleph }}_{\omega }={\mathrm{\aleph }}_{{\mathrm{\aleph }}_0}$. Noch viel größer wäre dann ${\mathrm{\aleph }}_{{\mathrm{\aleph }}_1}$. Oder gar ${\mathrm{\aleph }}_{{\mathrm{\aleph }}_{\omega }}={\mathrm{\aleph }}_{{\mathrm{\aleph }}_{{\mathrm{\aleph }}_0}}$. Und so kann man den Index immer größer machen, und dessen Index ebenfalls immer größer machen und so fort. Im Grenzfall ensteht so eine unendliche Folge von einem Index mit einem Index mit einem Index .... . Man nimmt einfach die aktuelle Kardinalzahl immer wieder als Position (Index) der nächsten Kardinalzahl. So startet man mit ${\mathrm{\aleph }}_0$, nimmt dann die Kardinalzahl an dieser Position, also ${\mathrm{\aleph }}_{{\mathrm{\aleph }}_0}$, und dann als nächstes ${\mathrm{\aleph }}_{{\mathrm{\aleph }}_{{\mathrm{\aleph }}_0}}$ und so weiter. Dieses Wachstum kann nur dann theoretisch aufhören, wenn man irgendwann eine Position (nennen wir sie $\theta$ ) erreicht, an der zugleich die Kardinalzahl $\theta$ steht: $$\theta ={\mathrm{\aleph }}_{\theta }$$ (siehe z.B. Peter Ripota: Von aleph-null zu aleph-eins sowie Mario Sedlak: Große Kardinalzahlen). Man sagt auch, $\theta$ hat eine Fixpunkteigenschaft. Die Position der Zahl $\theta$, die ja normalerweise eigentlich kleiner als $\theta$ sein müsste, verschmilzt in den Tiefen der Unendlichkeit mit der Zahl selbst und hat sie dort auf geheimnisvolle Weise eingeholt!

Ich muss zugeben, dass meine Intuition hier langsam versagt. Man kann das Ganze sogar noch weiter treiben: Irgendwie hat man dabei immer ein Werkzeug, das einen bis zu einer Mächtigkeit – nennen wir sie $\alpha$ – gebracht hat und das man nun $\alpha$-mal anwendet, was einen zur Mächtigkeit ${\alpha }^{\prime }$ bringt, so dass man das Werkzeug nun ${\alpha }^{\prime }$-mal anwenden kann und so fort.

Wenn man dann das Werkzeug nach unendlicher Iteration ausgereizt hat, fordert man die Existenz eines neuen Werkzeuges, indem man sagt, dass dieses neue Werkzeug die Grenzen des alten Werkzeuges überwinden kann. Auch dieses neue Werkzeug kann man nun iterieren, und zwar immer bis zu der Mächtigkeit, die es einem bisher geliefert hat.

Tja, und dann fordert man schließlich wieder ein neues Werkzeug, das alle bisherigen Grenzen sprengt. Außerdem ist auch dieses Werkzeug-Erfinden eine Art Iteration, die man auf die Spitze treiben kann. Und so geht es immer weiter. Wichtig ist, dass man immer wieder eine neue Idee braucht, die über alle bisherigen Iterationen hinausgeht. Anders gesagt: Prinzipiell neue Mächtigkeiten erfordern offenbar neue Axiome!

In diesem Sinne (neue Axiome) kann man auch generell über (ggf. noch größere) "unerreichbare" Kardinalzahlen (also Mächtigkeiten von Mengen) nachdenken, die man überhaupt nicht mehr explizit angeben kann. So sind sie definiert:

unerreichbare Kardinalzahl: $\kappa$ ist eine unerreichbare Kardinalzahl genau dann, wenn sie eine überabzählbare schwer erreichbare Limeskardinalzahl ist. Das bedeutet im Detail (siehe oben): $\kappa$ ist überabzählbar: $\kappa >{\mathrm{\aleph }}_0$ $\kappa$ ist schwer erreichbar (regulär): Man kann sie nicht als Vereinigungsmenge ${\cup }_{i\in I}{X}_i$ darstellen, wobei die Indexmenge $I$ und die Mengen $X_i$ weniger mächtig als $\kappa$ sein müssen. Kurz: Man braucht Mengen der Mächtigkeit $\kappa$, um zu $\kappa$ zu gelangen. $\kappa$ ist eine Limeskardinalzahl: Sie hat keinen nächstkleineren Vorgänger und kann demnach auch nicht durch Potenzmengenbildung erreicht werden: Wenn $\mu <\kappa$ ist, so muss auch $2^{\mu }<\kappa$ sein,

Das sind im Grunde drei Negativaussagen, die klarmachen, wie man nicht zu einer unerreichbaren Kardinalzahl kommen kann – weshalb sie eben auch unerreichbar ist.

Aber wie kann man ergründen, ob es solche Kardinalzahlen überhaupt gibt?

Die ZFC-Mengenlehre gibt auf diese Frage keine eindeutige Antwort. Sie sagt, solche Kardinalzahlen sind denkbar, aber auch ihr Fehlen ist denkbar. Man kann mit den Mitteln der ZFC-Mengenlehre nicht entscheiden, ob es sie gibt.

Das bringt uns zurück zu folgender Frage: Warum ist die ZFC-Mengenlehre nicht mächtig genug, um die Existenz einer oder gar mehrerer unerreichbaren Kardinalzahlen zu entscheiden?

Eine anschauliche Begründung wäre: Weder die Potenzmengenbildung noch eine weniger mächtige Vereinigung weniger mächtiger Mengen reichen aus, um die Mächtigkeit einer unerreichbaren Kardinalzahl zu erzeugen. Damit hat die ZFC-Mengenlehre aber keine Werkzeuge mehr, um diese Mächtigkeit gleichsam von unten zu konstruieren. Es bleibt also nichts anderes übrig, als die Existenz entsprechend mächtiger Mengen explizit zuzulassen oder abzulehnen – beide Alternativen sind möglich.

Eine andere Begründung ergibt sich, wenn man sich Modelle der ZFC-Mengenlehre in der Hierarchie aller Mengen anschaut. Wir werden nämlich gleich herausfinden, dass die Hierarchiestufe Nummer $\kappa$ in dieser Mengenhierarchie genau dann ein Modell der ZFC-Mengenlehre ist, wenn $\kappa$ eine unerreichbare Kardinalzahl ist, also eine überabzählbare schwer erreichbare Limeskardinalzahl. Wir sehen: unerreichbare Kardinalzahl können durchaus wichtig werden!

Da ZFC nun nicht seine eigene Widerspruchsfreiheit beweisen kann, kann es auch nicht beweisen, dass es eine Hierarchiestufe Nummer $\kappa$ gibt, die ein Modell von ZFC ist. Damit kann ZFC auch nicht beweisen, dass die unerreichbare Kardinalzahl $\kappa$ existiert, denn sonst wäre diese Hierarchiestufe ja ein Modell. Schauen wir uns die Details dazu an:

Das Mengenuniversum V

Wie kann man die Welt aller denkbaren Mengen systematisch von unten nach oben aufbauen? Man fängt mit der einfachsten Menge an, also mit der leeren Menge. Und dann baut immer neue Hierarchiestufen auf, indem man die Potenzmenge der Vorgängerstufe bildet, also die Menge aller Teilmengen inklusive der leeren Menge (wobei auch die komplette Menge der Vorgängerstufe als Teilmenge zählt, also als Element in der Potenzmenge vorkommt). Auf diese Weise entsteht eine Hierarchie von immer mächtigeren Mengen, die man auch als von-Neumann-Universum bezeichnet und mit dem Buchstaben $V$ abkürzt. Schauen wir uns das konkret an, wobei wir überall da, wo es geht, die Mengen als natürliche Zahlen schreiben (siehe die Mengendarstellung natürlicher Zahlen oben sowie in Kapitel 4.6 ): $$\begin{array}{rl}\mathrm{S}\mathrm{t}\mathrm{u}\mathrm{f}\mathrm{e}0:V_0& :=\varnothing =0\\ \mathrm{S}\mathrm{t}\mathrm{u}\mathrm{f}\mathrm{e}1:V_1& :=\{0\}=1\\ \mathrm{S}\mathrm{t}\mathrm{u}\mathrm{f}\mathrm{e}2:V_2& :=\{0,1\}=2\\ \mathrm{S}\mathrm{t}\mathrm{u}\mathrm{f}\mathrm{e}3:V_3& :=\{0,1,2,\{1\}\}\\ & ...\end{array}$$

Man sieht, wie es immer komplexer wird. Die Zahl der Mengen (Elemente) nimmt exponentiell zu. Insbesondere sind in der Menge der Stufe $n$ immer alle natürlichen Zahlen bis $n-1$ als Elemente enthalten. Allerdings erhält man so nie eine Menge $\mathbb{N}$, die alle natürlichen Zahlen umfasst. Daher führen wir nach abzählbar unendlich vielen Stufen die Stufe $\omega$ ein, in der wir die Vereinigungsmenge aller Vorgängermengen bilden:

Stufe $\omega$:   $V_{\omega }:={\cup }_n{V}_n$   =   Vereinigungsmenge aller Vorgängermengen $V_n$

Dabei läuft $n$ über alle natürlichen Zahlen. Diese Menge enthält alle natürlichen Zahlen, und sogar noch viel mehr – letztlich ist $V_{\omega }$ die Menge aller endliche Mengen. Dabei ist $V_{\omega }$ selbst bereits eine unendliche Menge. Um andere unendliche Mengen wie die aller natürlichen Zahlen zu gewinnen, müssen wir die nächste Stufe erklimmen, also die Potenzmenge bilden. Diese enthält dann alle endlichen oder unendlichen Mengen mit beliebigen Elementen aus $V_{\omega }$.

Stufe $\omega +1$:   $V_{\omega +1}:=\mathcal{P}(V_{\omega })$   =   Menge aller Teilmengen von $V_{\omega }$

Eine der Mengen in $V_{\omega +1}$ ist die Menge $\mathbb{N}$ der natürlichen Zahlen. Aber es kommen auch alle endlichen sowie unendlichen Teilmengen der natürlichen Zahlen darin vor, beispielsweise die Menge der geraden Zahken oder die Menge der Primzahlen. Und so geht es immer weiter. Nach unendlich vielen Einzelschritten mit Potenzmengenbildung folgt dabei immer ein großer Vereinigungsschritt, mit dem man die nächste Ordinalzahl ohne Vorgänger erreicht, beispielsweise $V_{\omega +\omega }$. Dieses $V_{\omega +\omega }$ enthält alle Mengen, die man in der üblichen Mathematik normalerweise so braucht. Alle ZFC-Axiome bis auf das Ersetzungsaxiom sind in $V_{\omega +\omega }$ erfüllt – mehr dazu weiter unten.

Und so geht es immer weiter, wobei der Index schrittweise alle Ordinalzahlen durchläuft. Übrigens: Falls der Eindruck entsteht, dass bei $V_{\omega }$ ein anderes Bildungsgesetz als bei $V_n$ angewendet wird – dem ist nicht so. Das allgemeine Bildungsgesetz für jede Ordinalzahl $\alpha$ lautet:

Stufe $\alpha$:   $V_{\alpha }:={\cup }_{\beta <\alpha }\mathcal{P}(V_{\beta })$   =   Vereinigungsmenge der Potenzmengen aller Vorstufen Vβ

d.h. $V_{\alpha }$ besteht aus allen Mengen, die man in weniger als $\alpha$ Schritten aufbauen kann, wobei man in jedem Schritt die Objekte verwendet, die man im Schritt zuvor erzeugt hat.

Ganz am Schluss bildet man dann die große Vereinigungsklasse $V$, die formal die komplette Mengenhierarchie umfasst (von-Neumann-Universum):

$$V:={\cup }_{\alpha }{V}_{\alpha }$$

Allerdings ist $V$ eine Klasse und keine Menge mehr, im Gegensatz zu jeder Zwischenstufe $V_{\alpha }$ , die alle für sich Mengen sind. Wir wissen ja, dass man mit der Menge aller Mengen Probleme bekommt. Man kann zeigen, dass $V$ alle Mengen umfasst, die es in der ZFC-Mengenlehre gibt – unsere Mengenhierarchie hat also keine Mengen übersehen. Genauer gilt: Zu jeder Menge in ZFC gibt es eine Stufe $V_{\alpha }$ in der Hierarchie, die die Menge enthält. Das folgt aus dem Regularitätsaxiom (Fundierungsaxiom) und der Tatsache, dass jede Stufe $V_{\alpha }$ transitiv ist, d.h. jedes Element der Stufe ist zugleich auch eine Teilmenge der Stufe (siehe beispielsweise John R. Steel: What is a Woodin Cardinal, Notices of the AMS, Vol 54, No. 9, S. 1146, October 2007).

Auch wenn diese Hierarchie schrittweise erzeugt wurde und erst einmal einen ganz soliden Eindruck macht, so muss man sich dennoch klarmachen, dass man es hier mit keiner einfachen Hierarchie nach dem Muster   1, 2, 3, 4, ...   zu tun hat, sondern mit einer Hierarchie nach dem Muster   1, 2, 3, 4, ... , ω, ω+1, ...   , bei der mit   "..."   unendlich viele Schritte abgekürzt werden, und dies unendlich oft – eben so, wie man mit Ordinalzahlen zählt. Man spricht von einer transfiniten Rekursion, ganz analog zur transfiniten Induktion aus Kapitel 4.6. Dabei entstehen Mengen von beliebig großer Komplexität und Mächtigkeit, je weiter man geht. Immerhin genügt ja bereits ein einziger Potenzmengen-Schritt, um aus einer abzählbar unendlichen Menge eine überabzählbare zu machen. Im nächsten Schritt entstehen dann alle Teilmengen der überabzählbaren Menge. Von den reellen Zahlen her wissen wir, dass es sehr komplexe Teilmengen der reellen Zahlen gibt, also wahre mathematische Monster. Was geschieht dann erst bei der transfiniten Rekursion dieses Potenzmengen-Schrittes! Irgendwann werden sich daher die Grenzen der ZFC-Axiome zeigen, denn sie werden diese Komplexitäten nicht beliebig weit erfassen können. Die ZFC-Axiome erlauben es nicht, das Gesamtuniversum $V$ zu definieren, auch wenn das oben formal vielleicht so aussieht: $V$ ist keine Menge mehr.

Das Mengenuniversum $V$ repräsentiert mathematisch so etwas wie das absolut Unendliche, denn es umfasst nach heutigem Wissen alle denkbaren mathematischen Objekte. Die folgende etwas unpräzise Idee über das absolut Unendliche bezeichnet man als Reflexionsprinzip (Reflection Principle):

Reflexionsprinzip: Das absolut Unendliche ist unbeschreibbar, kann also nicht durch eine Eigenschaft charakterisiert werden, die es von anderen Dingen unterscheidet. Insbesondere kann das absolut Unendliche nicht das einzige Objekt sein, das eine bestimmte Eigenschaft aufweist, denn dann wäre es ja durch diese Eigenschaft charakterisierbar. Jede Eigenschaft, die wir dem absolut Unendlichen zuschreiben, muss also auch einem anderen Objekt zukommen.

Bezogen auf das Mengenuniversum $V$ bedeutet das (siehe wieder John R. Steel: What is a Woodin Cardinal, Notices of the AMS, Vol 54, No. 9, S. 1146, October 2007):

Reflexionsprinzip in der Mengenlehre: Wenn wir dem Mengenuniversum $V$ eine bestimmte Eigenschaft zuschreiben, so gibt es irgendwelche Hierarchiestufen $V_{\alpha }$, denen diese Eigenschaft ebenfalls zukommt.

Wenn wir beispielsweise sagen, dass $V$ unendlich ist, dann gibt es irgendwelche $V_{\alpha }$, die ebenfalls unendlich sind. Die Axiome der Mengenlehre garantieren, dass das erfüllt ist.

Und wenn wir sagen, $V$ ist ein Modell der ZFC-Mengenlehre, dann muss es eine Stufe $\kappa$ in der Mengenhierarchie geben, so dass bereits $V_{\kappa }$ ein Modell der ZFC-Mengenlehre ist. Was ein solches Modell ist, haben wir in Kapitel 4.4 gesehen: Die ZFC-Axiome müssen für alle Mengen in der Modelldomäne wahr sein und es darf keine Menge fehlen, deren Existenz man mit den Axiomen beweisen kann (und umgekehrt). Generell sind nach Gödels Vollständigkeitssatz alle mit ZFC beweisbaren Aussagen im Modell wahr. Es muss aber nicht jede in dem Modell wahre Aussage auch in ZFC beweisbar sein – das ist dann Gödels Unvollständigkeitssatz. Eine Aussage ist genau dann in ZFC beweisbar, wenn sie in jedem Modell von ZFC wahr ist.

Ist das Reflexionsprinzip zuverlässig? Kann man in ZFC beweisen, dass es eine solche Stufe $\kappa$ in der Mengenhierarchie gibt, so dass $V_{\kappa }$ ein Modell der ZFC-Mengenlehre ist (also insbesondere alle Mengen enthält, deren Existenz sich in ZFC beweisen lässt)? Da aus der Existenz eines Modells der ZFC-Mengenlehre deren Widerspruchsfreiheit folgt, würde das bedeuten, dass die ZFC-Mengenlehre damit ihre eigene Widerspruchsfreiheit bewiesen hätte – das kann sie nach Gödel aber prinzipiell nicht. Also kann sie auch nicht die Existenz der Modellstufe $\kappa$ beweisen. (siehe Kapitel 4.4 ). Übrigens ist auch die Voraussetzung, dass $V$ ein Modell ist, wackelig – intuitiv liegt das zwar nahe, denn $V$ enthält ja irgendwie alles, was in der Mengenlehre denkbar ist, aber beweisen kann man das nicht, denn $V$ ist ja noch nicht einmal eine Menge.

Immerhin legt das Reflexionsprinzip aber nahe, dass Modellstufen $V_{\kappa }$ von ZFC eine sinnvolle Denkmöglichkeit sind, auch wenn ZFC ihre Existenz nicht beweisen kann. So sind die meisten ZFC-Axiome bereits in den unteren Stufen der Mengenhierarchie erfüllt. Beispielsweise ist das Unendlichkeitsaxiom in der Stufe $V_{\omega +1}$ erfüllt, da diese Stufe bereits unendliche Mengen enthält (siehe oben). Das Potenzmengenaxiom ist für jede Stufe $V_{\alpha }$ erfüllt, bei der $\alpha$ eine Limeszahl ist, also eine Ordinalzahl ohne Vorgänger.

Man kann sich überlegen dass alle ZFC-Axiome bis auf Eines in $V_{\omega +\omega }$ erfüllt sind. Dieses eine problematische Axiom ist das Ersetzungsaxiom, das folgendes behauptet (siehe Kapitel 4.2 ): Das Abbild einer beliebigen Menge unter einer Abbildung $F$ ist wieder eine Menge. Man kann leicht eine Abbildung konstruieren, die aus $V_{\omega +\omega }$ hinausführt, beispielsweise indem man jede gerade Zahl $2n$ auf $\omega +n$ abbildet (siehe auch A. Shenitzer und J. Steprans: The Evolution of Integration, The American Mathematical Monthly, January 1994, Vol 101, No. 1, pp. 66-72). Erst bei einer Stufe $V_{\kappa }$ mit einer überabzählbaren schwer erreichbaren Limeskardinalzahl $\kappa$ kann man alle Abbildungen $F$ einfangen, so dass $V_{\kappa }$ ein Modell von ZFC wird. Da ZFC die Existenz eines Modells seiner selbst weder beweisen noch widerlegen kann, kann ZFC auch die Existenz von $\kappa$ nicht entscheiden, wie der Begriff unerreichbar ja auch sagt. Damit ist die Existenz dieser Stufe aber immerhin denkbar, führt also zu keinen (neuen) Widersprüchen. Und schon sind wir beim Thema Erweiterungen der ZFC-Mengenlehre!

Erweiterungen der ZFC-Mengenlehre

Niemand hindert uns daran, die Existenz von Mengen mit gewissen unerreichbaren Mächtigkeiten $\kappa$ einfach zu fordern – wie beispielsweise die Existenz von $\theta$ weiter oben. Das ist eigentlich nichts Ungewöhnliches, denn die ZFC-Mengenlehre macht auch nichts anderes: Sie fordert über das Unendlichkeitsaxiom und das Potenzmengenaxiom ebenfalls gewissen Unendlichkeiten (siehe Kapitel 4.2 ). Offenbar sind aber noch weitere Unendlichkeiten im Mengenuniversum denkbar, die damit nicht erfasst werden. Warum sollten wir auf diese Unendlichkeiten verzichten? Wir können sie bei Bedarf durch geeignete neue Axiome mit hinzunehmen und so die ZFC-Mengenlehre erweitern! Die Ausdruckskraft der Mengenlehre wird dadurch verbessert, denn sie kann nun auch über Mächtigkeiten von Mengen sprechen, die zu gigantisch für ZFC waren. Gödel hoffte, dass man durch solche Axiome vielleicht eine Erweiterung der Mengenlehre schaffen könnte, die die Kontinuumshypothese entscheiden würde. Insbesondere hoffte er, dass man die Komplexität eines möglichen Gegenbeispiels zur Kontinuumshypothese auf diese Weise irgendwie einfangen und genauer spezifizieren könnte (wenn man es schon nicht konstruieren kann, wie Gödel gezeigt hatte). Da die Kontinuumshypothese in ZFC unentscheidbar ist, muss die Komplexität eines Gegenbeispiels ja jenseits der Ausdruckskraft von ZFC sein.

Wie man heute weiß, lässt sich Gödels Idee so leider nicht durchführen. Man konnte mit Hilfe vom Modellerweiterungen (Forcing-Methode) zeigen, dass große Kardinalzahlen die Kontinuumshypothese nicht entscheiden können. Die Kontinuumshypothese ist also eine Nummer zu schwer für unerreichbare Kardinalzahlen.

Andererseits ist die ZFC-Mengenlehre nach heutigem Wissen vermutlich stark genug, um alle natürlicherweise in der Zahlentheorie auftretenden Fragen über natürliche Zahlen entscheiden zu können. Man sagt, ZFC scheint bezüglich natürlicher arithmetischer Aussagen vollständig zu sein. Mit natürlich meint man Probleme, die man nicht extra als unabhängig von der ZFC-Mengenlehre konstruiert hat, sondern die man ohne Rücksicht auf die Mengenlehre in der üblichen Zahlentheorie untersucht. Gibt es vielleicht natürliche Aussagen, die in ihrer Komplexität zwischen den typischen zahlentheoretischen Problemen und der Kontinuumshypothese liegen? In ZFC alleine wären diese Aussagen dann unentscheidbar, aber die Hinzunahmen geeigneter unerreichbarer Kardinalzahlen würden sie vielleicht entscheidbar machen.

Solche Aussagen gibt es! Schauen wir uns zum Vergleich noch einmal die Kontinuumshypothese an: Sie behauptet, dass es eine Teilmenge der reellen Zahlen mit einer bestimmten einfachen Eigenschaft gibt. Diese Frage nach einer Teilmenge der reellen Zahlen macht die Aussage so komplex, denn Teilmengen der reellen Zahlen können wahre mathematische Monster sein. Weniger komplex sind Aussagen der Form es gibt reelle Zahlen x, so dass ... oder für alle reellen Zahlen x gilt: ... . So etwas nennt man projektive Aussagen. Bei projektiven Aussagen muss jeder in der Aussage vorkommende Quantor auf die reellen Zahlen beschränkt sein, darf also nicht nach Teilmengen der reellen Zahlen fragen, so wie es die Kontinuumshypothese tut. Man kann auch sagen, dass projektive Aussagen aus Sicht der reellen Zahlen von erster Ordnung sind.

Über eine projektive Ausage kann man eine projektive Mengen definieren, nämlich einfach die Menge aller reellen Zahlen, für die die projektive Aussage gilt. So bilden beispielsweise die rationalen Zahlen eine projektive Menge. Auch ein Intervall zwischen zwei reellen Zahlen ist eine projektive Menge. Letztlich sind alle reellen Zahlenmengen, die man als Mathematiker so im täglichen Leben braucht, projektive Mengen. Nicht-projektive Mengen treten eher als pathologische mathematische Monster auf, beispielsweise beim Banach-Tarski-Paradoxon, bei dem man per Auswahlaxiom eine Vollkugel vom Volumen 1 punktweise in vier Punktwolken zerlegt, die man dann über Verschiebungen und Drehungen zu zwei Vollkugeln mit zusammen doppeltem Volumen zusammensetzen kann. Die vier Punktwolken sind Beispiele für solche pathologischen unanschaulichen Mengen. Insbesondere sind sie nicht-Lebesque-messbare Mengen, d.h. sie haben kein Volumen.

Es wäre nun wünschenswert, wenn alle natürlicherweise auftretenden Aussagen über projektive Mengen in der ZFC-Mengenlehre entschieden werden könnten, also eindeutig wahr oder falsch wären. Das ist leider zunächst nicht der Fall. Man stellt aber empirisch fest, dass sie alle gleichwertig sind zu Aussagen über die Existenz gewisser unerreichbarer Kardinalzahlen. Die Erfahrung zeigt also: Die typischen Fragen über alltägliche (also projektive) reelle Zahlenmengen sind gleichwertig zu Aussagen über die Mächtigkeit von Mengen, die zu groß für die ZFC-Mengenlehre sind. Man kann also große Kardinalzahlen dazu verwenden, die natürlichen Aussagen über projektive Mengen nach der Mächtigkeit der Kardinalzahlen zu ordnen. Besonders wichtig ist dabei das folgende Ergebnis aus dem Jahr 1988 (was Woodin-Kardinalzahlen sind, kommt etwas später):

Projektive Determiniertheit (PD) und Woodin-Kardinalzahlen: Wenn es unendlich viele unerreichbare Woodin-Kardinalzahlen gibt, so ist jede projektive Menge determiniert, d.h. es gilt projektive Determiniertheit (PD). Fordert man umgekehrt, dass jede projektive Menge determiniert ist, so folgt die Existenz der Woodin-Kardinalzahlen.

Projektive Mengen haben viele wünschenswerte Eigenschaften, wenn sie determiniert sind. So sind sie beispielsweise Lebesque-messbar, d.h. nicht-messbare Monstermengen wie beim Banach-Tarski-Paradoxon sind für projektive Mengen ausgeschlossen. Das Auswahlaxiom wäre für projektive Mengen damit weitgehend entschärft – es wird für diese Mengen praktisch nicht mehr benötigt. Man geht heute davon aus, dass man die ZFC-Mengenlehre möglichst so erweitern sollte, dass projektive Mengen determiniert sind (mehr dazu weiter unten).

Von oben wissen wir, dass es unter determinierten Mengen kein Gegenbeispiel zur Kontinuumshypothese gibt. Wenn also jede projektive Menge determiniert ist, dann kann es unter ihnen kein Gegenbeispiel zur Kontinuumshypothese mehr geben. Projektive Aussagen über reelle Zahlen können also dann keine reellen Zahlenmengen erzeugen, deren Mächtigkeit zwischen den natürlichen und den reellen Zahlen liegt.

Natürlich kann man reelle Zahlenmengen definieren, die komplizierter als die projektiven Mengen sind. Auch bei diesen Mengen kann man zeigen, dass die Existenz von bestimmten unerreichbaren Kardinalzahlen gleichwertig zur Determiniertheit dieser Mengen ist, so dass damit allzu schlimme mathematische Monstermengen verhindert werden. Je komplizierter die Menge ist, umso größer müssen die geforderten Kardinalzahlen sein, um Determiniertheit sicherzustellen.

Wie definiert man eigentlich solche unerreichbaren Kardinalzahlen wie beispielsweise die Woodin-Zahlen? Im Wesentlichen benutzt man sogenannte elementare Einbettungen $$j:V\to M$$ die einen Bezug zwischen unserem Mengenuniversum $V$ und einem (möglicherweise kleineren) Mengenuniversum $M$ herstellt. Man sagt auch, $M$ ist eine hinreichend robuste transitive Unterklasse des Gesamtuniversums $V$. Dabei soll $j$ alle Relationen zwischen Mengen erhalten – wenn also beispielsweise $A$ Untermenge von $B$ ist, so muss auch $j(A)$ Untermenge von $j(B)$ sein. Und natürlich soll $j$ nicht einfach die identische Abbildung sein, d.h. sie muss auch irgendetwas verändern. Insbesondere soll sie auch bestimmte Ordinalzahlen verändern. Im Grunde lotet $j$ die Freiheiten aus, die man bei der Festlegung des Mengenuniversums noch hat. Wenn man nun mit Hilfe von $j$ bestimmte unerreichbare Kardinalzahlen definiert, so sind diese umso größer (stärker), je ähnlicher die beiden Mengenuniversen $M$ und $V$ werden. Je größer die unerreichbaren Kardinalzahlen werden, umso genauer legen sie also die Struktur des Mengenuniversums fest. Das legt nahe, dass große Kardinalzahlen eine sinnvolle Erweiterung der ZFC-Axiome sind, denn ZFC alleine legt das Mengenuniversum $V$ und damit $j$ nicht allzu weit fest, wie wir wissen.

Optimal wäre es natürlich, denn $V=M$ wäre, d.h. wenn es eine elementare Einbettung $j$ von $V$ nach $V$ gäbe. Dann wäre das Mengenuniversum festgelegt. Man spricht hier vom Wholeness-Axiom. Aber wir ahnen es schon, dass das wohl nicht möglich sein wird, denn es wäre ja so etwas wie die Definition des absolut Unendlichen.

Damit sind wir nun gerüstet für die Definition der Woodin-Kardinalzahlen – nur, damit man sie mal gesehen hat und ein Gefühl für die Komplexität solcher Definitionen bekommt (mehr dazu siehe wieder John R. Steel: What is a Woodin Cardinal, Notices of the AMS, Vol 54, No. 9, S. 1146, October 2007):

Woodin-Kardinalzahlen: Eine Kardinalzahl $\delta$ ist eine Woodin-Kardinalzahl, wenn die folgende Bedingung erfüllt ist: Für alle Teilmengen $A$ der entsprechenden Mengenhierarchiestufe $V_{\delta }$ muss es eine kleinere Kardinalzahl $\kappa <\delta$ geben, die $A$-stark in $\delta$ ist (d.h. $\kappa$ ändert sich, obwohl sich alle nieder-hierarchischen Anteile von $A$ nicht ändern). Genauer bedeutet das: Für alle kleineren Kardinalzahlen $\beta <\delta$ muss es eine elementare Einbettungen $j$ geben, so dass $A$ und $j(A)$ dieselbe Schnittmenge mit $V_{\beta }$ haben und so, dass $\kappa$ ein kritischer Punkt von $j$ ist, d.h. $\kappa$ ist die kleinste Kardinalzahl, die von $j$ nicht mehr auf sich selbst abgebildet wird. Es gilt sogar $\kappa <j(\kappa )$.

Kann man das verstehen? Versuchen wir es: Wir schauen uns die Hierarchiestufe $V_{\delta }$ zur Woodin-Kardinalzahl $\delta$ an und greifen uns irgendeine beliebig große Teilmenge $A$ davon heraus (sie darf auch gleich $V_{\delta }$ sein). Von dieser Teilmenge $A$ schauen wir uns dann irgendeinen tieferliegenden Anteil an, nämlich die Schnittmenge mit einer niedrigeren Hierarchiestufe $V_{\beta }$ . Wir können nun dazu immer eine Einbettung $j$ hinbekommen, die diesen tieferliegenden Anteil nicht ändert, egal wie nahe wir mit $\beta$ an $\delta$ heranrücken oder wie groß wir $A$ machen. In diesem Sinn ist fast ganz $V_{\delta }$ als Mengenuniversum festgelegt – den nicht festgelegten Teil können wir beliebig schrumpfen lassen, indem wir mit $\beta$ an $\delta$ heranrücken, aber er verschwindet nie ganz. Trotzdem aber tut diese Abbildung $j$ unterhalb der Woodin-Mächtigkeit $\delta$ etwas, denn dort soll es eine Mächtigkeit $\kappa$ geben, die durch $j$ vergrößert wird. Zugegeben, das ist recht abstrakt, aber es geht hier ja auch um abstrakte Fragen zu komplexen Unendlichkeiten. Unmittelbar einsichtig als naheliegendes Axiom scheint das allerdings nicht zu sein. Es sind vielmehr die Auswirkungen, die hier zählen. Es war daher ein hartes Stück Arbeit, Woodin-Kardinalzahlen als eine mögliche sinnvolle Ergänzung zu ZFC herauszustellen.

Wie hängt das Ganze nun mit der Wahrheit von projektiven Aussagen über die reellen Zahlen zusammen? Nehmen wir dazu an, ein $V_{\alpha }$ ist ein Modell der ZFC-Mengenlehre – so ein Modell brauchen wir ja, um den Wahrheitsbegriff zu definieren. Genauer ist es sogar so, dass $V_{\alpha }$ eine hinreichend elementare abzählbare Substruktur enthalten muss, die ein transitives Modell von ZFC ist (siehe Kapitel 4.4 ). Insbesondere enthält das Modell dann die obige Mengendarstellung der natürlichen Zahlen. Wir wollen nun dieses Modell erweitern (Forcing). Dabei kommen keine neuen natürlichen Zahlen hinzu, d.h. die Wahrheit von Aussagen über natürliche Zahlen ändert sich durch die Erweiterung nicht. Was aber geschieht mit Aussagen über reelle Zahlen? Immerhin starten wir ja mit einem abzählbaren Modell, so dass durch die Erweiterung neue reelle Zahlen hinzukommen können.

Es zeigt sich, dass die Wahrheit von bestimmten projektiven Aussagen über reelle Zahlen sich durch die Erweiterung nicht ändert. Diese Aussagen haben die Form

• Es gibt eine reelle Zahl $x$ , so dass für alle reellen $y$ die arithmetische Aussage $A(x,y)$ gilt.

Solche Aussagen merken also von neu hinzukommenden reellen Zahlen offenbar nichts. Das kann bei komplizierteren projektiven Aussagen über reelle Zahlen aber im Prinzip anders sein – es müssen nur hinreichend komplexe mathematische Monstermengen aus reellen Zahlen hinzukommen.

Man kann erreichen, dass sich die Wahrheit von allen projektiven Aussagen über reelle Zahlen durch eine Modellerweiterung nicht ändert (man sagt dann, das Modell ist projektiv absolut). Die Methode dazu kennen wir bereits: Wir fordern, dass sowohl das Modell $V_{\alpha }$ als auch seine Erweiterungen unendlich viele Woodin-Kardinalzahlen enthalten. Das sind dann keine Modelle von ZFC allein mehr, sondern Modelle einer erweiterten Version der Mengenlehre, die ein Zusatzaxiom erfüllt – nämlich die Existenz von Woodin-Kardinalzahlen. In dieser erweiterten Mengenlehre ist der Begriff der reellen Zahlen also umfassender festgelegt als in der ZFC-Mengenlehre, denn die Wahrheit von projektiven Aussagen über reelle Zahlen ändert sich nicht bei Modellerweiterungen. Man spricht auch von Stabilisierung dieses Teils des Mengenuniversums – ein wichtiges Kriterium bei der Suche nach neuen Axiomen zur Erweiterung von ZFC.

Es liegt nun nahe, dass man sich ein möglichst kleines Modell als Startpunkt aussuchen sollte, welches aber alle reellen Zahlen sowie unendlich viele Woodin-Kardinalzahlen enthält. Die Wahrheit von projektiven Aussagen über reelle Zahlen ändert sich dann beim Erweitern des Modells nicht. Die über diese Aussagen definierten projektiven reellen Zahlenmengen sind dann determiniert, verhalten sich also einigermaßen gesittet. Die Erfahrung zeigt, dass die Wahrheit aller natürlicherweise auftretenden projektiven Aussagen über reelle Zahlen dann festliegt. In diesem Sinn gelingt es mit Hilfe der Woodin-Kardinalzahlen und der dazu gleichwertigen projektiven Determiniertheit, die Eigenschaften der reellen Zahlen weitgehend einzufangen – zumindest was projektive Aussagen betrifft. Man sagt auch, die projektive Determiniertheit ist für projektive Mengen empirisch vollständig.

Nun ist die Kontinuumshypothese leider keine projektive Aussage – sie ist komplexer, denn sie spricht nicht direkt über reelle Zahlen, sondern sie verneint die Existenz einer bestimmten Teilmenge der reellen Zahlen. Die Woodin-Kardinalzahlen sorgen dann zumindest schon einmal dafür, dass keine projektive Aussage über reelle Zahlen ein Gegenbeispiel zur Kontinuumshypothese erzeugen kann (siehe oben). Aber es könnte ja immer noch kompliziertere reelle Zahlenmengen geben, deren Mächtigkeit zwischen den natürlichen und den reellen Zahlen liegt. Die Woodin-Kardinalzahlen verbieten das nicht.

Wie komplex ist denn die Kontinuumshypothese? Zum Vergleich: Arithmetische Aussagen sprechen über natürliche Zahlen (enthalten aber keine Quantoren über Teilmengen der natürlichen Zahlen). Die nächste Stufe sind die projektiven Aussagen – sie sprechen über reelle Zahlen (enthalten aber keine Quantoren über Teilmengen der reellen Zahlen). Da man reelle Zahlen auch als Teilmengen der natürlichen Zahlen auffassen kann, sprechen projektive Aussagen auch über Teilmengen der natürlichen Zahlen $\mathbb{N}={\mathrm{\aleph }}_0$. Damit ist klar: Die nächste Stufe (bezogen auf die Mächtigkeit der Mengen) sind dann Aussagen, die über Teilmengen von ${\mathrm{\aleph }}_1$ sprechen (wobei wir nicht ${\mathrm{\aleph }}_1=\mathbb{R}$ setzen, da wir neutral bleiben wollen, was die Kontinuumshypothese betrifft). Die Kontinuumshypothese kann nun genau so formuliert werden, fällt also in diese Komplexitätsklasse.

Bei Aussagen dieser Komplexität können wir nicht dasselbe erreichen wie bei den projektiven Aussagen. Große Kardinalzahlen können nicht verhindern, dass der Wahrheitswert dieser Aussagen in verschiedenen Modellerweiterungen unterschiedlich sein kann (siehe Gödels Idee weiter oben). Was also ist zu tun? Nun, man könnte sich auf diejenigen Modellerweiterungen beschränken, die den Wahrheitswert dieser Aussagen unverändert lassen. Man kann zeigen, dass das genau diejenigen Modellerweiterungen sind, bei denen jede sogenannte stationäre (d.h. in gewissem Sinn dicke) Menge bei der Erweiterung stationär bleibt. Man spricht vom Bounded Martin's Maximum.

Und nun sind wir ganz weit vorne an der Front der Forschung: Im Jahr 2002 konnte Todorcevic zeigen, dass bei dieser Einschränkung der möglichen Modellerweiterungen die Kontinuumshypothese in diesen Modellen falsch ist, und dass man in gewissem Sinn eine Menge definieren kann, deren Mächtigkeit zwischen den natürlichen und den reellen Zahlen liegt. Die Formulierung in Ralf Schindler: Wozu brauchen wir große Kardinalzahlen? lautet etwa so:

• Es existiert eine Bijektion $f:\mathbb{R}\to {\mathrm{\aleph }}_2$, so dass die Menge $\{(x,y)\in \mathbb{R}\times \mathbb{R},f(x)\le f(y)\}$ definierbar ist mit Mächtigkeit ${\mathrm{\aleph }}_1$.

Was wollen uns diese Worte sagen? Die Bijektion $f$ bedeutet, dass die Menge der reellen Zahlen die Mächtigkeit ${\mathrm{\aleph }}_2$ hat, so dass nach den natürlichen Zahlen ${\mathrm{\aleph }}_0$ noch Platz für die Mächtigkeit ${\mathrm{\aleph }}_1$ ist. Eine solche Menge mit Mächtigkeit ${\mathrm{\aleph }}_1$ wird dann als Punktmenge in der reellen Ebene angegeben. Sie enthält alle die Punkte $(x,y)$, bei denen der $x$-Koordinate über die Bijektion $f$ eine kleinere oder gleich große Ordinalzahl aus ${\mathrm{\aleph }}_2$ zugeordnet ist als der $y$-Koodinate. Zugegeben, das ist ziemlich abstrakt, und $f$ wird auch nicht konkret angegeben. Aber viel konkreter kann ein solches Gegenbeispiel auch gar nicht sein (projektive Aussagen gehen ja nicht; mehr dazu auch im nächsten Kapitel).

Bisher hatte jede Zusatzforderung an die ZFC-Mengenlehre üblicherweise dazu geführt, dass die Kontinuumshypothese stimmte. Die Zusatzforderungen wirkten sich wie Restriktionen aus, die die Komplexität von Mengen soweit beschränkten, dass kein Gegenbeispiel mehr möglich war. Nun ist es dagegen gelungen, durch Zusatzforderungen solche Modelle herauszufiltern, in denen es mindestens ein Gegenbeispiel gibt, das sogar halbwegs konkret ist.

Was hat die obige Einschränkung der Modellerweiterungen mit unerreichbaren Kardinalzahlen zu tun? Nun, man kann offenbar zeigen, dass sich auch einige offene Fragen bei unerreichbaren Kardinalzahlen so klären lassen. Und nicht nur solche Fragen – auch viele weitere interessante Aussagen werden entschieden. Übrigens kann man unsere obige Forderung nach Woodin-Kardinalzahlen problemlos hinzunehmen, so dass dann wieder alle projektiven Mengen determiniert sind und auch alle natürlichen projektiven Aussagen entschieden werden. Das ergibt dann eine umfassende und aussagekräftige Theorie, in der viele Aussagen entschieden werden, ohne dass dies einfach nur durch Ausschluss komplizierter Mengen geschieht. Diese Theorie sagt dann, dass ein Gegenbeispiel zur Kontinuumshypothese nicht durch eine projektive Aussage über reelle Zahlen entstehen kann, findet aber dennoch einen Weg, ein Gegenbeispiel zu definieren.

Auch andere moderne Erweiterungen der ZFC-Mengenlehre mit möglichst großer Aussagekraft führen zu ähnlichen Resultaten. Es sieht also heute so aus, als ob die Kontinuumshypothese besser falsch sein sollte. Das bedeutet, dass Modelle, in denen sie wahr ist, eher einen einschränkenden Charakter haben, während Modelle, in denen sie falsch ist, mehr Raum für kompliziertere Konstrukte lassen. Bei dieser Argumentation darf man aber nie vergessen: Die Kontinuumshypothese ist im Rahmen der ZFC-Mengenlehre nicht an-sich wahr oder falsch. Sie ist denkbar, und auch ihr Gegenteil ist denkbar. Eine mathematische Denkwelt, in der sie nicht gilt, scheint aber möglicherweise reichhaltiger zu sein als eine, in der sie gilt. Ob man diesen Reichtum gebrauchen kann, ist momentan noch offen. Vielleicht braucht man ihn, um beispielsweise das P=?NP-Problem zu lösen (siehe Kapitel 5.1)?! Auch aus der theoretischen Physik sind viele Beispiele bekannt, bei denen zuvor scheinbar rein abtrakte mathematische Begriffe plötzlich Nutzen gestiftet haben – man denke an die Differentialgeometrie, die das zentrale Werkzeug der allgemeinen Relativitätstheorie geworden ist, oder an den unendlichdimensionalen Hilbertraum, den man in der Quantentheorie braucht. Die Natur wird eben auch immer abstrakter, je tiefer man in ihre Strukturen vordringt!

Die Untersuchungen zu möglichen und sinnvollen Erweiterungen der ZFC-Mengenlehre sind ein sehr aktives Forschungsgebiet. Immer wieder gibt es dort neue Einsichten. Einen guten Überblick liefert beispielsweise der Artikel Unendlichkeiten – Wie viele reelle Zahlen gibt es? von Natalie Wolchover in Spektrum der Wissenschaft, Januar 2022 (siehe auch Quantamagazine: How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer). Dort wird beschrieben, wie man mit der Methode des Forcings – eine Art geschickte Intervallschachtelung – immer wieder neue reelle Zahlen konstruieren kann, die zuvor noch nicht in dem verwendeten reellen Modell des Zahlenstrahls vorhanden waren. So kann man das Kontinuum immer wieder erweitern. Mit erweiterten Forcing-Methoden kann man sogar die wildesten Mengenuniversen schaffen – ein Multiversum mehrdeutiger mathematischer Wirklichkeiten.

Ganz so wild und vieldeutig möchte man es dann doch nicht haben. Also versucht man, das Forcing mit geeigneten Zusatzaxiomen zu ZFC sinnvoll einzudämmen. Martins Maximum gehört dazu und war zeitweise sehr beliebt (siehe auch weiter oben). Die Kontinuumshypothese ist dann falsch, d.h. es liegt eine überabzählbare Menge zwischen den natürliche und den reellen Zahlen.

Eine andere Möglichkeit ist Woodins Axiom (*) (ausgesprochen: "Stern") – so genannt, weil es wie eine helle Lichtquelle erschien. Es erweitert die ZF-Axiome (ohne das Auswahlaxiom C) plus dem Axiom der Determiniertheit AD. Mit (*) kann man Aussagen über Eigenschaften von Mengen treffen, beispielsweise: "Für alle Mengen von ${\mathrm{\aleph }}_1$ reellen Zahlen (das ist die erste nicht-abzählbare Unendlichkeit) gibt es weitere reelle Zahlen, die nicht in diesen Mengen enthalten sind." Das Kontinuum aller reellen Zahlen ist also größer als die erste nicht-abzählbare Unendlichkeit ${\mathrm{\aleph }}_1$ und die Kontinuumshypothese demnach falsch.

Beide Axiome, Martins Maximum und Woodins (*) sehen vielversprechend und natürlich aus, sind aber wohl nicht kompatibel miteinander. Man muss sich also entscheiden, aber für welches? Es stellte sich dann aber heraus, dass man Martins Maximum leicht abwandeln kann (Martins Maximum++), sodass aus ihm Woodins (*) folgt. Das sieht schon mal gut aus.

Aber die Lage bleibt kompliziert, denn auch Woodins (*) kann man abwandeln zu (*)+, das etwas über die Menge aller reellen Teilmengen sagt, also ein sehr starkes Axiom ist. Leider widerspricht es Martins Maximum.

Die Lage bleibt also verworren. Noch hat sich kein neues Axiom herausgeschält, das als eindeutiger Favorit gelten kann, um die ZF-Axiome zu erweitern, ihre Aussagekraft zu stärken und so die mathematischen Wirklichkeiten (und insbesondere die Natur der reellen Zahlen) besser festzunageln, mit denen man arbeiten möchte. Ob es jemals ein solches Axiom als "natürliche Erweiterung" der ZF-Axiome geben wird, ist ungewiss, aber die Mathematikerinnen und Mathematiker, die sich mit diesem etwas exotischen Gebiet befassen, haben noch lange nicht aufgegeben.

Literatur:

• Wikipedia: Cardinal number und Wikipedia: Kardinalzahl (Mathematik)

• Wikipedia: Große Kardinalzahl

• Wikipedia: Von Neumann universe

• Einen guten ersten Überblick für Einsteiger findet man hier: Lexikon des Unendlichen

• Ralf Schindler: Wozu brauchen wir große Kardinalzahlen?, Mathematische Semesterberichte 53 (2006), pp. 65 - 80
  – gibt einen guten Überblick zu dem Thema inklusive Erklärung der wesentlichen Grundbegriffe. Dieser Text diente teilweise als Leitfaden für das vorliegende Kapitel.

• Peter Ripota: Von aleph-null zu aleph-eins und andere Kapitel vom selben Autor.

• John R. Steel: What is a Woodin Cardinal, Notices of the AMS, Vol 54, No. 9, S. 1146, October 2007

• W. Hugh Woodin: The Continuum Hypothesis, Part I, Notices of the AMS, Vol 48, No. 6, S. 567, June/July 2001

• A. Shenitzer und J. Steprans: The Evolution of Integration, The American Mathematical Monthly, January 1994, Vol 101, No. 1, pp. 66-72

• Jean-Paul Delahaye: Wie real ist das Unendliche?, Spektrum der Wissenschaft, März 2009, S.54

• Natalie Wolchover: Unendlichkeiten – Wie viele reelle Zahlen gibt es?, Spektrum der Wissenschaft, Januar 2022 (siehe auch Quantamagazine: How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer).

• Mario Sedlak: Große Kardinalzahlen

• Mario Sedlak: Unerreichbare Kardinalzahlen